Типовая задача 7
Исследовать функцию у = 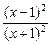 и построить ее график.
и построить ее график.
Решение. 1. Так как функция не определена при х + 1 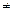 0 (х
0 (х 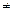 –1), то D(y) =
–1), то D(y) = 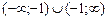 .
.
Функция является ни четной, ни нечетной, так как D(y) не является симметричной относительно начала координат.
Функция является непериодической.
Находим асимптоты.
х = –1 — точка разрыва. Если х будет стремиться к (–1) слева, оставаясь меньше (–1), то (х + 1)2 — положительная бесконечно малая функция, а 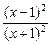 — положительная бесконечно большая функция, т. е. если
— положительная бесконечно большая функция, т. е. если 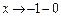 , то (х + 1)2
, то (х + 1)2 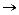 +0, а
+0, а 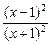
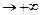 , или
, или 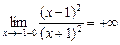 .
.
Аналогично показывается, что 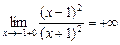 .
.
Делаем вывод, что прямая х = –1 — вертикальная асимптота
графика.
Для нахождения наклонных асимптот у = k · x + b при 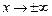
находим пределы:
k = 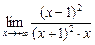 =
= 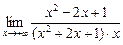 =
= 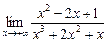 =
=
= 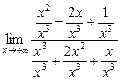 =
= 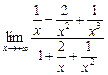 =
= 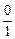 = 0,
= 0,
b = 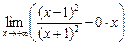 =
= 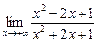 =
= 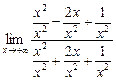 =
=
= 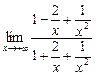 =
= 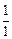 = 1.
= 1.
Таким образом, у = 1 — горизонтальная асимптота графика.
Аналогичным образом показывается, что у = 1 — горизонтальная асимптота и при х 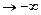 .
.
5. 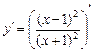 =
= 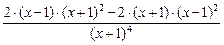 =
=
= 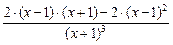 =
= 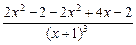 =
= 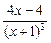 .
.
6. Находим критические точки. Решаем уравнение y' = 0:
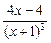 = 0
= 0 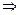
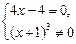
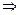
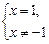
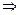 x = 1.
x = 1.
Точка х = –1, в которой производная не существует, не принадлежит D(y). Точка х = 1 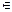 D(y). Поэтому х = 1 — единственная критическая точка.
D(y). Поэтому х = 1 — единственная критическая точка.
7. Критическая точка х = 1 разбивает область определения на интервалы. Определим знак первой производной у' на каждом интервале (рис. 14).
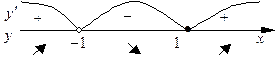
Рис. 14
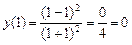 .
.
Составим следующую таблицу:
| х | (– 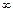 ; –1) ; –1)
| –1 | (–1; 1) | (1; 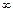 ) )
| |
| y' | + | Не существует | – | + | |
| у | Возрастает | Не существует | Убывает | Возрастает | |
| Экстремума нет | min |
8. 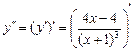 =
= 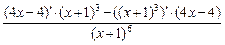 =
=
= 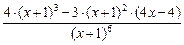 =
= 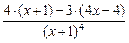 =
=
= 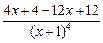 =
= 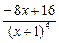 .
.
9. Решим уравнение 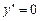 :
: 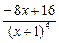 = 0.
= 0.
Отсюда 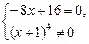
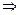
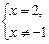
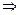 х = 2.
х = 2.
Точка х = –1, в которой вторая производная не существует, не принадлежит D(y). Точка х = 2 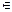 D(y). Определим знак второй производной на области определения (рис. 15).
D(y). Определим знак второй производной на области определения (рис. 15).
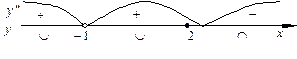
Рис. 15
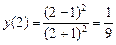 .
.
Составим следующую таблицу:
| х | (– 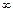 ; –1) ; –1)
| –1 | (–1; 2) | (2; 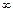 ) )
| |
| y'' | + | Не существует | + | – | |
| у | 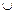
| Не существует | 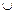
| 1/9 | 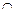
|
| График вогнутый | Перегиба нет | График вогнутый | Точка перегиба | График выпуклый |
10. Находим точки пересечения графика с осями координат.
10.1. С осью Ох. Так как у = 0, то имеем
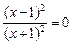
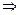
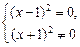
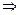
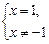
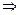 х = 1.
х = 1.
10.2. С осью Оу. Так как х = 0, то имеем у = 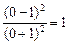 .
.
Значит, (1,0), (0,1) — точки пересечения с осями координат.
Так как числитель и знаменатель дроби 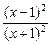 являются полными квадратами, то
являются полными квадратами, то 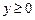 при всех х
при всех х 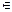 D(y).
D(y).
11. По результатам исследования строим график функции (рис. 16).
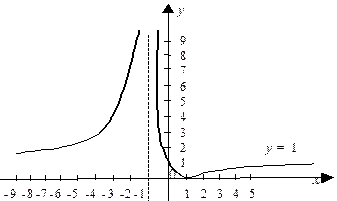
|
| Рис. 16 |
Дата добавления: 2014-12-02; просмотров: 827;
