Уравнение линии. Прямая на плоскости

Одним из важнейших в аналитической геометрии является вопрос об уравнении линии на плоскости.

Всякая линия есть множество точек плоскости, координаты которых должны быть связаны некоторым условием. Это условие записывается в виде уравнения.

Определение. Уравнение

F(х, у)=0

называется уравнением линии, если этому уравнению удовлетворяют координаты х и у любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки, не лежащей на этой линии.

В этом случае говорят: уравнение F(х, у)=0 определяет эту линию.

Пример № 4.

Показать, что уравнение

х²+у²=r²

определяет окружность.

Окружностью называется множество точек плоскости, расстояние каждой из которых до данной точки постоянно. Пусть М(х, у) – любая точка плоскости.

Расстояние этой точки от начала координат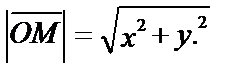

Тогда уравнению х²+у²=r² удовлетворяют только те точки, для которых 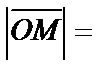r, т. е. точки, лежащие на окружности радиуса r с центром в начале координат. Если же точка не лежит на окружности, то расстояние 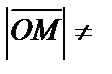r.

Итак, уравнению х²+у²=r² удовлетворяют координаты любой точки окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности. Значит, уравнение х²+у²=r² определяет окружность при любом r>0.

Очевидно, уравнение

(х-х₀)²+(у-у₀)²=r²

определяет окружность с центром в точке С(х₀, у₀) радиуса r>0.

Например, уравнение

х²+(у+1)²=1

определяет окружность радиуса r=1 с центром в точке С(0; -1).

Простейшей линией является прямая на плоскости. Рассмотрим различные виды уравнения прямой.

1. Уравнение прямой, проходящей через данную точку М₀(х₀,у₀) перпендикулярно данному вектору 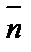= (А; В).

Чтобы вывести уравнение прямой, возьмем на ней любую точку М(х, у), которая может по прямой перемещаться.

В любом случае вектор 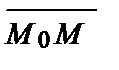, ограниченный данной точкой М₀(х₀,у₀) и произвольной точкой М(х, у), всегда лежит на прямой и поэтому перпендикулярен данному вектору 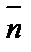(А; В). Найдем координаты вектора 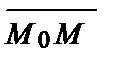и запишем условие перпендикулярности векторов 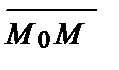и .

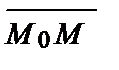^ ÞА × (х – х₀) + В × (у – у₀) = 0.

Полученному уравнению удовлетворяют координаты любой точки прямой и не могут удовлетворять координаты точки, не лежащей на прямой (тогда условие перпендикулярности не будет выполняться).

А × (х – х_о) + В × (у – у₀) = 0 (1)

– уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. Вектор 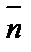(А; В) называют нормальным вектором.

В уравнении (1) раскроем скобки:

А × х + В × у + (–А × х₀ – В × у_о) = 0

Обозначим число – А × х₀ – В × у₀ = С. Уравнение прямой примет вид:

А × х + В × у + С = 0 (2)

Его называют общим уравнением прямой, а коэффициенты при х и у задают нормальный вектор .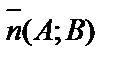

Заметим, что уравнение прямой – уравнение первой степени с двумя переменными. Поэтому в аналитической геометрии прямую линию называют линией первого порядка.

2. Уравнение прямой, проходящей через данную точку М₀(х₀, у₀) параллельно данному вектору 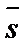=(m; n).

Пусть М(х, у) – любая точка прямой. Тогда векторы и всегда коллинеарны. Запишем условие коллинеарности векторов 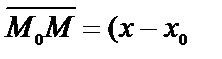; у–у₀) и 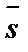=(m; n):

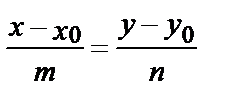(3)

уравнение прямой, параллельной вектору 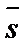=(m; n).

3. Уравнение прямой, проходящей через две данные точки М₁(х₁, у₁) и М₂(х₂, у₂)

Для любой точки М(х, у) прямой векторы =(х – х₁; у – у₁) и = (х₂ – х_1; у₂ –у₁) всегда коллинеарны, а потому

(4)

– искомое уравнение.

4. Уравнение прямой с угловым коэффициентом.

Выведем уравнение прямой, проходящей через точку М₀(х_0, у₀) под углом 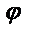к оси абсцисс Ох.

Угол 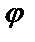между прямой и осью Ох называют углом наклона прямой, а угловым коэффициентом k прямой называют тангенс угла 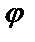наклона этой прямой, т. е. k =tg .

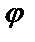Для любой точки М(х, у) прямой отношение равно 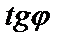, поэтому 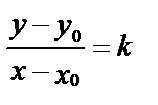или у–у₀=k×(х–х₀).

Получили уравнение прямой, проходящей через данную точку М₀(х₀, у₀) в заданном направлении

у–у₀ = k × (х–х₀) (5)

Здесь – угловой коэффициент прямой. Угол наклона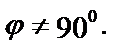

Если точка М₀ – точка пересечения прямой с осью ординат Оу, то ее координаты х₀= 0, у₀= b. Уравнение принимает вид: у–b=k×x, или

у = k × x + b (6)

– уравнение прямой с угловым коэффициентом, b – начальная ордината прямой.

5. Угол между прямыми

Пусть даны две прямые своими общими уравнениями:

А₁×х+В₁×у+С₁=0 и А₂×х+В₂×у+С₂=0

Так как 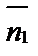= (А₁; В₁) и – нормальные векторы данных прямых, то угол 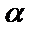между прямыми равен углу между нормальными векторами и .

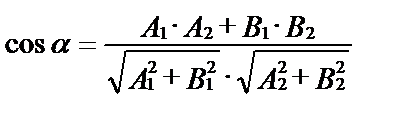Если две прямые заданы уравнениями с угловым коэффициентом: 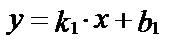и 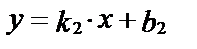, то угол 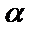между ними удобнее вычислять по формуле:

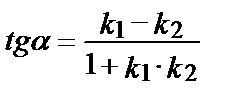
доказательство которой легко усматривается из рисунка:

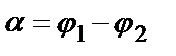
Если прямые перпендикулярны, то 1 + k₁ × k₂ = 0 и .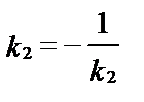

Если прямые параллельны, то

k₁ = k₂.

Пример № 5

Проверить, что четыре точки А(–2;–2), В(–3;1), С(7;7) и D(3;1) служат вершинами трапеции, и составить уравнение высоты, опущенной из вершины А.

В трапеции две стороны параллельны, а две – нет. Составим уравнения каждой из четырех сторон по формуле (4).

Уравнение АВ:

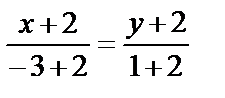или у+2=-3(х+2).

Уравнение ВС: ,

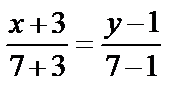или у–1= .

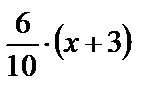Уравнение CD: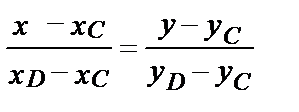

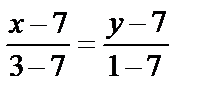или у–7= .

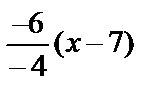Уравнение DА: ,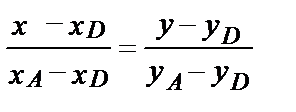

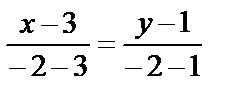или у-1= .

Сравним угловые коэффициенты полученных прямых; они равны для прямых ВС и DA: .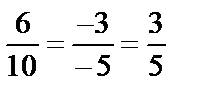

ВС и DA – основания трапеции, АВ и СD – боковые стороны ее.

Высота трапеции перпендикулярна основанию, и угловой коэффициент прямой, совпадающей с высотой, равен 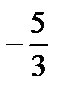. Составим уравнение прямой, проходящей через точку А(–2,–2) с угловым коэффициентом k= 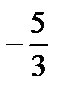по формуле (5):

у+2= 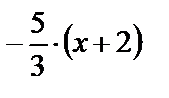или 5х+3у+16=0.

Построением убедимся в правильности решения.