Геометрический смысл линейных неравенств
Уравнение А×х+В×у+С=0 определяет на плоскости прямую, которая является границей двух полуплоскостей. Координаты любой точки одной полуплоскости удовлетворяют неравенству А×х+В×у+С>0, координаты любой точки другой – неравенству А×х+В×у+С<0.
Поэтому, чтобы решить, какая именно полуплоскость определяется неравенством А×х+В×у+С>0, например, следует подставить координаты конкретной точки в это неравенство. Если получите верное неравенство, то неравенство А×х+В×у+С>0 определяет ту полуплоскость, в которой лежит выбранная точка.
Например, решим, какую полуплоскость задает неравенство 2х-3у+6<0. Построим прямую 2х–3у+6=0 по точкам пересечения ее с осями координат.
| Построим полученные точки (-3;0) и (0;2) и прямую. |
у 0 2

Координаты точки О(0;0) не удовлетворяют неравенству 2х-3у+6<0.
Поэтому нужная полуплоскость не содержит точку О. Таким образом, неравенство 2х-3у+6<0 определяет полуплоскость, лежащую «выше» прямой (заштрихована).
Очевидно, полуплоскость, содержащая начало координат, определяется неравенством 2х-3у+6>0.
Пример № 6.
Построить множество точек, удовлетворяющих системе неравенств:
1) 
Построим две прямые
3х+4у–12=0 и х–4у–4=0
| х | х | |||||
| у | у | –1 |

Координаты точки О(0;0) удовлетворяют и неравенству 3х+4у-12<0 и неравенству х-4у-4<0. Искомая область – угол, образованный построенными прямыми (двойная штриховка).
2) 
Прямая у–4=0 параллельна оси Ох, а неравенство у>4 определяет полуплоскость, лежащую «выше» прямой. Прямая х–у=0 или у=х совпадает с биссектрисой первого и третьего координатных углов. Нужная полуплоскость лежит «ниже» биссектрисы, т. к. у<х.

Искомая область – угол под двойной штриховкой.
3) 
2х-3у+6=0 4х-6у-9=0
| х | -3 | х | 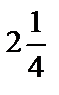
| |||
 у у
| у | 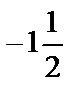
|
Искомая область – полоса между двумя параллельными прямыми.
4) 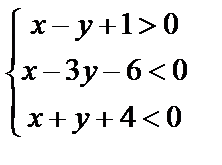
х–у+1=0, х–3у-6+0, х+у+4=0
| х | -1 | х | х | -4 | ||||||
| у | у | -2 | у | -4 |

Искомая область – треугольник (под тройной штриховкой).
Дата добавления: 2014-12-30; просмотров: 3034;
