Обзор кривых второго порядка
Прямая на плоскости является линией первого порядка, так как определяется уравнением первой степени с двумя переменными. Рассмотрим кривые второго порядка, то есть линии, определяемые в декартовых координатах уравнениями второй степени. Установлено, что таких линий всего четыре: окружность, эллипс, гипербола и парабола.
В п. 4 было получено уравнение окружности с центром С(х0, у0) и радиусом r:
(х–х0)2 + (у–у0)2 = r2 (14)
Из этого уравнения можно получить так называемое общее уравнение окружности: x2+y2+m×x+n×y+p=0. Заметим, что коэффициенты при х2 и у2 в уравнении окружности одинаковы. Если же в уравнении коэффициенты при х2 и у2 будут разными по величине, но одного знака, то такое уравнение будет определять эллипс.
Простейшее (каноническое) уравнение эллипса имеет вид:
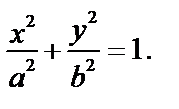 (15)
(15)
Чтобы построить такой эллипс, отметим точки пересечения эллипса с осями координат: А1(a, 0), А2(-а, 0), В1(0, b), В2(0, -b), называемые вершинами эллипса. Расстояние между вершинами |А1А2|=2а и |В1В2|=2b называют осями, а числа а и b – полуосями эллипса (а>0, b>0). Из уравнения (15) эллипса видно, что эллипс – фигура, симметричная относительно обеих осей и начала координат. Для точного построения эллипса используем определение:
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная.
Фокусы F1(c, 0) и F2(–c, 0) построим, учитывая,
что 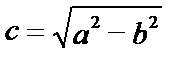 (при а>b).
(при а>b).
По определению сумма 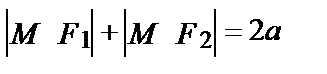 остается постоянной для любой точки М(х, у) эллипса.
остается постоянной для любой точки М(х, у) эллипса.

Если центр симметрии эллипса расположен в точке С(х0, у0) и оси симметрии параллельны координатным осям, то уравнение эллипса:
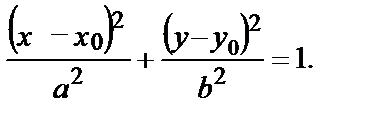 (16)
(16)

В школьном курсе гипербола рассматривается как график обратной пропорциональной зависимости 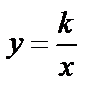 .
.
Рассмотрим более общий случай гиперболы, начав с ее определения:
Гиперболой называется множество точек плоскости, разность расстояний каждой из которых от двух данных точек есть величина постоянная. Простейшее (каноническое) уравнение гиперболы имеет вид:
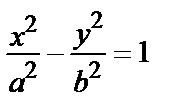 (17)
(17)
Как видно, коэффициенты при х2 и у2 имеют разные знаки.
Числа а и b (а>0 и b>0) называются полуосями гиперболы.
Точки А1(а,0), А2(–а,0), В1(0,b) и В2(0,–b) называют вершинами гиперболы.
Построим прямоугольник со сторонами, проходящими через вершины А1, А2, В1, В2 параллельно координатным осям. Диагонали этого прямоугольника называют асимптотами гиперболы. Очевидно, уравнения асимптот
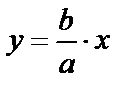 и
и 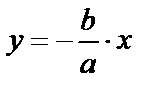
Через вершины А1(а, 0) и А2(-а, 0) проведем теперь две симметричные относительно координатных осей ветви гиперболы так, чтобы по мере удаления от центра симметрии – точки О(0,0) – они приближались бы к асимптотам, но не пересекали бы их.

Если же центр симметрии гиперболы расположен в точке С(х0, у0) и оси симметрии параллельны координатным осям, то уравнение гиперболы имеет вид:
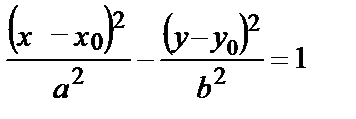 ,
,
Укажем, что гипербола является и графиком дробно-линейной функции 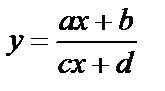 .
.
Параболу в школьном курсе рассматривают как график квадратного трехчлена у=ах2+bх+с.
Выделяя из квадратного трехчлена полный квадрат, это уравнение легко привести к виду
(х–х0)2=±2р×(у–у0) (18)

Здесь точка С(х0, у0) – вершина параболы, ось симметрии параллельна Оу. Коэффициент р(р>0) называют параметром параболы. Знак плюс перед коэффициентом 2р соответствует параболе, ветви которой направлены вверх, знак минус – вниз.
Можно рассмотреть параболу с осью симметрией, параллельной оси Ох. Ее уравнение имеет вид
(у–у0)2 = ±2р × (х–х0). (19)

Отметим, что уравнение параболы содержит квадрат только одной переменной: либо х (формула 18), либо у (формула 19).
Дадим определение, которое часто фигурирует как определение параболы.
Параболой называется множество точек плоскости, равноудаленных от данной прямой и от данной точки.
В заключение данного обзора кривых второго порядка отметим, что эти линии часто встречаются в различных вопросах естествознания. Например, движение материальной точки под воздействием центрального поля силы тяжести происходит по одной из этих линий.
Оптические свойства эллипса, гиперболы и параболы широко используется в инженерном деле. В частности, оптические свойства параболы используется при конструировании прожекторов, антенн, телескопов.
Такие термины, как «эллиптическая орбита», «эллипсоид инерции», «параболическая траектория», «параболическое зеркало» и т. д., убеждают в широком применении кривых второго порядка.
Вопросы для самоконтроля
Прежде чем Вы приступите к выполнению контрольного задания, попробуйте ответить на предлагаемые вопросы для самоконтроля. Если Вы будете испытывать затруднения при ответе на конкретный вопрос, попытайтесь найти на него ответ, вернувшись к теоретической части курса. Было бы лучше, если бы Вы воспользовались любым стандартным учебником по аналитической геометрии.
1. Что можно сказать о взаимном расположении векторов:
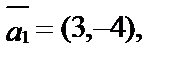
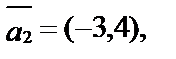
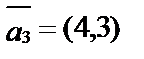 ,
, 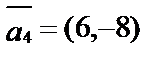 ?
?
2. Как расположены векторы в декартовой системе координат на плоскости: 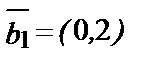 ;
; 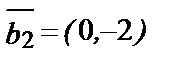 ;
; 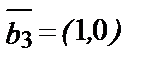 ;
;  ?
?
3. Среди векторов укажите равные векторы, коллинеарные векторы, векторы одинаковой длины, взаимно перпендикулярные векторы:
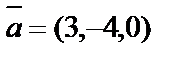 ,
, 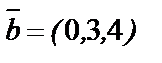 ,
,  ,
, 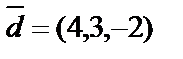 .
.
4. Как найти точку пересечения двух линий на плоскости, если уравнения этих линий даны?
5. Каков геометрический смысл системы 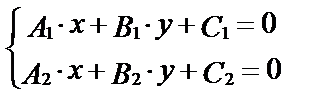 и ее решения?
и ее решения?
6. Какое множество точек на плоскости определяется уравнением
1) х=2; 2) х+3=0; 3) у=–1;
4) у–3=0; 5) х+у=0; 6) у=|х| ?
7. Какое множество точек на плоскости определяется системой неравенств:
1) 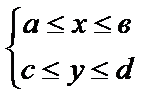 2)
2)  ?
?
8. Какое множество точек в пространстве определяется уравнением:
1) х+у=1, 2) х=5 3) z=-2?
9. Какое множество точек в пространстве определяется системой неравенств:
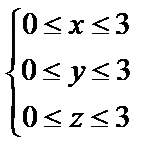 ?
?
2.10. Как выполнить контрольное задание № 2 «Элементы векторной алгебры и аналитической геометрии»
Задача № 1
Дан треугольник АВС:
А(4, 2), В(-2, 1), С(2, -3).
Найти длины и уравнения его сторон, угол при вершине B, площадь треугольника, уравнение описанной окружности. Записать систему неравенств, определяющих область треугольника.
При решении этой задачи будут использованы формулы, полученные в п. 4.
1) Найдем длины сторон по формуле 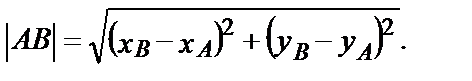
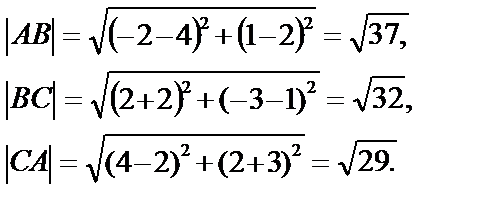
2) Составим уравнение каждой стороны треугольника по формуле (4):
Уравнение АВ: 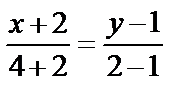 или у–1=
или у–1= 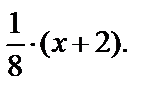
Уравнение ВС: 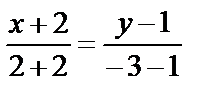 или у–1= –(х + 2).
или у–1= –(х + 2).
Уравнение АС: 
 или
или 
3) Для вычисления угла при вершине В найдем координаты векторов 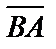 и
и 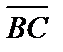 , выходящих из точки В и совпадающих со сторонами треугольника:
, выходящих из точки В и совпадающих со сторонами треугольника:
 ;
; 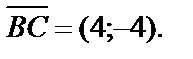
Тогда величина искомого угла  найдется из формулы:
найдется из формулы:
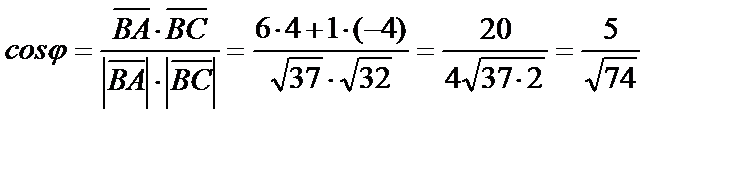
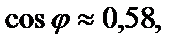
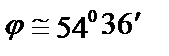 .
.
4) Вычислим площадь треугольника по формуле (11):
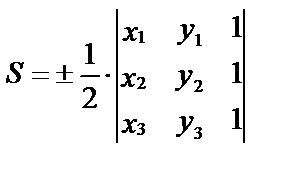
Подставив координаты вершин А, В, С, получим:

S=14(кв. ед.).
Здесь определитель равен положительному числу 28, поэтому следует взять знак плюс.
5) Центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров к сторонам треугольника.
Найдем координаты середин двух сторон АВ и ВС и проведем через эти точки прямые, перпендикулярные сторонам треугольника.
Итак, пусть точка D – середина АВ.
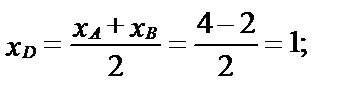
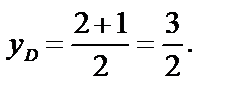
Через точку D (1; 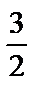 ) проведем прямую с угловым коэффициентом k2, который найдем из условия перпендикулярности прямых: k2= –
) проведем прямую с угловым коэффициентом k2, который найдем из условия перпендикулярности прямых: k2= – 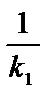 , где
, где 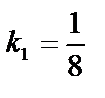
 (см. уравнение АВ). k2= – 8.
(см. уравнение АВ). k2= – 8.
Уравнение перпендикуляра: у– 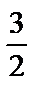 = –8×(х–1) или 16х + 2у–19 = 0. Точка Е – середина ВС и ее координаты:
= –8×(х–1) или 16х + 2у–19 = 0. Точка Е – середина ВС и ее координаты: 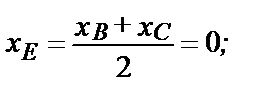

Через точку Е (0, –1) проведем прямую с угловым коэффициентом k=1, т. к. уравнение ВС: у–1=–(х+2).
Уравнение этого перпендикуляра: у+1=х или х–у–1=0.
Центр окружности (точку Р) найдем как точку пересечения найденных перпендикуляров из системы:
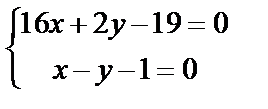 .
.
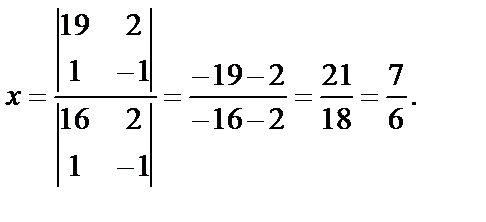
Тогда у = х – 1 = 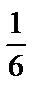 .
.
Точка Р ( 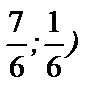 – центр описанной окружности, радиус которой r =
– центр описанной окружности, радиус которой r = 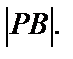 Найдем
Найдем  .
.
Уравнение описанной окружности –
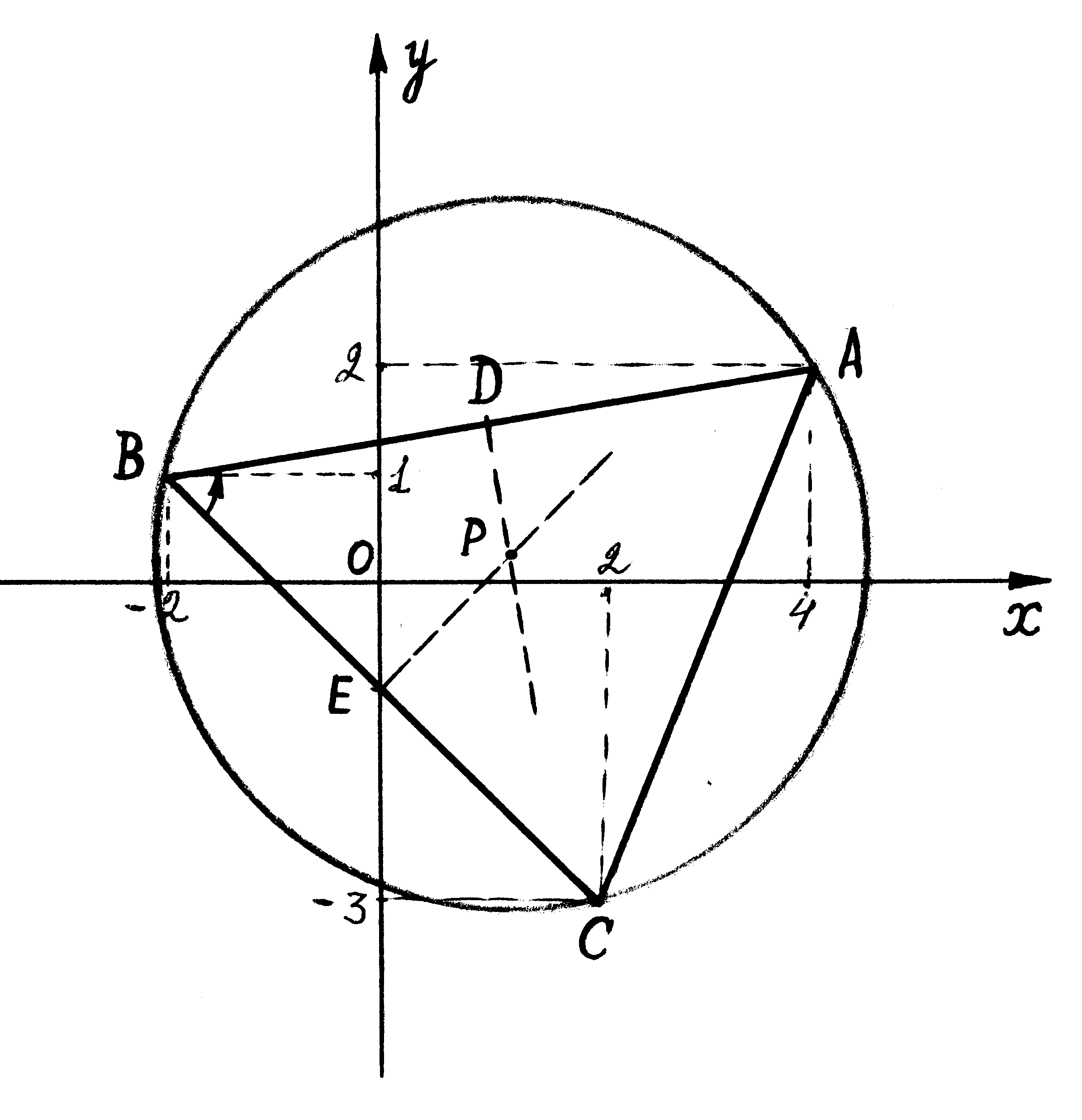
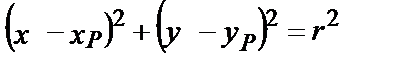 или
или 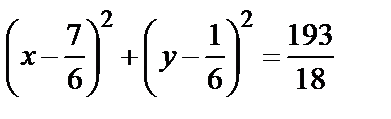 .
.
Составим систему неравенств, определяющих область треугольника АВС.
Уравнение прямой АВ: 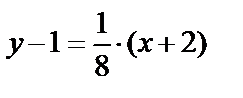 или х – 8у + 10 = 0.
или х – 8у + 10 = 0.
Найдем ту полуплоскость с границей на прямой х – 8у + 10 = 0, в которой лежит вершина С(2, –3). Подставив ее координаты в левую часть уравнения прямой АВ, получим неравенство 2 – 8×(–3) + 10 < 0. Поэтому нужная нам полуплоскость определяется неравенством х – 8у + 10 < 0.
Уравнение прямой ВС: у – 1 = –(х + 2) или х + у + 1 = 0. Координаты точки А (4, 2) дают неравенство 4 + 2 + 1 > 0. Поэтому область треугольника лежит в полуплоскости, для которой х + у + 1 > 0.
Уравнение прямой АС: у + 3= 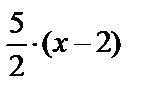 или 5х – 2у – 16 = 0.
или 5х – 2у – 16 = 0.
Координаты точки В (–2, 1) позволяют выбрать нужную полуплоскость:
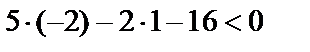 , т.е. 5х – 2у – 16 < 0.
, т.е. 5х – 2у – 16 < 0.
Система неравенств  определяет область треугольника АВС.
определяет область треугольника АВС.
Задача № 2.
Даны точки М1(–1,2,0), М2(1,–2,1), М3(3,1,–1), М4(3,0,1).
Составить уравнение плоскости, проходящей через
1) точки М1, М2, М3;
2) точку М4 параллельно плоскости М1 М2 М3;
3) точку М4 перпендикулярно вектору 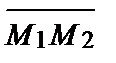 .
.
Вычислить объем пирамиды М1М2М3М4.
При решении этой задачи используются формулы из п. 6 и п. 7.
1) Составим уравнение плоскости, проходящей через три точки М1, М2, М3 по формуле (13):
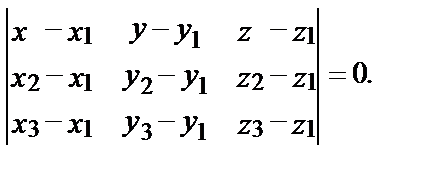
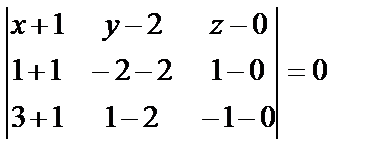 или 5х + 6у + 14z – 7 = 0.
или 5х + 6у + 14z – 7 = 0.
Подставив координаты точек М1, М2, М3 в полученное уравнение, убедимся, что уравнение составлено верно.
2) Коэффициенты при х, у, z в полученном уравнении (А=5; В=6; С=14) определяют положение параллельной плоскости, проходящей через точку (х0, у0, z0) по формуле (7):
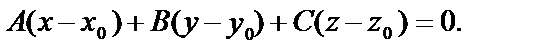
Уравнение плоскости, проходящей через точку М4(3,0,1) параллельно плоскости М1М2М3 имеет вид:
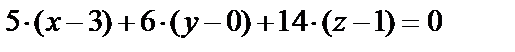 или 5х + 6у + 14z – 29 = 0.
или 5х + 6у + 14z – 29 = 0.
3) Принимая вектор 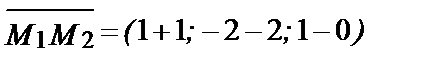 за нормальный вектор плоскости, составим уравнение плоскости, проходящей через точку М4 (3,0,1) перпендикулярно вектору
за нормальный вектор плоскости, составим уравнение плоскости, проходящей через точку М4 (3,0,1) перпендикулярно вектору 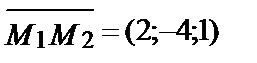 :
:
2×(х–3)–4(у–0) + 1×(z–1) = 0 или 2х–4у + z– 7 = 0.
4) Объем пирамиды М1М2М3М4 вычислим, используя формулу (12):
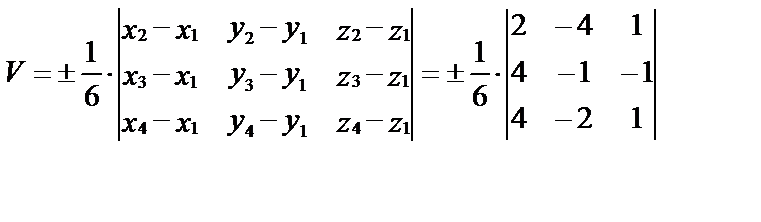 .
.
V= 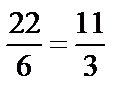 (куб. ед.).
(куб. ед.).
Задача № 3.
Какую линию определяет уравнение?
а) Дано уравнение:
16х2 + 25у2 – 96х + 50у – 231 = 0.
Приведем его к простейшему виду, выделив полные квадраты с переменной х и с переменной у:
16×(х2 – 6х + 9) – 16×9 + 25×(у2 + 2у + 1) – 25 – 231 = 0.
16×(х – 3)2 + 25×(у + 1)2 = 400.
Разделим обе части на 400:
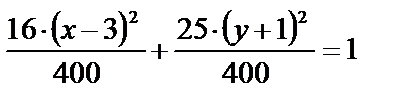 или
или 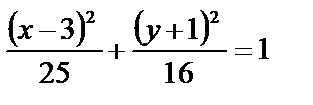 .
.
Получено уравнение эллипса (16) с полуосями а=5, b=4 и центром симметрии в точке С(3,–1).
Построим эллипс, оси симметрии которого проходят через точку С(3,–1) параллельно координатным осям. Их уравнения х = 3 и у = –1.
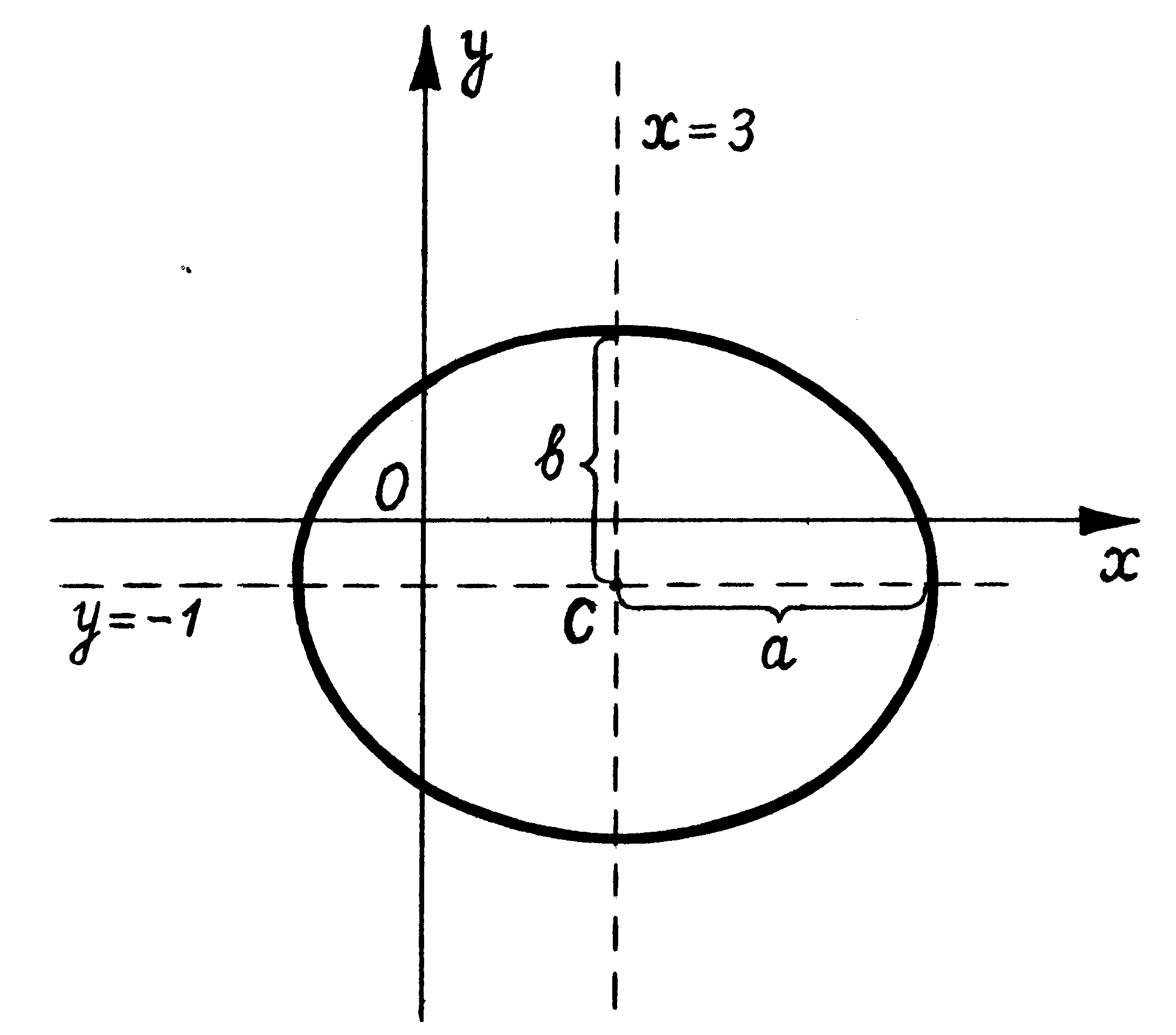
б) Дано уравнение:
9х2 + 4у2 + 18х – 16у – 11 = 0.
Преобразуем его:
9(х2 + 2х + 1) – 9 + 4(у2 – 4у + 4) – 16 – 11 = 0
9(х + 1)2 + 4(у – 2)2 = 36
 .
.
Это уравнение эллипса с центром симметрии в точке С(–1,2). Оси симметрии имеют уравнения: х = –1 и у = 2.
Полуоси эллипса а = 2 и b = 3, т. е. эллипс вытянут по оси Оу.
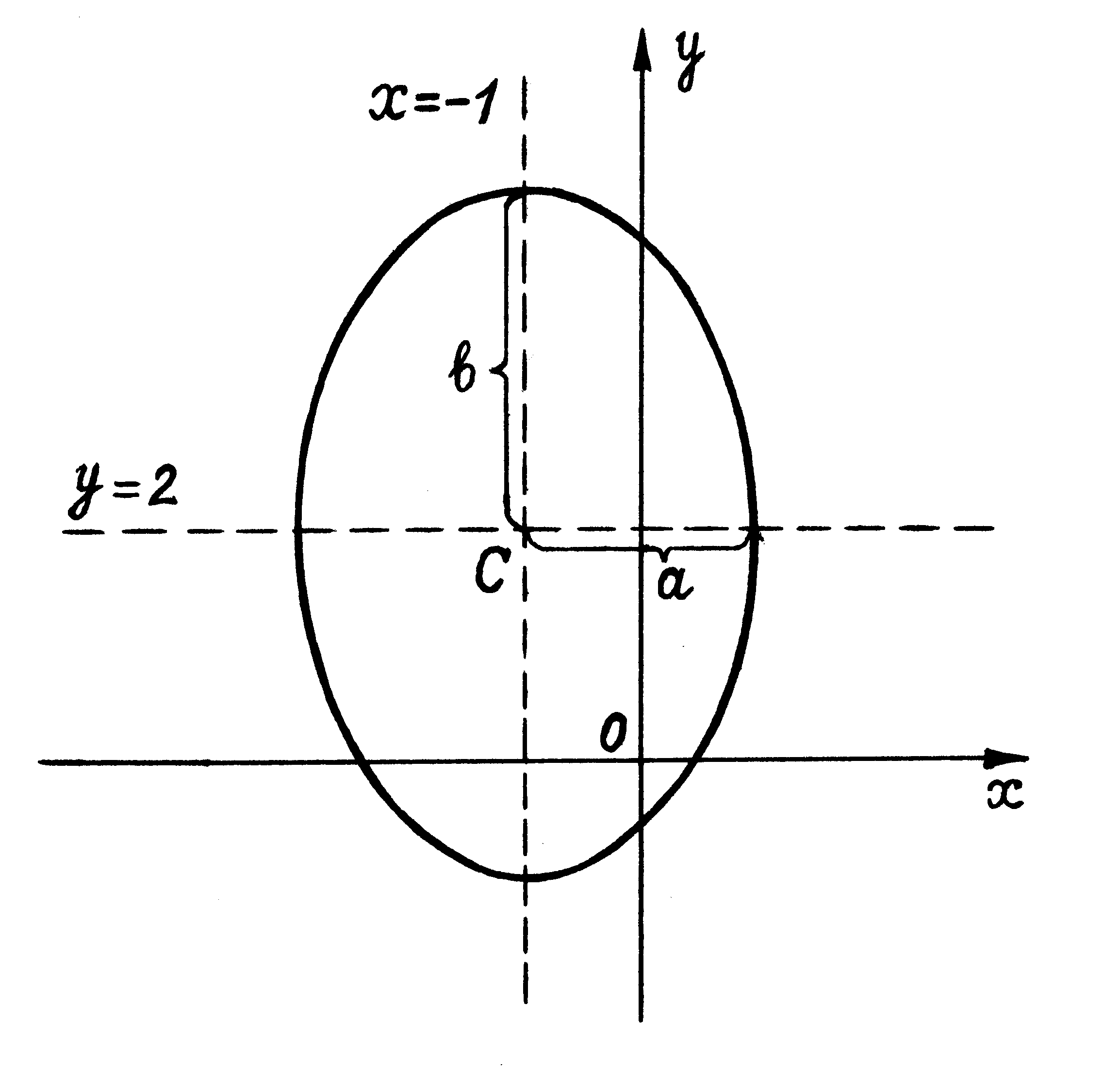
Дата добавления: 2014-12-30; просмотров: 2286;
