Аналитическая геометрия на плоскости. 1. Расстояние d между точками и определяется по формуле:
1. Расстояние d между точками 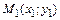 и
и 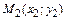 определяется по формуле:
определяется по формуле:
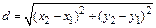 . (1)
. (1)
Уравнение прямой, проходящей через точки 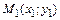 и
и 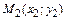 , имеет вид:
, имеет вид: 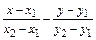 . (2)
. (2)
Угол 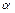 между двумя прямыми, угловые коэффициенты, которых равны
между двумя прямыми, угловые коэффициенты, которых равны 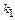 и
и 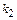 , определяется по формуле:
, определяется по формуле:
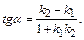 (3)
(3)
Если прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку, т.е.
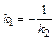 .
.
Уравнение прямой, проходящей через данную точку 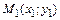 в заданном угловым коэффициентом k направлении, имеет вид:
в заданном угловым коэффициентом k направлении, имеет вид:

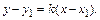 (4)
(4)
2. Кривые второго порядка.
В прямоугольной декартовой системе координат x0y кривая второго порядка задается уравнением второй степени
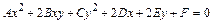 , (5)
, (5)
где A, B, C, D, E, F- заданные действительные числа. При этом числа A, B, C одновременно не равны нулю. Уравнение (5) называется общим уравнением кривой второго порядка.
Эллипс
Эллипсомназывается множество точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть величина постоянная.
Если известны расстояние между фокусами 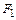 и
и 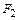 эллипса, равное 2с, и сумма расстояний от любой точки на эллипсе до фокусов, равная 2а, то в прямоугольной декартовой системе координат, где ось 0x проходит через фокусы
эллипса, равное 2с, и сумма расстояний от любой точки на эллипсе до фокусов, равная 2а, то в прямоугольной декартовой системе координат, где ось 0x проходит через фокусы 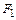 и
и 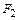 (от
(от 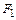 к
к 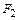 ), а начало координат находится посередине между ними, уравнение эллипса имеет вид:
), а начало координат находится посередине между ними, уравнение эллипса имеет вид:
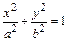 ,
,
который называется каноническим, числа а и b 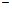 полуосями эллипса; а, b>
полуосями эллипса; а, b> 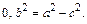 Вид кривой показан на рис.2.
Вид кривой показан на рис.2.
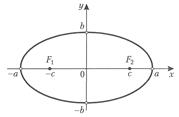
Рис. 2
При а=b эллипс представляет собой окружность радиусом а с центром в начале координат. Уравнение этой окружности
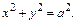
Эксцентриситетом эллипса называется число 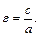 Для эксцентриситета эллипса справедливо неравенство
Для эксцентриситета эллипса справедливо неравенство 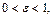 поскольку из определения эллипса следует, что
поскольку из определения эллипса следует, что 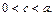 Эксцентриситет окружности
Эксцентриситет окружности 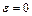 , поскольку для окружности а=b и с=0.
, поскольку для окружности а=b и с=0.
Дата добавления: 2014-12-03; просмотров: 1956;
