Аналитическая геометрия в пространстве.

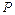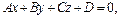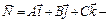1. Общее уравнение плоскости имеет вид где нормальной вектор плоскости (рис. 6).

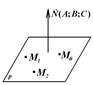
Рис.6

Уравнение плоскости, проходящей через три заданные точк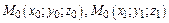и и 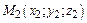имеет вид:

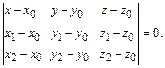(6)

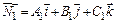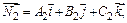2. Угол между двумя плоскостями, имеющими нормальные векторы и определяется как угол между 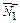и 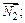косинус этого угла находится по формуле

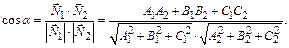(7)

3. Расстояние от точки 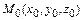до плоскости, определяемой уравнением 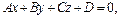находится по формуле

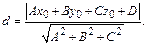(8)

4. Уравнение плоскости, проходящей через точку 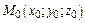и перпендикулярной вектору 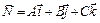, имеет вид

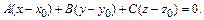(9)

5. Уравнения прямой в пространстве, проходящей через две заданные точк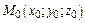и и 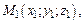имеют вид:

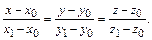(10)