Термодинамические потенциалы

Физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно полученному или отданному количеству теплоты, деленному на температуру,при которой произошел этот переход, называется энтропией.

Для бесконечно малого изменения состояния системы:

dS=dQ/T.

При переходе системы из одного состояния вдругое, изменение энтропии можно рассчитать так:

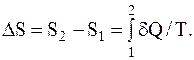
На основании первого начала термодинамики можно получить

dS=dQ/T=C_VdT/T+RdV/V, а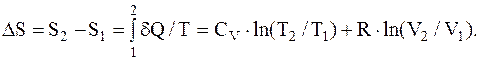

При изотермическом процессе T=const, т.е. T₁=T₂:

DS=R×ln(V₂/V₁).

При изобарическом процессе p=const, т.е. V₂/V₁=T₂/T₁:

DS=(C_V+R)×ln(T₂/T₁)=C_p×ln(T₂/T₁)=C_p×ln(V₂/V₁).

При изохорическом процессе V=const, т.е. V₁=V₂:

DS=C_V×ln(T₂/T₁).

При адиабатическом процессе dQ=0, т.е. DS=0:

S₁=S₂=const.

Изменения энтропии системы, совершающей цикл Карно:

DS=-(Q₁/T₁+Q₂/T₂).

Энтропия замкнутой системы, совершающей обратимый цикл Карно не изменяется:

dS=0 или S=const.

Если системой совершается необратимый цикл, то dS>0.

Таким образом, энтропия замкнутой (изолированной) системы при любых, происходящих в ней процессах не может убывать:

dS³dQ/T,

где знак равенства справедлив для обратимых процессов, а знак неравенства – для необратимых.

Второе начало термодинамики: "В изолированной системе возможны только такие процессы, при которых энтропия системы возрастает". То есть

dS³0 или dS³dQ/T.

Второе начало термодинамики определяет направление термодинамических процессов и указывает на физический смысл энтропии: энтропия – мера рассеяния энергии, т.е. характеризует ту часть энергии, которую нельзя превратить в работу.

Термодинамическими потенциалами называют определенные функции объема V, давления p, температуры T, энтропии S, числа частиц системы N и других макроскопических параметров x, характеризующих состояние термодинамической системы. К ним относятся: внутренняя энергия U=U(S,V,N,x), энтальпия H=H(S,p,N,x); свободная энергия – F=F(V,T,N,x), энергия Гиббса G=G(p,T,N,x).

Изменение внутренней энергии системы в каком-нибудь процессе определяют как алгебраическую сумму количества теплоты Q, которыми система обменивается в ходе процесса с окружающей средой, и работы А, совершенной системой или произведенной над ней. Это отражает первое начало термодинамики:

DU=Q+A.

Изменение U определяется лишь значениями внутренней энергии в начальном и конечном состояниях:

DU=U₂-U₁.

Для любого замкнутого процесса, возвращающего систему в первоначальное состояние, изменение внутренней энергии равно нулю (U₁=U₂; DU=0; Q=A).

Изменение внутренней энергии системы в адиабатическом процессе (при Q=0) равно работе, производимой над системой или произведенной системой DU=A.

В случае простейшей физической системы с малым межмолекулярным взаимодействием (идеального газа) изменение внутренней энергии сводится к изменению кинетической энергии молекул:

DU=mc_VT,

где m – масса газа;

c_V – удельная теплоемкость при постоянном объеме.

Энтальпия (теплосодержание, тепловая функция Гиббса) – характеризует состояние макроскопической системы в термодинамическом равновесии при выборе в качестве основных независимых переменных энтропии S и давления p – H(S,p,N,x).

Энтальпия аддитивная функция (т.е. энтальпия всей системы равна сумме энтальпий составляющих ее частей). С внутренней энергией U системы энтальпия связана соотношением:

H=U+pV,

где V – объем системы.

Полный дифференциал энтальпии (при неизменных N и x) имеет вид:

dH=TdS+Vdp.

Из этой формулы можно определить температуру T и объем V системы:

T=(dH/dS), V=(dH/dp).

При постоянном давлении теплоемкость системы

c_p=(dH/dT).

Эти свойства энтальпии при постоянном давлении аналогичны свойствам внутренней энергии при постоянном объеме:

T=(dU/dS), p=-(dU/dV), c_V=(dU/dT).

Свободная энергия – одно из названий изохорно-изотермического термодинамического потенциала или Гельмгольца энергии. Она определяетсякак разность между внутренней энергии термодинамической системы (U) и произведением ее энтропии (S) на температуру (T):

F=U-TS,

где TS – связанная энергия.

Энергия Гиббса – изобарно-изотермический потенциал, свободная энтальпия, характеристическая функция термодинамической системы при независимых параметрах p, T и N – G. Определяется через энтальпию H, энтропию S и температуру T равенством

G=H-TS.

Со свободной энергией – энергией Гельмгольца, энергия Гиббса связана соотношением:

G=F+pV.

Энергия Гиббса пропорциональна числу частиц N, отнесенная к одной частице, называется химическим потенциалом.

Совершаемая термодинамической системой в каком-либо процессе работа определяется убылью термодинамического потенциала, отвечающего условиям процесса. Так, при постоянстве числа частиц (N=const) в условиях теплоизоляции (адиабатический процесс, S=const) элементарная работа dA равна убыли внутренней энергии:

dA=-dU.

При изотермическом процессе (T=const)

dA=-dF

В этомпроцессе работа совершается не только за счет внутренней энергии, но и за счет поступающей в систему теплоты.

Для систем, в которых возможен обмен веществом сокружающей средой (изменение N), возможныпроцессы при постоянных p и T. В этом случае элементарная работа dA всех термодинамических сил, кроме сил давления, равна убыли термодинамического потенциала Гиббса (G), т.е.

dA=-dG.

Согласно теореме Нернста изменение энтропии (DS) при любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при температурах, приближающихся к абсолютному нулю, стремится к нулю

limS=0. T®0.

Другая эквивалентная формулировка теоремы Нернста: "При помощи последовательности термодинамических процессов нельзя достигнуть температуры, равной абсолютному нулю".