Строение и свойства жидкостей

Между среднем временем, в течение которого молекула жидкости совершает колебательное движение относительно данного положения равновесия, временем " оседлой " жизни – t₀, которое зависит от природы жидкости, и временем одного колебания относительно данного положения равновесия t, существует связь

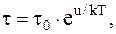
где U – "потенциальный барьер", численно равный разности энергий молекулы в двух возможных областях колебаний ("потенциальный барьер"

Т – температура жидкости;

k – постоянная Больцмана.

Вероятностная связь описывается функцией распределения F(r₁,r₂). В случае простой жидкости функция распределения зависит только от расстояния r=r₂-r₁ между молекулами и называется радиальной функцией распределения F(r).

Оценивается вязкость жидкостей по коэффициенту вязкости, который определяет величину силы трения между соседними ее слоями

F=-hS×(dv/dz),

где dv/dz – градиент скорости в направлении z;

S – поверхность соприкасающихся слоев жидкости.

В отличие от коэффициента вязкости в газах, который уменьшается с уменьшением температуры T, коэффициент вязкости жидкостей возрастает с уменьшением их температуры

l=h₀е^-u/kT,

где U – энергия необходимая для перехода молекулы жидкости из одного равновесного состояния в другое.

Текучесть жидкостей – свойство обратное вязкости, которое обусловлено той свободой движения молекул в объеме, которая еще допускается силами сцепления между ними.

Сжимаемость. Так как молекулы вжидкостях находятся значительно ближе друг к другу, чем в газах, то силы их межмолекулярного взаимодействия, вандерваальсовы силы, играют значительную роль, а, следовательно, внутреннее давление в жидкостях очень велико

p'=a/V².

Пренебрегая внешним давлением p в уравнении Ван дер Ваальса, уравнение состояния жидкости можно записать так:

am/(mV²)×(V-(m/m)b)=RT.

Коэффициент сжимаемости жидкостей K определяется соотношением

K=-1/V×(dV/dr),

где dV – уменьшение первоначального объема жидкости V при увеличении давления на dP.

Экспериментально было установлено, что с повышением температуры объем жидкости увеличивается согласно уравнению

V_t=V₀(1+at),

где a – коэффициент объемного расширения

a=1/V×(dV/dT).

Коэффициенты сжимаемости и объемного расширения жидкостей связаны между собой соотношением

a/K=-(dp/dT)_V.

Сила поверхностного натяжения

F=sℓ, a s=F/ℓ.

Следовательно, коэффициент поверхностного натяжения, численно равен силе поверхностного натяжения, которая стремится изменить длину (величину) контура, охватывающего поверхность жидкости, на единицу.

Зависимость коэффициента поверхностного натяжения от температуры:

dб/dT=-dQ/(TDS)=-r/T.

где r=dQ/DS – количество тепла, затраченное на изменение поверхности пленки на единицу.

Дополнительное молекулярное давление

Dp=F/S=2s/R.

Этот результат можно обобщить нажидкости, имеющие произвольную поверхность

Dp=s(1/R₁+1/R₂).

Данное соотношение называют формулой Лапласа.

Условие равновесиякапли на поверхности жидкости можно записать так

s₁₂+s₁₃×cosq=s₂₃.

где q – так называемый краевой угол.

Высота подъема (опускания) жидкости в капиллярах зависит от его радиуса:

h=2s×cosq/(rgr),

где r – радиус капилляра.

При q=0 – жидкость полностью смачивает стенки капилляра

h=2s/gr;

при q>p/2 – жидкость не смачивает стенки капилляра h<0, т. е. уровень жидкости в капилляре ниже уровня этой жидкости в сосуде.

В узком зазоре между погруженнымив жидкость параллельными пластинами также происходит поднятие или опускание жидкости. При этом мениск имеет цилиндрическую форму. Его радиус кривизны связан с расстоянием между пластинами соотношением

R=d/2 cosq.

В этом случае дополнительное давление

Dp=s/R.

Высота подъема жидкости

h=2s×cosq/(rgd).

За счет искривления поверхности жидкости, давление между пластинами меньше атмосферного на величину

Dp=s/R=2s/d.

Во всех точках жидкости, лежащих на одном уровне, давление имеет одинаковую величину:

p₁=p₂.

Давление на двух разных уровнях отличаются на величину, равную весу вертикального столба жидкости, заключенного между этими уровнями, с площадью сечения, равного единице:

p₂=p₁+rgh.

Для несжимаемой жидкости в стационарном потоке величина

Sv=const.

Это уравнение является математической формой записи теоремы о непрерывности струи. То есть

S₁v₁=S₂v₂.

В стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие

rv²/2+rgh+p=const.

Данное выражение называют уравнением Бернулли.

Оно устанавливает закон изменения давленияс изменением высоты h и скоростипотока v.

Если v₁=v₂ для двух сечений, то

p₂-p₁=rg(h₁-h₂),

то есть разность давлений оказывается такой же как и в покоящейся жидкости.

Для горизонтального потока h₁=h₂, изменение давления в потоке возникает только за счет изменения скорости потока. Давление оказывается меньше там, где скорость больше:

p+rv²/2=const,

где p – давление не зависящееот скорости – статическое давление жидкости;

rv²/2 – давление зависящее от скорости – динамическое давление, которое показывает на какую величину изменяется статическое давление при остановке движущегося потока жидкости.

Сумма статического и динамического давлений называют полным давлением потока.

Скорость частиц жидкостипо сечению трубы увеличиваетсяот нуля, у стенок трубы, до v=(p₁–p₂)R²/4hℓ у ее оси.

Через сечение трубы протекает объем жидкости

V=(p₁–p₂)pR⁴/8hℓ.

Эта формула была полученаПуазейлем. По ней можно вычислять коэффициент вязкости жидкости, зная скорость ее истечения.

Характер течения жидкости определяется числом Рейнольдса

R_е=rvℓ/h,

где r – плотность жидкости (газа);

v – средняя по сечению скорость движения жидкости;

ℓ – характерный для поперечного сечения размер (сторона квадрата, радиус круглого сечения ит.д.);

h – коэффициент вязкости.

При малом числе Рейнольдса течение жидкости ламинарное. Начиная с некоторого его значения, называемого критическим, течение жидкости приобретает турбулентный характер.

Величину n=h/r называют кинематической вязкостью. Величина h называется динамической вязкостью.