Примеры решения задач. 5.1. К пружинным весам подвешена тонкая металлическая пластина

5.1. К пружинным весам подвешена тонкая металлическая пластина. Нижний ее край длиной L=10,0 см приведен в соприкосновение с поверхностью жидкости, которая полностью смачивает пластину. После этого пластину начинают медленно поднимать. Перед ее отрывом от жидкости поверхность последней принимает сложную форму. При этом свободная поверхность жидкости у границы с пластиной располагается приблизительно в вертикальной плоскости. Зная, что для отрыва пластины потребовалась сила F=0,45×10^-3 кГс, определить коэффициент поверхностного натяжения жидкости.

Решение. Чтобы найти коэффициент поверхностного натяжения, нужно, как это следует из формулы б=F/ℓ, знать силу поверхностного натяжения, действующую на единицу длины какого-либо контура, ограничивающего поверхность жидкости. Таким контуром является линия соприкосновения свободной поверхности жидкости с пластиной, имеющей форму очень узкого прямоугольника. Следовательно, ее длина равна 2L (длиной двух других сторон пренебрегаем).

На пластину вдоль каждой единицы длины этого контура действует со стороны жидкости сила поверхностного натяжения, равная коэффициенту. Векторы этих сил перпендикулярны контуру и являются касательными к свободной поверхности жидкости. Поэтому в условиях данной задачи они направлены вертикально вниз и, следовательно, параллельны друг другу. Поэтому результирующая сила поверхностного натяжения F_н, действующая на пластину, также направлена вертикально вниз и равна сумме сил, действующих на отдельные элементы контура, т.е.

F=2Ls.

Для отрыва пластины от жидкости необходимо приложить силу F, направленную вертикально вверх, которая бы уравновесила силу поверхностного натяжения. Следовательно,

F_н=F=2Ls.

Откуда

s=F/2L.

Выразим входящие в формулу величины в единицах СИ: L=0,100 м, F=4,4×10^-3 Н. Выполнив вычисление, найдем

s=22×10^-3 Н/м.

Существенно, что в данной задаче пластина была тонкой, так что площадью ее соприкосновения с жидкостью, площадью прямоугольника, можно было пренебречь. В противном случае необходимо учитывать отрицательное давление, создаваемое в жидкости около пластины вследствие кривизны ее поверхности. Тогда соотношение F_н=F оказывается неверным. Кроме того, для толстой пластины силы поверхностного натяжения, приложенные к отдельным элементам прямоугольного контура, уже не будут даже приблизительно параллельны друг другу и поэтому соотношение F_н=2Ls также перестанет выполняться.

Решение задачи в случае толстой пластины становится сложным.

5.2. Какую работу против сил поверхностного натяжения надо совершить, чтобы выдуть мыльный пузырь радиусом 0,05 м? чему равно избыточное давление внутри пузыря?

Решение. Мыльный пузырь представляет собой очень тонкую мыльную пленку мыльной воды приблизительно сферической формы. Эта пленка имеет две поверхности – наружную и внутреннюю. Пренебрегая толщиной пленки и считая, поэтому радиусы сфер одинаковыми, их общая площадь будет равна

S=8pR².

Поскольку до образования пузыря поверхность мыльной воды, из которой он выдут, была весьма мала, можно считать, что записанное соотношение выражает изменение (прирост) площади DS поверхности мыльной воды.

Увеличение поверхности жидкости на DS связано с приростом поверхностной энергии

DW=sDS.

Совершаемая при выдувании пузыря работа против сил поверхностного натяжения идет на увеличение поверхностной энергии

A=DW=8pR²s.

Для определения избыточного давления внутри пузыря учтем, что каждая из двух сферических поверхностей пузыря – наружная и внутренняя – производит вследствие своей кривизны давление на воздух внутри пузыря. Это давление, производимое каждой сферой, можно найти по формуле Лапласа, имея в виду, что радиусы кривизны всех нормальных сечений для сферы равны ее радиусу, следовательно, R₁=R₂=R. Таким образом, избыточное давление воздуха внутри пузыря

Dp=2p_пов=4s/R.

Взяв из таблицы значение для мыльной воды (s=40×10^-3 Н/м) и выполнив вычисление, получим

A=2,5×10^-3 Дж=2,5 мДж;

Dp=3,2 Па.

5.3. Вертикально расположенная капиллярная трубка длиной ℓ=200 мм с запаянным верхним концом приведена в соприкосновение своим нижним концом с поверхностью воды. На какую высоту поднимется вода в трубке, если ее радиус R₀=2,0×10 м? Атмосферное давление p=1,00×10⁵ Па. Считать, что вода полностью смачивает трубку.

Решение. Здесь нельзя применять формулу:

h=2s/(rrg),

где r – плотность жидкости;

g – ускорение силы тяжести;

s – коэффициент поверхностного натяжения.

Эта формула определяет высоту поднятия жидкости в капилляре при полном смачивании и справедлива лишь для открытой с обоих концов трубки.

Для решения задачи рассмотрим столбик воды, находящийся в равновесии в капилляре, после того как он уже поднялся под действием сил поверхностного натяжения. Согласно условию равновесия разность давлений у его концов равна гидростатическому давлению, производимому столбиком жидкости высотой h на его основание, т.е.

p₁–p₂=rgh,

где p₁ и p₂ – давления внизу и вверху столба соответственно.

Давление внизу столба равно давлению в воде у ее открытой поверхности, т.е. атмосферному давлению

p₀=p₁,

так как в противном случае жидкость у нижнего края трубки не была бы в равновесии.

Поскольку столб воды ограничен сверху изогнутой поверхностью, давление p₂ вверху отличается от давления p_в воздуха в трубке на величину p_пов, определяемую формулой

p₂=p_в+p_пов.

При расчете давления pпов учтем, что мениск в узком капилляре имеет форму полусферы и, следовательно, R₁=R₂=R. Поэтому

p_пов=2s/R,

где R=R₀.

Так как данный мениск вогнутый, то p_пов<0. Значит, следует считать R=-R₀. Тогда

p_пов=-2s/R₀.

Давление воздуха в трубке можно выразить через данные величины p₀, ℓ, а также высоту столба h при помощи закона Бойля-Мариотта. Воздушный столб высотой (ℓ-h) при давлении p_в имел при атмосферном давлении p_o высоту ℓ. Поскольку объем столба пропорционален его длине, то можно записать:

p_в(ℓ-h)=p₀ℓ; p_в=p₀ℓ/(ℓ-h).

Подставим в формулу разности давлений значения p₁ и p₂ с учетом p_пов, p_в, будем иметь

p₀-(p₀ℓ/(ℓ-h)-2s/R)=rgh.

Взяв из таблиц значения s и r для воды, выразим в единицах СИ величины, входящие в последнее соотношение: p₀=1,00×10⁵ Па, ℓ=0,2 m, R_o=2,0×10^-4 м, s=0,073 Н/м, r=1,00×10³ кг/м³. Подставив их и решив квадратное уравнение относительно h, получим

h₁=11 м; h₂=0,014 м.

Поскольку должно выполняться очевидное неравенство h<ℓ, то ответом на вопрос задачи является второе значение.

5.4. На полированную стеклянную пластинку капнули 0,010 г воды и наложили сверху вторую такую же пластинку. Вода растеклась между пластинками по площади круга радиуса R=3,0 см, не дойдя до ее краев. С какой силой надо растягивать обе пластинки, чтобы их разъединить? Считать, что вода полностью смачивает стекло.

Решение. Сначала выясним, почему возникает сила притяжения между пластинками. При наложении пластинок свободная поверхность воды вследствие полного смачивания образует вогнутый мениск в виде полуокружностей. Следовательно, давление в жидкости, заключенной между пластинками, меньше атмосферного на величину p_пов, определяемую по формуле

p_пов=s(1/R₁+1/R₂),

где R₁ и R₂ – радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости. При этом p_пов положительно, если поверхность жидкости выпуклая, и отрицательно, если – вогнутая.

Под избытком внешнего давления пластины сближаются, вода растекается между ними все более тонким слоем. Этот процесс прекратится, когда жидкость дойдет до краев пластин, после чего мениск распрямится, а поверхностное давление и сила притяжения между пластинами исчезнут, или когда дальнейшее сближение пластин станет невозможным из-за того, что они начнут соприкасаться друг с другом в некоторых точках вследствие неровностей их поверхности. Очевидно, что именно последний случай имеет место в задаче.

Сила притяжения между пластинками равна избыточному внешнему давлению p_пов, умноженному на площадь одной пластины, т.е.

F=p_пов×S=p_пов×sR²,

где R – радиус круга растекания жидкости.

Чтобы определить величину p_пов, рассмотрим два взаимно перпендикулярных нормальных сечения поверхности жидкости. Очевидно, радиус кривизны R₁ первого сечения равен половине расстояния между пластинками, радиус кривизны R₂ второго сечения равен радиусу круга растекания жидкости. Поскольку при этом выполняется неравенство R₁<<R₂, то в формуле для избыточного давления, можно пренебречь величиной 1/R₂, т.е. кривизной второго сечения, и рассматривать мениск приближения как вогнутую цилиндрическую поверхность. Таким образом, получим

p_пов=s/R₁=2s/d,

где d – расстояние между пластинками, которое можно определить, разделив объем воды на площадь ее растекания:

d=V/S=m/rpR²,

где m – масса воды;

r – ее плотность.

Наконец определим силу притяжения между пластинками:

F=2p²srR⁴/m.

Чтобы разъединить пластинки, их надо растягивать с силой, по крайней мере, равной силе их взаимного притяжения. Таким образом, полученная формула дает ответ на поставленный в задаче вопрос.

Взяв из таблиц значения s и r для воды, выразим входящие величины в единицах СИ: R=3,0×10^-2 м, r=0,073 Н/м, r=1,00×10³ кг/м³, m=1,0×10^-5 кг. Произведем вычисление, получим

F=1,2×10³ Н=0,12 кН.

5.5. Найти плотность масла в гидравлической системе пресса при давлении 500×10⁵ Па, если плотность его при 20 ^oС и давлении 1,013×10⁵ Па равна 910 кг/м³, а коэффициент сжатия равен 6×10^-10 м²/Н.

Решение. По определению, коэффициент сжатия

К=-dV/V×dp,

где dV – изменение объема;

V – первоначальный объем;

dp – изменение давления.

Разделяя переменные имеем

-dV/V=K dp.

Проинтегрируем это выражение в заданных пределах:

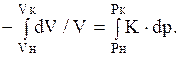
Получаем lnV_к/V_н=-K×Dp; или V_к=V_н exp(-КDp) ~ V_н(1-KDp).

Так плотность r=m/V, то m/V_к=m/V_н (1 – KDp), т.е.

r_к=r_н/(1-KDp).

Подставляя значения величин входящих в полученную формулу в единицах СИ, произведя вычисление, окончательно будем иметь

r_к=938 кг/м³.

5.6. В дне цилиндрического сосуда диаметром D=0,5 м имеется круглое отверстие диаметром d=1 см. Найти зависимость скорости понижения уровня воды в сосуде от высоты h этого уровня. Найти значение этой скорости для высоты h=0,2 м.

Решение. Обозначим: S₁ – площадь поперечного сечения сосуда и v₁ – скорость течения воды в нем (скорость понижения уровня воды в сосуде), S₂ – площадь поперечного сечения отверстия и v₂ – скорость вытекания воды из отверстия.

По теореме Бернулли

rv²₁/2+rgh=rv₂²/2, или v₁²+2gh=v₂²,

v₁²=v₂²-2gh,

где r – плотность воды;

g – ускорение силы тяжести;

h – высота уровня жидкости.

В силу теоремы о неразрывности струи

v₁S₁=v₂S₂.

Откуда

v₂=v₁S₁/S₂.

Подставляя v₂ в формулу v₁, будем иметь

v₁²=(v₁S₁/S₂)²-2gh.

Решая полученное уравнение относительно v₁, получим

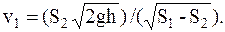
Учитывая, что S₁=pD²/4 и S₂=pd²/4, имеем

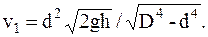
Так как d⁴<<D⁴, то приближенно, скорость понижения уровня воды в сосуде от высоты h этого уровня, определяется соотношением

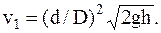
Отметим, что если d=D, то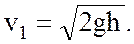

При h=0,2 м скорость v ₁=0,8 мм/с=0,8×10^-3 м/с.

5.7. В боковую поверхность цилиндрического сосуда радиусом R=2 см вставлен горизонтальный капилляр, внутренний радиус которого r=1 мм и длина ℓ=2 см. В сосуд налито касторовое масло, динамическая вязкость которого h=1,2 Па×с. Найти зависимость скорости v понижения уровня касторового масла в сосуде от высоты h этого уровня над капилляром. Найти значение этой скорости при h =26 см.

Решение. Скорость понижения уровня касторового масла в сосуде зависит от скорости протекания масла через капилляр.

Объем масла, протекающего за время t через капилляр, определяется формулой Пуазейля

V=pr⁴tDp/8ℓh,

где r – радиус капилляра;

Dp – изменение давления на концах капилляра;

ℓ – длина капилляра;

h – динамическая вязкость жидкости (касторового масла).

Разность давлений на концах капиллярах обусловлена гидростатическим давлением слоя жидкости, т.е.

Dp=rgh.

С другой стороны,

V=S'v't=pr²v't,

где v' – скорость протекания масла через капилляр.

Решая совместно вышенаписанные уравнения относительно v, получим

v'=r²rgh/(8ℓh).

В силу теоремы о неразрывности струи

v₁S₁=v₂S₂,

где v – скорость понижения уровня масла в сосуде;

S – площадь поперечного сечения сосуда.

Окончательно для скорости понижения уровня масла в сосуде, будем иметь

v=r⁴rgh/(8ℓhR²).

При h=0,26 м скорость v=3×10^-5 м/с.