С учетом этого будем иметь

DS=(m/m)Rln(V₂/V₁).

Подставив числовые значения в единицах системы СИ, и произведя вычисления, получим

S=3,6 Дж/К.

4.3. Струя водяного пара при температуре 100 ^oС, направленная на глыбу льда, имеющую массу m=5 кг и температуру 0 ^oС, растопила ее и нагрела получившуюся воду до температуры 50 ^oС. Найти массу израсходованного пара и изменение энтропии при описанных процессах.

Решение. Количество теплоты, необходимое для плавления льда и для нагревания полученной холодной воды, равно количеству теплоты, выделившейся при превращении пара в воду той же температуры и последующем охлаждении полученной горячей воды. Составим уравнение теплового баланса:

m₁l+cm₁(q-t₁)=m₂r+cm₂(t₂-q),

где m₁ – масса льда;

m₂ – масса пара;

l – удельная теплота плавления льда;

r – удельная теплота парообразования воды;

c – удельная теплоемкость воды;

q – температура смеси;

t₁ – температура плавления льда;

t₂ – температура кипения воды.

Решая уравнение относительно m₂, получаем

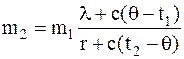
Подставим числовые значения величин в единицах СИ: l=3,35×10⁵ Дж/кг, r=2,25×10⁶ Дж/кг, c=4,19×10³ Дж/(кг×град), m₁=5 кг, произведем вычисление, будем иметь

m₂=1,11 кг.

Изменение энтропии DS равно сумме изменений энтропии при таянии льда (DS₁), при нагревании получившейся холодной воды (DS₂), при превращении пара в воду той же температуры (DS₃) и, наконец, при охлаждении полученной горячей воды до окончательной температуры смеси (DS₄).

Изменение энтропии при переходе системы из состояния 1 в состояние 2 выражается формулой

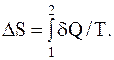
Найдем изменение энтропии при каждом из описанных процессов:

1) при таянии льда температура T сохраняет постоянное значение, равное 273 К. Вынося постоянную температуру за знак интеграла, получаем

DS=Q₁/T,

где Q₁=lm₁ – количество теплоты, необходимое для таяния льда;

Следовательно

DS₁=lm₁/T.

2) при нагревании воды на dT требуется количество теплоты, равное:

dQ₂=cm₁dT.

Следовательно, изменение энтропии при нагревании воды выразится так:

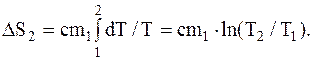
3) при превращении пара в воду той же температуры изменение энтропии может быть найдено на основании тех же соображений, что и в случае таяния льда, т.е.

DS₃=Q/T=-rm₂/T.

Изменению энтропии приписывается знак "минус", так как теплота выделяется.

4) наконец, изменение энтропии, происходящее при охлаждении полученной горячей воды, найдем на основании тех же рассуждений, что и в случае нагревания воды, т.е.

DS₄=-cm₂ln(T₂/T₁).

Знак "минус" – так как теплота отбирается.

Полное изменение энтропии рассмотренных процессов будет равно:

DS=DS₁+DS₂+DS₃+DS₄,

DS=lm₁/T₁+cm₁ln(q/T₁)-rm₂/T₂-cm₂×ln(q/T₂).

Подставляя численные значения величин в единицах СИ, произведем вычисление, имеем

DS=2,27×10³ Дж/град.

4.4. Исходя из второго начала термодинамики, вывести формулу для КПД цикла Карно.

Решение. Наиболее общим выражением второго начала термодинамики является формула

DS³0.

Поскольку цикл Карно представляет собой обратимый процесс, из этой формулы следует, что полное изменение энтропии изолированной системы нагреватель – рабочее вещество – холодильник равно нулю:

DS=0.

Согласно свойству аддитивности, полное изменение энтропии системы DS будет складываться из изменений энтропии нагревателя DS₁, рабочего вещества DS' и холодильника DS₂:

DS=DS₁+DS'+ DS₂.

Рассмотрим эти изменения энтропии за один цикл. Так как рабочее вещество, совершив цикл, вернется в первоначальное состояние, а энтропия является функцией состояния, то она примет также первоначальное значение, т.е. DS'=0. Следовательно, имеем

DS=DS₁+DS₂=0.

Изменение энтропии нагревателя DS₁ и холодильника DS₂ можно определить по формуле

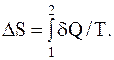
Нагреватель отдает рабочему веществу количество теплоты Q₁ при постоянной температуре T₁, переходя при этом из некоторого состояния 1 в состояние 2. Поэтому приращение dQ берем со знаком "минус":

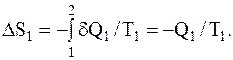
Холодильник получает от рабочего тела количество теплоты Q₂ при температуре T₂, переходя из некоторого состояния 3 в состояние 4. Следовательно,

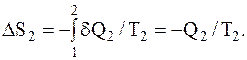
Подставим эти значения DS₁ и DS₂ в формулу для полного изменения энтропии, будем иметь

-Q₁/T₁+Q₂/T₂=0 или -Q₁/T₁=-Q₂/T₁.

Откуда

-Q₂/Q₁=-T₂/T₁.

Прибавив к обеим частям равенства по единице, найдем

h=(Q₁–Q₂)/Q₁=(T₁–T₂)/T₁.

4.5. Теплоизолированный сосуд разделен на две равные части перегородкой, в которой имеется закрывающееся отверстие. В одной половине сосуда содержится m=10,0 г водорода. Вторая половина откачана до высокого вакуума. Отверстие в перегородке открывают, и газ заполняет весь объем. Считая газ идеальным, найти приращение его энтропии.

Решение. Расширение газа здесь является необратимым процессом. Поэтому было бы ошибкой применить для данного процесса формулу

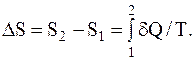
Воспользуемся тем, что энтропия – функция состояния и ее изменение полностью определяется начальным и конечным состояниями системы, независимо от того процесса, в ходе которого система перешла из начального состояния в конечное. Поэтому представим такой процесс расширения газа, который переводил бы его в то же самое конечное состояние, но являлся бы обратимым процессом. Найдя по вышеприведенной формуле приращение энтропии в таком обратимом процессе, мы решим поставленную задачу.

Так как данный газ изолирован от окружающей среды (Q=0, A=0), то его внутренняя энергия U, как это следует из первого начала термодинамики, должна оставаться постоянной. При этом будет постоянной и температура идеального газа во время его расширения. Значит, в качестве обратимого процесса, переводящего газ в то же конечное состояние, что и данный процесс, можно рассматривать процесс обратимого изотермического расширения, в ходе которого объем газа увеличивается в два раза. Так как в этом процессе T=const, DU=0 и, следовательно, Q=A.

Работа, совершаемая газом при изотермическом процессе, определяется соотношением

A=(mRT/m)×ln(V₂/V₁).

Таким образом, для изменения энтропии имеем

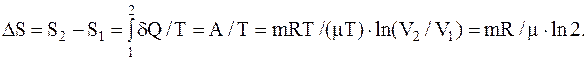
Выразим входящие в формулу величины в единицах СИ:

m=1,00×10^-3 кг, m=2,00×10^-3 кг/моль, R=8,3 Дж/(моль×К).

Выполнив вычисление, получим

DS=29 Дж/К.

4.6. Кислород, масса которого m=200 г, нагревают от температуры t=27 ^oС до температуры t=127 ^oС. Найти изменение энтропии, если известно, что начальное и конечное давления одинаковы и близки к атмосферному.

Решение. По условию задачи кислород в данном случае подчиняется уравнениям идеального газа.

Характер процесса нагрева неизвестен. Но изменение энтропии системы при переходе из одного состояния в другое определяется только параметрами этих состояний и не зависит от характера процесса.

Найти изменение энтропии можно, рассмотрев произвольный обратимый процесс, в результате которого систему (в данном случае идеальный газ) можно перевести из какого-либо состояния 1 в 2, совершив изобарное расширение. Кроме того из состояния 1 в состояние 3, совершив изотермическое расширение, а затем, последующим изохорным нагреванием из состояния 3в состояние 2. Тогда при переходе системы из состояния 1 в состояние 2 по первому пути, изменение энтропии системы можно определить по формуле

,

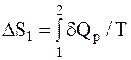где dQ_p=mC_pdT/m.

Изменение энтропии системы при переходе из состояния 1 в 2 по второму пути, равно сумме изменения энтропии при переходе из состояния 1 в состояние 3 и из состояния 3в состояние 2, т.е.

,

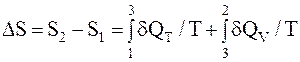где dQ_T=dA=pdV, dQ_V=mC_VdT/m.

При изобарном процессе – C_p=(i+2)/2,

где i – число степеней свободы.

Имеем

DS=S₂–S₁=m(i+2)R/2m×ln(T₂/T₁).

Легко проверить, что результат не изменится и при переходе 1 – 3 – 2.

Подставляя выражения dQ_T и dQ_V с учетом того, что при изотермическом процессе p=p₁V₁/V=mRT₁/(mV), получим

DS=mR/m×ln(V₃/V₁)+mC_V/m×ln(T₂/T₃).

Учитывая, что T₃=T₁, V₃=V₂, T₂/T₁=V₂/V₁ и (R+C_V)=C_p, получим

DS=S₂–S₁=m (i+2)R/2m×ln(T₂/T₁).

Подставив значения величин в единицах системы СИ, произведя вычисление, имеем

S=52 Дж/К.

4.7. Теплоизолированный сосуд, разделенный на две разные части (V₁=2 л, V₂=3 л), наполнен идеальным газом. В первой части газ находится под давлением p₁=10⁵ Па и температуре t₁=27 ^oC; во второй части под давлением p₂=5×10⁵ Па и той же температуре. Найти изменение энтропии всей системы после удаления перегородки и установления равновесного состояния. Изменится ли ответ, если в объемах V₁ и V₂ находятся разные газы?

Решение. Рассматриваемая система изолирована – теплообмен не происходит, внешние силы не действую. После удаления перегородки начнется заведомо необратимый самопроизвольный процесс, в результате которого во всемсосуде будет находиться однородный газ под некоторым давлением p₀, причем p₁<p₀<p₂. Вся система не участвует в теплообмене, ни один из газов не совершает работы. Следовательно, в конечном состоянии суммарная внутренняя энергия системы, а значит, и средняя энергия, приходящаяся на долю одной молекулы, будут такими же, как и до удаления перегородки. Поэтому температура газа остается постоянной и равной T₁.

Энтропия системы в результате этого необратимого процесса увеличивается. Изменение ее определяется только начальным и конечным состояниями системы. Чтобы найти это изменение, надо представить себе любой обратимый процесс, переводящий данную систему из начального состояния в конечное.

Представим себе, что сосуд разделен поршнем, который перемещается до тех пор, пока давление с обеих его сторон не станет одинаковым и равным p₀ (газ в левой части сосуда сжимается, в правой – расширяется). Чтобы процесс был изотермическим и обратимым, во – первых, должна быть нарушена теплоизоляция сосуда: газ в левой части сосуда должен отдавать теплоту, в правой – получать. Во вторых, поршень должен двигаться медленно, следовательно, на него должна действовать внешняя сила, компенсирующая результирующую силу давления газов.

После выравниваниядавлений обе части газа окажутся в одинаковых равновесных состояниях; поэтому если убрать перегородку (поршень), то энтропия системы не изменится. Следовательно, искомое изменение энтропии системы равно сумме изменений энтропии каждой части газа в отдельности при описанном изотермическом перемещении поршня:

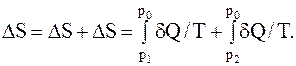
При изотермическом процессе

dQ_T=dA_T=p×dV=-V×dp.

Последнее из равенств следует из того, что d(pV)=0 при pV=const.

Тогда

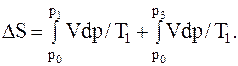
Выражая в интегралах текущий объём из уравнений изотермических процессов, записанных для начального и текущего состояний, получим

DS=(p₁V₁×ln(p₁/p₀)+p₂V₂×ln(p₂/p₀))/T₁.

Давление p₀ может быть найдено из уравнений изотермических процессов для каждой части газа:

p₁V₁=p₀V'₁; p₂V₂=p₀V'₂,

где V₁' и V₂' – объем каждой части газа после выравнивания давлений, причем V'₁+V'₂=V₁+V₁.

Тогда почленное сложение уравнений дает:

p₁V₁+p₂V₂=p₀(V₁+V₂),

откуда

p₀=(p₁V₁+p₂V₂)/(V₁+V₂).

Следовательно, для полного изменения энтропии будем иметь:

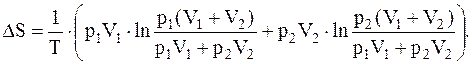
Выразив все величины в единицах СИ, подставив их значения, произведем вычисление

S=1,1 Дж/К.

Если бы в объемах V₁ и V₂ находились разные газы, то после удаления перегородки, даже при условии, что по обе стороны газы находятся под одинаковым давлении p_o, начнется необратимый самопроизвольный процесс диффузии, который приведет к выравниванию концентраций каждого из газов во всем объеме сосуда. Очевидно, что в процессе диффузии энтропия будет возрастать. Следовательно, в этом случае полное изменение энтропии системы больше значения, найденного ранее.

Чтобы рассчитать изменение энтропии в процессе диффузии, надо заменить реальный необратимый процесс таким воображаемым обратимым процессом, который приведет систему в то же самое конечное состояние. Такой процесс может быть осуществлен только с помощью полупроницаемых перегородок, т.е. перегородок, проницаемых для молекул одного газа и непроницаемых для молекул другогогаза.

4.8. Очень небольшой теплоизолированный сосуд разделен на две равные части теплопроницаемой перегородкой. В каждой части находится углекислый газ в количестве 10 моль. Температура газа в одной части сосуда t=28 ^oС, во второй части t=27 ^oС. Пренебрегая теплоемкостью сосуда, определить, во сколько раз возрастает вероятность системы при выравнивании температур? Определить изменение вероятности при переходе теплоты от менее нагретой части газа к более нагретой. Считать, что газ идеальный.

Решение. Согласно соотношению Больцмана, изменение энтропии прямо пропорционально натуральному логарифму вероятности W данного состояния системы:

DS=S₂-S₁=k×ln(W_2/W₁),

откуда

W₂/W₁=exp(DS/k),

где k – постоянная Больцмана;

W – термодинамическая вероятность состояния – число, пропорциональное количеству тех физически различных микросостояний системы, которыми может быть реализовано данное макросостояние.

Для того чтобы найти изменение энтропии, следует рассмотреть квазистатический процесс, который может перевести систему из начального состояния в конечное. Поскольку объем газа, находящегося в каждой части сосуда, остается постоянным, таким процессом может быть квазистатическое изохорное нагревание одной части газа и квазистатическое изохорное охлаждение другой части. Причем каждыйиз этих процессов должен происходить в результате теплообмена с внешними термостатами при нарушении теплоизоляции системы.

Если температура газа, находящегося в первой части сосуда, изменяется от T₁ до T'₁, а во второй части – от T₂ до T'₂, то

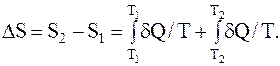
где dQ=mC_VdT/m;

m/m – число молей;

C_V=iR/2 – молярная теплоемкость при постоянном объеме;

i=6 – для углекислого газа.

Поскольку температура каждой частигаза изменяетсяне в результате теплообмена с внешнимитермостатами, ав результате перехода теплоты от одной части газа к другой, то количество теплоты, отдаваемое одним газом, равно количеству теплоты, получаемому другим газом. (Теплоемкостью сосуда, а, следовательно, и количеством теплоты, им получаемым, можно пренебречь). Так как в обеих частях сосуда находится однородный газ одинаковой массы, то изменение температуры по модулю будет также одинаковым. Если в результате теплообмена температура газа в первой части сосуда уменьшится, так что T₁=T₁-DT, то во второй части температура увеличится и T₂'=T₂+DT. При выравнивании температур T₁'=T₂' имеем

DT=(T₁–T₂)/2.

Подставив полученное соотношение в выражение для полного изменения энтропии, после интегрирования получим

DS=mC_V/m×(ln(1-DT/T₁)+ln(1+DT/T₂)).

Поскольку DT<<T₂, натуральные логарифмы можно разложить в степенной ряд и ограничиться только первыми членами. Тогда

DS=mC_VDT/m×(-1/T₁+1/T₂),

где mC_VDT/m=Q₁₂ – абсолютное значение количества теплоты, отданное одной и полученное второй частями газа. Следовательно, полученное выражение может быть использовано для расчета изменения энтропии не только при выравнивании температур, но при любом теплообмене между газами, находящимися в разных частях сосуда. В этом случае могут изменяться Q₁₂ и знак перед скобкой. Если Q₁₂ – количество теплоты, которое отдает менее нагретый, а получает более нагретый газ, то выражение, стоящие в скобках, полученного соотношения, примет вид (1/T₁-1/T₂).

В случае выравнивания температур, при DT=0,5 К, Q₁₂=1,25× 10^-7 Дж:

DS=1,38×10^-12 Дж/К, а W₂/W₁=exp(10¹¹).

Изменение энтропии при переходе такого же количества теплоты от газа менее нагретого к газу более нагретому

DS'=-1,38×10^-12 Дж/К и соответственно W₂'/W₁=1/exp10¹¹ ~ 10 ^{– 48}.

Полагая, что термодинамическая вероятность равна или прямопропорциональна числу случаев, когда данное состояние имеет место, полученный результат можно интерпретировать так: описанная в задаче система самопроизвольно переходит в состояние, при котором температуры газов будут равны практически всегда; переход теплоты от менее нагретого газа к более нагретому невозможен.

Однако если рассматривать вероятность перехода количества теплоты на много порядков меньше, например Q₁₂=1,25×10^-17 Дж, то в этом случае изменение энтропии при передаче теплоты от более нагретого газа к менее нагретому DS=1,38×10^-22 Дж/К и W₂'/W₁=е¹⁰ ~ 2×10⁴.

Изменение энтропии при переходе этого же количества теплоты от менее нагретого газа к более нагретому DS'=-1,38×10^-22 Дж/К и W'₂/W₁=e^-10=1/2×10⁴. Это значит, что уже в одном случае из 2×10⁴ возможен процесс перехода теплоты от менее нагретого газа к более нагретому, т.е. вероятность такого процесса резко повышается.

Очевидно, для того чтобы передача такого количества теплоты (порядка 10^-17 Дж) могла хоть сколько-нибудь изменить температуру газа, количество газа должно быть резко уменьшено. Так, для изменения температуры на 0,01 градуса число молей газа должно составлять 10^-15¸10^-16, что соответствует общему количеству молекул N=10⁸¸10⁷. Для макроскопических объемов, содержащих такое количество молекул, уже можно говорить о реальной вероятности процесса, идущего в нарушение второго начала термодинамики.