nbsp;   С учетом этого получаем

Не приводя промежуточных преобразований, выполним ана­лиз формулы (3.9), связывающей пористость с технологическими факторами. Она получена для следующих условий. Отливка представляет собой плиту, высота которой значительно больше толщины (H₀ >> 2R). Положение фронта солидуса определялось уравнением x_c = R - 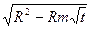. Распределение температур по сечению двухфазной зоны принято линейным. Расчетная схе­ма приведена на рис. 3.15.

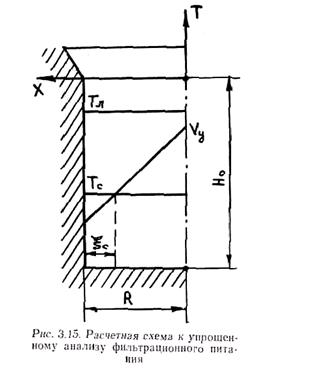
Предлагаем студентам вывести формулу (3.9) на индивидуаль­ных занятиях под руководством преподавателя.

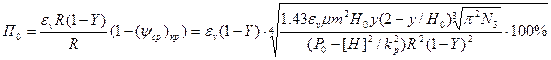
где П₀ — пористость, отнесенная ко всему объему отливки; Y = x_c (t = t_л)/R — относительная толщина затвердевшей корки в момент снятия перегрева в центре отливки.

Очевидно, что с увеличением Y, т. е. при более последова­тельном затвердевании и меньшей ширине жидкотвердой зоны, пористость уменьшается. Поэтому все мероприятия, приводящие к уменьшению ширины жидкотвердой зоны, снижают уровень пористости отливок. Возрастание скорости затвердевания (уве­личение коэффициента m) приводит к росту пористости отливки. Однако увеличение m приводит к росту Y. Поэтому влияние m может быть неоднозначным. Измельчение кристаллической струк­туры, если это не сопряжено с принятием соответствующих мер, приводит к росту пористости (увеличение N_з).

Важным технологическим фактором является повышение дав­ления на расплав Р₀, приводящее к снижению в нем содержания водорода. С уменьшением толщины стенки отливки R усложня­ются условия фильтрационного питания и увеличивается пори­стость отливок. Очевидно, что по мере удаления от прибыли (увеличение у) пористость увеличивается.

В реальных условиях картина фильтрационного питания зна­чительно сложнее. Фильтрационный поток сплава развивается раньше, чем в осевой части отливки будет снят перегрев. До это­го момента в центральной зоне отливки имеется жидкий сплав, который через междендритные каналы может фильтроваться в направлении фронта солидуса под действием перепада давлений, природа которого описана выше. При этом процесс кристаллиза­ции сплава сопровождается движением в сторону фронта кри­сталлизации междендритной жидкости. Условия питания на этой стадии облегчены наличием в центре отливки жидкого сплава. Они существенно затрудняются при смыкании фронтов ликвидуса в центре отливки. При этом питающий расплав может поступать только из прибыли, т. е. длина фильтрационного пути значитель­но увеличивается.

Наиболее благоприятные условия создаются при заполнении формы и питании отливки из тигля через металлопровод, как это осуществляется при литье вакуумным всасыванием, под низким давлением и с противодавлением. При этих методах в верхней части металлопровода имеется достаточное количество жидкого расплава и, кроме того, есть возможность значительно повысить перепад давлений на расплав. Как показали исследования, про­веденные при литье с противодавлением на алюминиевых спла­вах, при обычных условиях в отливках практически отсутствовала усадочная раковина, но наблюдалась значительная пористость. При увеличении перепада давлений до 0,3 МПа начинает вы­являться концентрированная усадочная раковина и уменьшается пористость. При перепаде давлений 0,5 МПа пористость исчезает практически полностью. Дальнейшее повышение давления до 2,5 МПа не изменило характера усадочных дефектов, но несколь­ко сместило усадочную раковину вверх. Следует отметить, что при значительном (до 2,5 МПа) повышении всесторонне действу­ющего газового давления получаются практически бездефектные отливки, но боковые и верхние поверхности вдавливаются внутрь, что искажает конфигурацию отливки.

Фильтрационному режиму питания предшествует режим так называемого суспензионного питания. Известно, что перегретые жидкие сплавы подчиняются реологическому закону ньютонов­ской жидкости и обладают неограниченной способностью к те­чению. Именно поэтому не возникает проблем с компенсацией объемной усадки в жидком состоянии. Как было показано в разд. 1, это относится к сплавам при температурах ниже темпе­ратуры ликвидуса, доля твердой фазы в которых не превышает 8—10%. При большем количестве твердой фазы изменяется реологическая природа сплавов и для их течения требуется выпол­нение условия t > t_s, где t — касательные напряжения, создавае­мые внешними силами; t_S — предельное касательное напряже­ние сдвига для сплава. Так как с увеличением доли твердой фазы в расплаве с понижением его температуры ts увеличивается, рано или поздно компенсация усадки за счет перемещения метал­лической суспензии как единого целого прекратится. При этом произойдет образование жесткой структуры суспензии, которая при дальнейшем охлаждении отливки ведет себя как капилляр­но-пористое тело, и компенсация усадки осуществляется рассмот­ренным выше фильтрационным путем.

Нарушение условия t > t_s происходит при некотором крити­ческом содержании твердой фазы y_кр, которое зависит от приро­ды сплава и давления, прилагаемого к отливке в процессе ее формирования. Температура сплава, соответствующая доле твердой фазы y_кр, называется температурой нулевой жидкотекучести.

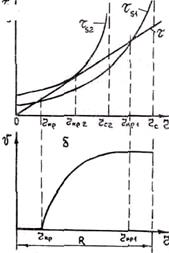
Рис. 3. 16 Зависимость t, t_S (a) и v (б) от расстояния r до центра отливки

На рис. 3.16 показано распределение величины предельного ка­сательного напряжения сдвига ts и касательного напряжения t, создаваемого активными силами, внутри жидкотвердой зоны в центре отливки (0 £ r < r_с, где r_с — радиальная координата фрон­та солидуса). Так как с увеличением r уменьшается температура сплава и увеличивается доля твердой фазы y, то величина ts по мере удаления от оси отливки резко возрастает. Видно, что при r_кр1 > r > r_кр t > t_s. Поэтому в этой зоне dv/dx ¹ 0. В области r_кр1 < r <r_с мо­жет осуществляться только фильтрационное питание. На рис. 3.16, б по­казано распределение скорости суспензионного питания. В зоне r_кр1 < r < R имеет место стержневое те­чение (dv/dx = 0).

При затвердевании фронт солидуса перемещается к центру отливки, а кривая ts смещается вверх и влево. В некоторый момент кривая ts зай­мет положение t_S2 (рис. 3.16, a), a фронт солидуса — r_с2. При этом t < ts для всей жидкотвердой зоны (0 < r <r_с2). Поэтому с данного мо­мента времени прекратится суспензионное питание.

Очевидно, что за счет этапа суспензионного питания уменьшается ширина зоны фильтрационного питания, так как r_с2 < r_с(t = t_л}, где t_л — время снятия перегрева в центре отливки. Подставив в формулу (3.10) вместо 1 – У = 1 - xc(t = t_л}/R величину r_с2/R, получим выражение для определения пористости отливки

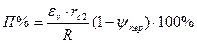
Так как r_с2 < r_с(t = t_л}, то очевидно, что за счет суспензионного питания пористость уменьшается.

Влияние суспензионного питания на процесс компенсации объ­емных усадочных дефектов для разных сплавов и условий раз­лично. Например, структурирование алюминиевых сплавов про­исходит при температурах, очень близких к температуре ликвиду­са. Поэтому роль суспензионного питания при формировании отливок из этих сплавов очень незначительна. Учет суспензион­ного питания связан с математическим описанием движения жидкотвердой фазы как B-тела, закономерности которого рас­смотрены в курсе «Основы литейной гидравлики и теплофизики».

Следует отметить, что с ростом прилагаемого к отливке перепада давлений Р₀ влияние суспензионного питания на уменьшение по­ристости отливок увеличивается.

Анализу математической модели совместного действия сус­пензионного и фильтрационного питания должно быть посвящено несколько практических занятий.

3.3.4. МЕТОДЫ БОРЬБЫ С ОБЪЕМНЫМИ УСАДОЧНЫМИ ДЕФЕКТАМИ. РАСЧЕТ И КОНСТРУИРОВАНИЕ ПРИБЫЛЕЙ

Практические меры борьбы с усадочными дефектами в отлив­ках основываются на изложенных выше теоретических положениях. Основными направлениями в устранении

усадочных дефек­тов являются: установка над каждым термическим узлом при­были и оптимизация тепловых и гидродинамических условий пи­тания отливки из прибыли. При этом конфигурация отливки и тепловые условия ее затвердевания должны отвечать условиям принципа направленного к прибыли затвердевания. Прибыль — дополнительный объем сплава, имеющий соответствующие раз­меры и конфигурацию, в который в процессе питания отливки выводятся усадочные дефекты. Расположена прибыль на терми­ческом узле отливки. После охлаждения отливки прибыль уда­ляется (отрезается или отламывается) и передается на переплав­ку. Так как установка прибылей увеличивает расход сплава на изготовление отливки, нужно применять меры, направленные на повышение эффективности ее работы и снижение объема. Эффек­тивность использования жидкого сплава характеризуется выходом

годного (ВГ). Он равен отношению черновой массы отливки М_отлк массе жидкого сплава, залитого в форму, М_ж:

ВГ = M_ОТЛ × 100%/M_Ж

При этом М_ж = М_отл + М_л.с + М_пр, где М_л.с — масса литниковой системы; М_пр — масса прибылей.

Эффективность работы прибылей зависит от их расположения, размеров и конфигурации, тепловых и гидродинамических усло­вий.

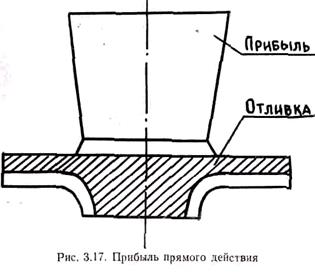
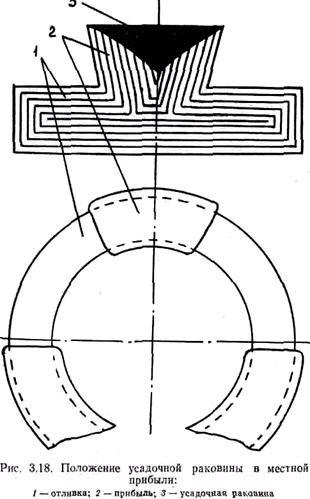
По направлению питания прибыли разделяются на прямые, местные и боковые. Прямые прибыли располагаются непосред­ственно над всем питаемым узлом (рис. 3.17). Так как сплав, компенсирующий усадку, подается при этом в отливку из при­были по кратчайшему пути, то условия питания наиболее благо­приятны. Недостатком прямых прибылей, если они устанавлива­ются, например, по всему периметру кольцевой отливки, является большой расход металла на прибыли. С целью экономии металла можно устанавливать вместо одной сплошной прибыли несколько местных прибылей. Как видно из построенных изосолид (рис. 3.18), местные прибыли, если их установить друг от друга на некотором максимально допустимом расстоянии, обеспечивают хорошее пи­тание отливки.

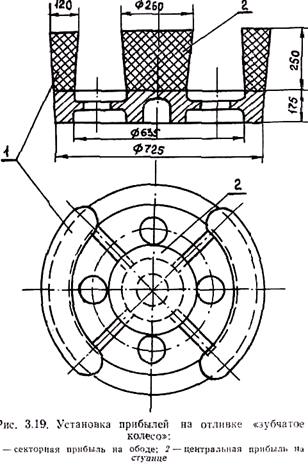
При применении местных прибылей прямое питание получа­ют только части отливки, находящиеся непосредственно под при­былями (рис. 3.18). Части, находящиеся между прибылями, полу­чают уже не прямое питание, а боковое. При этом различного рода включения не могут всплыть в прибыль. Поэтому на верхней поверхности необходимо предусматривать повышенные припуски на механическую обработку. Обычно суммарная длина местных секторных прибылей на отливках типа колес (рис. 3.19) состав­ляет не менее 1/3и не более 2/3 от периметра отливки.

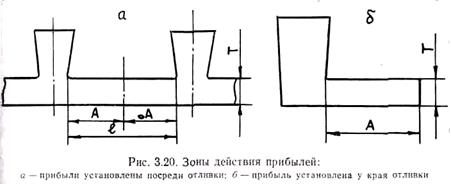
Местные прибыли обеспечивают питание примыкающих к ним участков отливки на определенную длину, называемую зоной дей­ствия прибыли. Зоны действия прибылей определяют на основа­нии эмпирических данных в зависимости от толщины питаемого узла (рис. 3.20). Например, для прибылей, установленных по схеме рис. 3.20, а, зона действия прибыли для сплава латуни рав­на А = 4Т, для силуминов А = 3Т. Вследствие влияния концевого эффекта (нарастание твердой корки на торцевой поверхности отливки) зона действия прибыли, установленной у края отливки (рис. 3.20, б), увеличивается и равна для латуни А = 5Т, а для силумина А = 6,5Т. Таким образом, расстояние между местными прибылями l не должно превышать удвоенную величину зоны действия прибыли, т. е. l £ 2А. Если l > 2A, то в зависимости от характера затвердевания сплава за пределами зоны влияния при­былей в отливках будут образовываться усадочные дефекты в виде раковин или усадочной пористости.

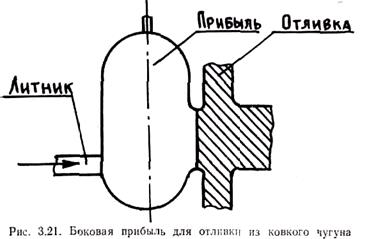
Для протяженных отливок с большим отношением длины к толщине или ширине целесообразно применять боковые прибыли (рис. 3.21). Боковые прибыли применяют также при изготовлении отливок из сплавов, плохо обрабатывающихся резанием (сталь 110Г13Л, ковкий чугун и т. п.).

Преимущества боковых прибылей по сравнению с верхними сводятся к возможности питания меньшими по объему прибы­лями протяженных отливок, снижения трудоемкости удаления прибылей от отливок (их можно отламывать или отрезать при значительно меньшей площади резки), уменьшения трудоемкости механической обработки подприбыльных участков отливки и т. д. Место соединения боковой прибыли с отливкой называется шейкой прибыли. Следует отметить, что шейка прибыли может иметь приведенную толщину стенки, существенно меньшую, чем у отливки. Это объясняется влиянием прогрева формы около шейки прибыли протекающим через нее металлом, так как залив­ка в данных случаях осуществляется через прибыль (см. рис. 3.21). К моменту окончания заливки температура формы около шейки прибыли наибольшая и убывает по мере удаления от прибыли, что способствует направленности затвердевания.

Иногда боковые прибыли устанавливают на термических уз­лах отливки, расположенных на разной высоте. Такие прибыли называют потайными (рис. 3.22).

Для того чтобы прибыль работала так, как показано на рис. 3.22, необходимо обеспечить в ней некоторый баланс давле­ния жидкого металла. Потайные прибыли являются закрытыми. Поэтому с момента образования на их поверхностях достаточно прочной корки затвердевшего металла жидкий расплав отсекает­ся от внешнего атмосферного давления. Вследствие действия ат­мосферного давления со стороны открытой прибыли и увеличиваю­щегося к низу отливки гидростатического давления, равного, например, для нижней прибыли rgH_н, перепад давлении будет направлен вверх, т. е. он будет обеспечивать перенос металла в прибыль, а не из прибыли в отливку. В этом случае установка потайных прибылей приведет к увеличению объема верхней при­были, так как она должна компенсировать дополнительно усадку сплава в этой прибыли. Прибыли начнут действовать только после затвердевания сечений В — В и А — А.

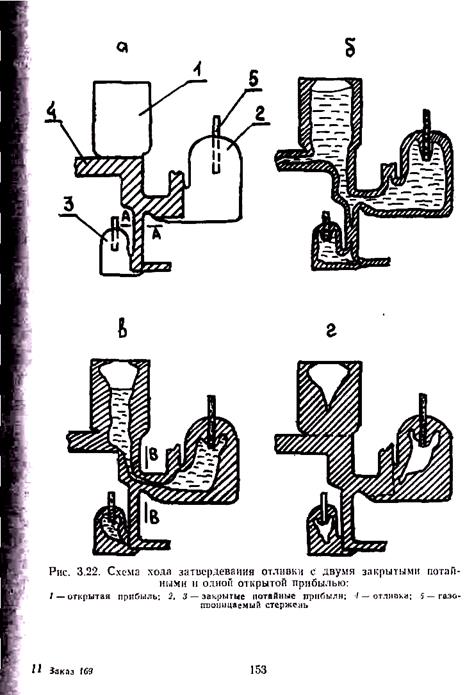
Для улучшения действия прибылей в них устанавливают газо­проницаемые стерженьки, передающие внутрь прибыли атмосфер­ное давление (см. рис. 3.22). Однако гидростатическое давление rgH_н и rgH_с. в этом случае все равно оказывается некомпенсированным. Для обеспечения нужного баланса давлений целесооб­разно создать в прибылях повышенное газовое давление, равное для нижней и средней прибыли соответственно Р_а + rgH_н и P_a. + rgH_с. В этом случае все прибыли с самого начала будут действовать независимо: каждая будет питать свой узел.

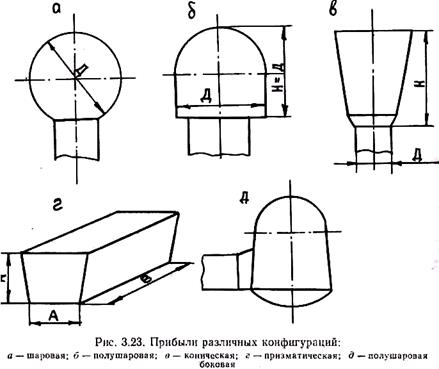
По конфигурации различают шаровые или полушаровые, ци­линдрические, конусные, овальные, прямоугольные прибыли (рис. 3.23).

С точки зрения тепловых условий работы конфигурация при­были должна обеспечить при данном ее объеме минимальную поверхность охлаждения. Известно, что этому условию удовлет­воряет шар. Однако такие прибыли сложно выполнить в форме, поэтому наиболее широко применяют полушаровые закрытые прибыли или конические открытые прибыли. Часто используют прибыли, имеющие овальное горизонтальное сечение. Следует за­метить, что при конструировании прибылей их конфигурация всегда увязывается с конфигурацией питаемого узла. Более де­тально вопросы конструирования прибылей изучаются в техно­логических курсах.

Рассмотрим основные принципы расчета прибылей. Прежде всего, прибыль должна иметь запас сплава, обеспечивающий ком­пенсацию объемной усадки отливки и самой прибыли. Так как в процессе формирования отливки на стенках прибыли происходит образование затвердевшей корки, то объем прибыли равен

V_ПР = V_УС.Р + V_З.К

V_УС.Р = e_V(V_ОТЛ + V_ПР)

где V_yc.p — объем усадочной раковины; V_з.к — объем затвердев­шего сплава в прибыли. Объем затвердевшего металла зависит от тепловых условий работы прибыли и гидродинамических усло­вий, определяющих скорость опускания сплава в прибыли. Чем больше интенсивность теплоотвода от прибыли и чем меньше ско­рость опускания уровня сплава в ней, тем больше V_з.к. Как сле­дует из полученного в предыдущем разделе уравнения неразрыв­ности потока питающего жидкого сплава, скорость опускания сплава в прибыли непосредственно связана со скоростью выделе­ния в расплаве отливки твердой фазы dy/dt. Чем больше dy/dt, тем с большей скоростью может опускаться сплав в прибыли.

Однако эта потенциальная возможность в зависимости от ха­рактера затвердевания используется в разной степени. При после­довательном затвердевании, за исключением питания осевых участ­ков отливки, жидкий расплав полностью и практически мгновен­но компенсирует появившийся в отливке дефицит питания. При объемном затвердевании в условиях фильтрационного и суспензионного питания скорость питающего потока существенно за­висит от прилагаемого к расплаву давления. Если давление не­достаточно велико, то, несмотря на наличие дефицита питания, расплав из прибыли не будет израсходован. При этом в отливке образуется большая усадочная пористость.

Коэффициент полезного использования металла в прибыли — b = V_yc.p/V_пp. Здесь, строго говоря, в величину V_yc.p следует вклю­чать весь дефицит питания, а не только собственно объем усадоч­ной раковины. Величина b зависит от конфигурации прибыли, прилагаемого к расплаву давления и тепловых условий работы при­были. Для обычных открытых прибылей b = 0,1, для закрытых прибылей b = 0,11 — 0,15, для прибылей с газовым давлением b = 0,13 ¸ 0,2. Применение подогрева сплава в прибылях позво­ляет значительно повысить b и снизить расход металла на при­были. Если принять, что коэффициент b известен, то можно рас­считать объем прибыли по простой формуле, впервые полученной И. Пржибылом:

V_УС.Р = e_V(V_ОТЛ + V_ПР)

V_УС.Р = bV_ПР

bV_ПР = e_VV_ОТЛ + e_VV_ПР

Отсюда V_ПР(b - e_V) = e_VV_ОТЛ или

V_ПР=e_VV_ОТЛ/(b-e_V)

Здесь V_отл — объем узла отливки, питаемого данной прибылью. Высота прибыли принимается равной ее диаметру или несколько больше.

Классический метод расчета прибылей сводится к определе­нию глубины проникновения усадочной раковины в системе от­ливка — прибыль. Высоту прибыли устанавливают, исходя из обеспечения полного расположения усадочной раковины в при­были с некоторым запасом.

В основе математического расчета прибылей на ЭВМ лежит балансный принцип расхода сплава из прибыли на питание и затвердевание на ее стенках (см. гл. 6.3 и 6.4) при определении контура усадочной раковины. Кроме балансного уравнения мо­дель включает дифференциальные уравнения, описывающие кине­тику затвердевания сплава в отливке и прибыли. Навыки машин­ного расчета прибылей студент должен получить на практических занятиях.

Приведенная формула (3.12) получена для плоской отливки толщиной 2Ro при следующих допущениях:

1) фронт солидуса в отливке продвигается по закону , а В Прибыли

2) толщина прибыли равна 2R_п > 2R₀;

3) вся усадка приведена к температуре солидуса и включает усадку в жидком состоянии и при затвердевании.

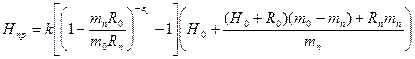
где A—коэффициент запаса (обычно k = 1,5 ¸ 3). Как правило, отношение приведенных размеров прибыли и отливки принимают в пределах R_п/R₀ = 1,15 ¸ 1,5.

Выполним расчет высоты прибыли для стальной отливки: R_п/R₀ = 1,25; R₀ = 15 см; R_п = 18,75 см; e_V = 0,06; высота отливки H₀ = 40 см; m₀ = 0,085 cм/с^1/2 ; m_п = 0,060 cм/с^1/2.

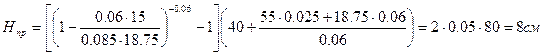
Для того чтобы уменьшить m_п по сравнению с m₀, необходимо применить подвод сплава в прибыль, использовать смесь с мень­шим коэффициентом аккумуляции тепла, а для крупных отливок осуществить доливку металла в прибыль из ковша. В условиях рассмотренного примера при m_п = m₀ = 0,085 высота прибыли равна H_пр = 2×0,11×95 = 21 см. Видно, что уменьшение интенсив­ности затвердевания сплава в прибыли приводит к уменьшению объема прибыли.

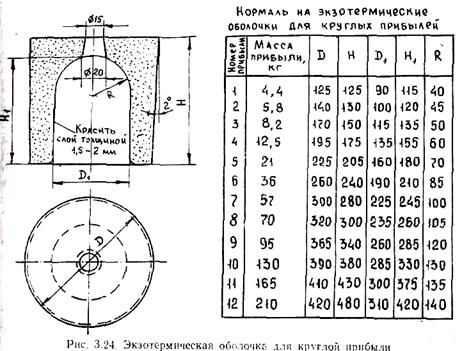
Существенного уменьшения затвердевшего в прибыли сплава, а следовательно, и необходимого ее объема можно добиться, при­меняя обогрев прибылей экзотермическими смесями. Из этих сме­сей изготовляют стаканы или втулки, которые устанавливают в прибыльные части полости формы (рис. 3.24).

Существуют различные по составу экзотермические смеси. Экзотермическая реакция, сопровождающаяся большим выделе­нием тепла, представляет собой реакцию восстановления окиси железа алюминием (алюмотермия) или кремнием (силикотермия):

Fе₂О₃ + 2Аl = Аl₂O₃ + 2Fe + Q₁,

2Fе₂О₃ + 3Si = 3SiO₂ + 4Fe + Q₂.

Кроме алюминиевого порошка, ферросилиция и окалины смесь содержит связующее для придания ей прочности во влажном со­стоянии и после сушки, а также древесные опилки, гипс, моло­тый шамот, глину для обеспечения газопроницаемости смеси и регулирования интенсивности экзотермической реакции.

Расчет экзотермических прибылей сводится к определению номера нормализованной экзотермической оболочки для оформле­ния прибыли. Подбор оболочек осуществляют по массе прибыли m_пр. Массу прибыли находят по специально разработанным но­мограммам. Принципиально ее можно определить по приведенной выше формуле И. Пржибыла, приняв b = 0,2 ¸ 0,25, или а ис­пользованием полученной выше формулы для расчета высоты прибыли, приняв константу затвердевания в 1,5—2 раза мень­шей по сравнению с обычной песчаной формой. По массе прибыли находят размеры экзотермических оболочек по нормализованным таблицам (см., например, рис. 3.24).

Выше было сказано о большой роли в повышении эффектив­ности работы прибылей и их экономичности перепада давлений, действующего на кристаллизующийся расплав. Так, П. И. Ямшановьш были предложены прибыли с повышенным газовым давлени­ем, создаваемым диссоциацией при высоких температурах мела, карбоната магния или цинка:

СаСО₃ = СаО + СO₂ при Т ³ 825°С;

MgCO₃ = MgO + CO₂ при Т ³ 350°С;

ZnCO₃ = ZnO + CO₂ при Т ³ 300°С.

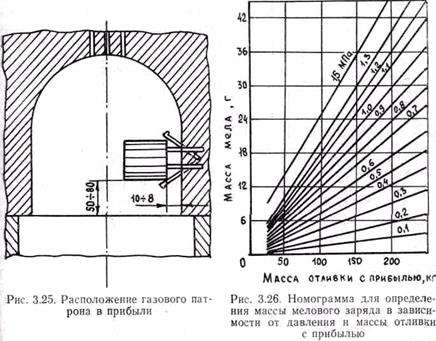
Определенная масса данных веществ помещается в специаль­ный патрон, устанавливаемый внутрь закрытой прибыли (рис. 3.25). Оболочки и крышки патронов изготавливают уплот­нением в металлических ящиках смесей, состоящих из глины, мо­лотого шамота и древесных опилок, добавляемых для повышения газопроницаемости оболочки. Оболочки сушат при 100 - 110 ⁰C и обжигают при 350 °С. Главное требование к оболочке сводится к тому, что ее толщина должна обеспечивать прогрев помещен­ного в нее наполнителя до температуры диссоциации не раньше, чем на стенках прибыли вырастет достаточно прочная корка за­твердевшего сплава, способная выдержать повышенное давление.

Параметры прибыли, патрона и массу заряда определяют по эм­пирически разработанным номограммам. Массу прибыли можно определить, например, по формуле И. Пржибыла, приняв в ней b = 0,13 ¸ 0,20.

В зависимости от массы прибыли и создаваемого давления по номограмме, приведенной на рис. 3.26, определяют массу мела, помещенного в патрон.

Толщину стенки патрона и его размеры определяют по специальным номограммам. Применение прибылей газового давления позволяет не только повысить выход годного, но и существенно снизить пористость отливок.

Детальное изучение методов расчета и конструирование при­былей для отливок из различных сплавов предусмотрено в соот­ветствующих технологических курсах. Приближенные аналитиче­ские и эмпирические формулы для расчета прибылей получены А. А. Рыжиковым, Б. Б. Гуляевым, Ф. Ф. Василевским, Н. Бишопом и В. Джонсоном, Р. Намюром и др. Главной особенностью этих методов является их ориентация на последовательно затвер­девающие сплавы и усадочные дефекты, проявляющиеся главным образом в виде усадочной раковины. Их применение к объемно затвердевающим сплавам неправомерно, так как усадочная рако­вина в этих случаях очень мала по объему по сравнению с объ­емом пор.

Методику расчета прибылей при объемном затвердевании спла­ва можно построить, исходя из следующих принципов:

1) прибыль должна быть достаточно теплоизолирована (на­пример, при кокильном литье стенки прибыльных частей оклеи­ваются листовым асбестом или по­крываются специальной краской). При этом должно выполняться условие: продолжительность снятия перегрева в центре прибыли должна быть не меньше продолжительности затверде­вания отливки;

2) объем прибыли должен быть достаточным для компенсации объем­ной усадки отливки и прибыли. Его можно найти по формуле и. Пржибыла, приняв, в ней b = 0,2 ¸ 0,25;

3) высота прибыли и прилагаемое к сплаву в прибыли давление Р₀должны обеспечить фильтрационное питание отливки, гарантирующее за­данный уровень пористости в ней. Дав­ление (Р₀ + rgH_п), обеспечивающее заданное значение пористости, в первом приближении можно найти с использованием формул, полученных в разд. 3.

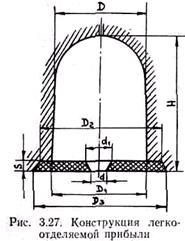
В заключение рассмотрим прибыли с облегченным отделени­ем от отливок (рис. 3.27).

Между прибылью и питаемым узлом устанавливают перего­родку в виде керамической пластины. Важнейшим требовани­ем является совпадение оси отверстия в перегородке с термиче­скими центрами прибыли и отливки. При нарушении этого требо­вания в отливке образуется усадочная раковина. Параметры пере­городки и размеры отверстия выбирают таким образом, чтобы она быстро прогревалась до температур, исключающих образо­вание на ее поверхностях затвердевшего металла. Обычно диа­метр прибыли определяют по формуле

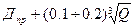
где d_вп — диаметр окружности, вписанной в термический узел пи­таемой отливки, дм; Д_пр — диаметр прибыли, дм; Q — масса пи­таемого узла, кг. Высоту прибыли принимают равной (1 ¸ 1,5)Дпр. Толщину пластины и диаметр отверстия в ней определяют в за­висимости от значения диаметра прибыли по соответствующим таблицам.

ГЛАВА 3.4. ЛИТЕЙНЫЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ В ОТЛИВКАХ

В предыдущей главе были рассмотрены явления, связанные с развитием в процессе формирования отливки объемной усадки. Пока сплав, имеющий температуру внутри интервала кристалли­зации, сохраняет характерную для жидкости текучесть, усадочные явления проявляются как объемные. Линейные размеры при этом определяются, как и у любой жидкости в условиях действия зем­ного тяготения, размерами сосуда, в котором она находится. В процессе охлаждения уменьшается только объем. Собственно линейная усадка, т. е. независимое уменьшение линейных раз­меров отливки при понижении ее температуры, начинает разви­ваться только после потери сплавом текучести в конкретных си­ловых условиях формирования отливки. По предложению И. И. Новикова, с этой точки зрения интервал кристаллизации сплава можно разбить на две зоны: жидкотвердую и твердожидкую. В жидкотвердой зоне (при Т_у < T £ T_л, где Т_у — темпера­турная граница частей) сплав сохраняет текучесть. При Т_c £ Т £ Т_у в твердожидкой зоне интервала кристаллизации в спла­ве содержится количество твердой фазы, необходимое для обра­зования каркаса, проявляющего свойство твердого тела сохранять ранее приданную ему конфигурацию. Эту нижнюю часть интер­вала кристаллизации А. А. Бочвар назвал эффективным интер­валом кристаллизации сплава (ЭИК). В пределах ЭИК. кристал­литы образуют остов отливки, но частично отделены друг от дру­га прослойками расплава. Так как при температуре Т < Т_у сплав теряет текучесть, то, начиная с Т = Т_у, в отливке будет происхо­дить линейная усадка. При Т > Т_у реализуется только объемная усадка.

3.4.1. ГОРЯЧИЕ ТРЕЩИНЫ В ОТЛИВКАХ

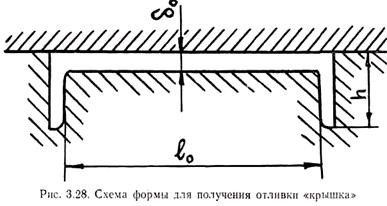
Если свободную линейную усадку отливки затормозить, то в ней возникнут напряжения растяжения. На рис. 3.28 показана схема формы для изготовления отливки «крышка». При темпера­туре Т = Т_у размер отливки l₀ равен размеру формы. Если участок формы между боковыми стенками отливки абсолютно податлив, то при охлаждении отливки до температуры Т произойдет ее пол­ная усадка и длина отливки будет равна l = l₀(1 - a_т(T_у - Т)). При этом никаких напряжений в ней не возникает. Если форма абсолютно неподатлива, то отливка сохранит размер l₀, т. е. ее длина будет больше того значения, которое она должна иметь при температуре Т, на величину Δl = l₀ – l = l₀ – l₀(1 - a_т(T_у - Т)) = l₀a_т(T_у - Т). Таким образом, отливка получит в данном слу­чае относительную деформацию растяжения e_у = Δl/l₀ = a_т(T_у - Т). Если форма обладает некоторой податливостью, то относительная деформация растяжения уменьшается на величину e_п, где e_п - относительная деформация формы за время усадки. Если учесть расширение участка формы между ребрами вследствие ее про­грева, то результирующая относительная деформация отливки будет удовлетворять равенству

e = e_У - e_П + e_Р

где e_р — относительная деформация формы вследствие ее тепло­вого расширения.

С уменьшением температуры внутри ЭИК увеличивается e_у и e_р, т. е. относительная деформация отливки e растет, достигая при Т = Т_с наибольшего значения e_mах = a_т(T_у - Т), если прене­бречь величинами e_п и e_р. В случае, если деформация растяжения отливки e превзойдет деформационную способность e₀, в отливке возникнет горячая трещина.

Таким образом, необходимое условие образования горячих тре­щин сводится к торможению свободной линейной усадки сплава во время его затвердевания в литейной форме. Достаточное усло­вие выражает неравенство e ³ e₀, т. е. образование трещин проис­ходит в момент превышения относительной деформацией сплава eего деформационной способности e₀. Таким образом, для образо­вания трещины необходимо, чтобы e_у - e_п + e_р ³ e₀.

Из этого неравенства вытекают следующие пути борьбы с горячими трещинами:

1) улучшение податливости форм, т. е. увеличение e_п;

2) совершенствование конструкции отливки с целью исклю­чения торможения линейной усадки;

3) синтез сплавов, обладающих низкими значениями отно­сительной линейной усадки (уменьшение a_т) и высокой дефор­мационной способностью e₀.

Комплекс конкретных технологических мероприятий, направ­ленных на исключение трещин в отливках, будет рассмотрен в конце данной главы.

Особое место среди данных мероприятий занимает повышение сопротивляемости сплавов образованию горячих трещин. Под термином «горячеломкость сплавов» понимают их технологическое свойство образовывать горячие трещины в отливках. Для определения этого свойства применяют различные технологические пробы (рис. 3.29). Горячеломкость сплава характеризуется зна­чением длины образца L₀, начиная с которой в отливках образу­ются трещины. Чем больше L₀, тем меньше сплав склонен к тре­щинам, т. е. тем меньше его горячеломкость.

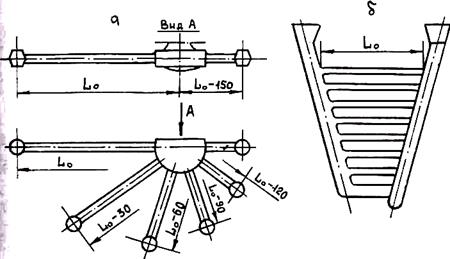
Рис. 3.29. Конструкции проб на горячеломкость сплавов:

a — проба А. Татюра; б — проба И. Н. Прохорова

Для примера можно привести так называемую кольцевую пробу, которая представляет собой кольцо, залитое в кокиль с металлическим стержнем. Показателем горячеломкости является отношение протяженности самой большой трещины к радиально­му сечению кольца, выраженное в процентах. Например, для спла­ва Аl — Si в зависимости от содержания кремния этот показатель изменяется в пределах от 10 до 50%. Часто для характеристики горячеломкости изготовляют из сплава несколько колец разной толщины (от 5 до 42,5 мм). Критерием горячеломкости в данном случае служит наибольшая толщина кольца, выраженная в мил­лиметрах, при которой образуется трещина. Чем меньше толщина кольца, тем меньше склонен сплав к горячим трещинам. Выбор той или иной пробы зависит от ее чувствительности для данной группы сплавов. Поэтому более подробно методика оценки горячеломкости сплавов будет рассмотрена в технологических курсах.

3.4.1.1. ТЕОРИЯ ГОРЯЧЕЛОМКОСТИ СПЛАВОВ

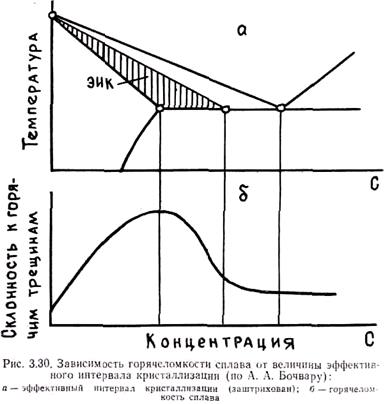
Одним из первых систематические исследования горячеломкости сплавов проводил А. А. Бочвар. По его мнению, горячеломкость сплавов связана с шириной ЭИК. С увеличением шири­ны ЭИК увеличивается склонность сплава к образованию горячих трещин (рис. 3.30).

В соответствии с теорией горячеломкости, разработанной Н. Н. Прохоровым, деформационная способность сплавов e₀ опре­деляется пластической деформацией растяжения сплавов e_пл в момент разрушения при температуре солидуса. Механизм обра­зования горячих трещин, по Н. Н. Прохорову, сводится к следующему. Расплав в эффективном интервале температур представ­ляет собой кристаллиты, отделенные друг от друга тонкими про­слойками жидкого сплава. Принятая Н. Н. Прохоровым упро­щенная схема строения сплава в ЭИК приведена на рис. 3.31.

При температуре Т_у начала свободной линейной усадки жидко-твердый расплав теряет свою подвижность как единое целое.

На схеме показаны кубические кристаллиты, разделенные друг от друга прослойками жидкого сплава. При полном торможении усадки размер l₀ остается в процессе охлаждения сплава постоян­ным. В процессе охлаждения сплава размер прослоек d будет уменьшаться. При этом, как было показано в разд. 2, вследствие объемной усадки кристаллизующейся жидкости ее давление бу­дет иметь тенденцию к уменьшению. Так как система лишена подвижности вдоль размера l₀, возможно лишь перемещение кри­сталлитов навстречу друг другу в перпендикулярном направле­нии под действием возникающего перепада давлений. При этом жидкий сплав из области вертикальных прослоек перемещается в область горизонтальных, компенсируя там объемную усадку. Подобный процесс развивается до полного исчезновения верти­кальных (в соответствии со схемой) прослоек (рис. 3.31, б).

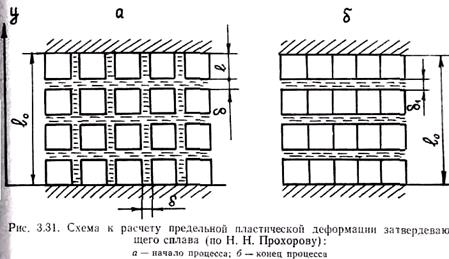
Дальнейшая усадка сплава будет сопровождаться порообра­зованием и формированием трещины. Н. Н. Прохоров для при­веденной на рис. 3.32 структуры сплава выполнил следующий вы­вод формулы для расчета его деформационной способности в ус­ловиях одноосного изотермического растяжения вдоль оси у. Объем жидкого сплава, приходящегося на один кристаллит в начале деформирования, равен (l + f)³ – l³. После деформиро­вания объем жидкости равен l²(l + f₁) – l³ Приравняв эти выра­жения, получим (l + f)³ = l²(l + f₁). Отсюда f₁ = 3f + 3f²/l + f³/l². Относительная деформация растяжения равна e_пл =(f₁ - f) / (1 + f) = f(2 + f/l)/l

Доля твердой фазы в сплаве при температуре Т равна

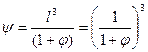
Отсюда получаем j/l = 1/y^1/3 - 1. С учетом этого

e_ПЛ = 1/j^2/3 – 1 (3.13)

Из формулы И. Н. Прохорова следует, что по мере снижения температуры уменьшается деформационная способность сплава e_пл, так как при этом доля твердой фазы y увеличивается. При температуре солидуса y = 1 и e_пл = 0.

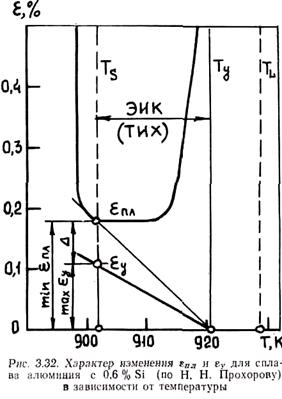
На рис. 3.32 приведен характер зависимости e_пл от темпера­туры внутри интервала кристаллизации, определенный экспери­ментально для сплава алюминия с 0,6 % Si. Здесь же приведена зависимость относительной свободной линейной усадки e_у от тем­пературы в соответствии с формулой e_у = a_тв(T_у - Т). Величину Δ = min (e_пл - e_у) Н. Н. Прохоров назвал запасом пластичности сплава, а интервал температур (Т_у - Т_c) — температурным интер­валом

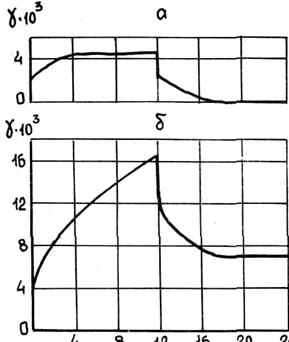
хрупкости (ТИХ). Видно, что в отличие от предсказывае­мого теорией Н. Н. Прохорова величина интер­валом при температуре солидуса не равна нулю и при дальнейшем охлаждении увеличива­ется. Многочисленные эксперименты показывают, что температур­ный интервал горячеломкости (ТИГЛ) не обязательно примыкает к температуре солидуса, а может иногда охватывать весь тем­пературный интервал хладноломкости.

Очевидно, что реальный механизм образования горячих тре­щин значительно сложнее рассмотренного выше. Прежде всего, кристаллиты имеют гораздо более сложное строение, чем пока­зано на рис. 3.31. Чаще всего они имеют вид разветвленных, сцепленных друг с другом дендритов. При нагружении происхо­дит не только рассмотренная выше циркуляция жидкого сплава, но и непосредственная деформация кристаллитов. Для выяснения вопроса о деформационной способности сплава необходимо уста­новить соответствующий его поведению реологический закон. Простейшие реологические модели были рассмотрены в разд. 1.

3.4.1.2. РЕОЛОГИЧЕСКАЯ МОДЕЛЬ СПЛАВА В ИНТЕРВАЛЕ КРИСТАЛЛИЗАЦИИ

Систематические исследования реологических свойств сплавов. в интервале кристаллизации были выполнены Г. Ф. Баландиным и Л. П. Каширцевым. На основе анализа экспериментальных дан­ных, полученных для алюминиевых сплавов, они установили, что реологическое поведение сплавов в интервале кристаллизации отвечает поведению сложного тела, состоящего из последователь­но соединенных тел Бингама и Кельвина, т. е. реологическая фор­мула сплава — Т = В - К. Тела Бингама и Кельвина были рас­смотрены в разд. 1. Реологическая схема сплава приведена на рис. 1.36. На рис. 3.33 показаны кривые деформации кристалли­зующегося алюминия А7 под действием постоянной нагрузки. Используя схему, приведенную на рис. 1.36, получим реологические уравнения, описывающие поведение сплавов в интервале кристал­лизации. Эти уравнения впервые были получены Л. П. Кашир­цевым. На схеме последовательно соединены три тела: тело Гука Н₁, тело (S/N₁) и тело Кельвина (H₂/N₂). Поэтому суммарная де­формация всего тела у равна сумме деформаций этих трех тел, т. е.

g = g₁ + g₂ + g₃

С другой стороны, используя реологические законы указан­ных тел, полученные в разд. 2, можно записать следующие урав­нения для напряжений:

t = g₁G₁ (3.14)

t =g₃G₂ + h₂g₃ (3.15)

Для тела (S/N₁) запишем

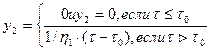
Приведенные уравнения полностью описывают реологическое поведение сплава. Однако, для того чтобы замкнуть эту систему уравнений, необходимо для каждого сплава знать величину предельного напряжения сдвига то, модуля упругости при сдвиге G, модуля G₂, пластической вязкости h₁ и псевдовязкости Кельви­на h₂ как функции температуры. По данным Л. П. Каширцева, все указанные величины в интервале кристаллизации по мере приближения к температуре солидуса резко возрастают. Пример температурных зависимостей реологических характеристик для сплава алюминия с 0,6 % Si приведен на рис. 3.34.

Из системы уравнений (3.14) — (3.15) следует, что деформация сплава является суммой упругой деформации g₁ пластической остаточной деформации g₂ и деформации упругого последействия (обратимой пластической деформации) g₃. Для того чтобы опре­делить, какая из этих видов деформаций влияет на деформацион­ную способность сплава, выполним, следуя Л. П. Каширцеву, от­носительное сравнение их величин.

Уравнения (3.14) — (3.17) позволяют при заданном значении напряжения t определить развитие как суммарной деформации сплава, так и отдельных ее составляющих, если известны реоло­гические характеристики сплава при данной температуре.

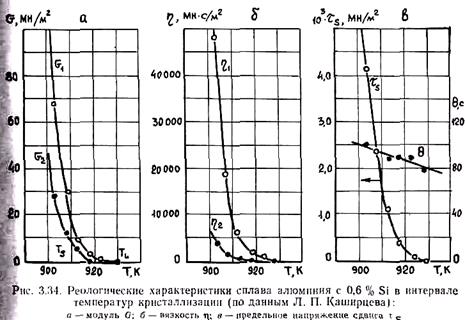
При анализе деформационной способности сплавов чаще всего образцы сплава при данной температуре внутри интервала кри­сталлизации подвергают механическим испытаниям при постоян­ной скорости деформации.

Пусть сплав испытывается при постоянной скорости деформа­ции g = VД = const. Преобразуем исходную систему уравнений:

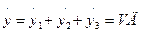
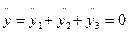
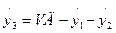
Подставив в это выражение приведенные выше выражения для g₃ и g₃ получим следующие дифференциальные уравнения:

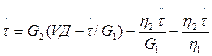
Найдем зависимость т от времени при t < Т₀. Преобразуем со­ответствующее уравнение:

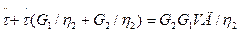
Очевидно следующее начальное условие: при t = 0 t = 0. Най­дем значение t при t = 0. Так как t = 0, то g₃G₂ + h₂g₃ = 0. При t = 0 g₃ = 0, поэтому, как следует из последнего выражения, g₃ = 0, g = g₁ + g₃ = g₁ = VД. Поэтому t = VД×G₁.

Решив это уравнение при данных начальных условиях, получаем формулу

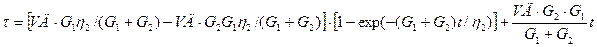
Как показали расчеты с использованием значений реологиче­ских характеристик алюминиевых сплавов, полученных Л. П. Каширцевым, (G₁ + G₂)/h₂ << 1. Поэтому, разлагая экспоненту в ряд с точностью до второго члена, получаем

exp(-(G₁ + G₂)t/h₂) » 1 – (G1 + G2) t/h₂

С учетом этого получаем упрощенное выражение t = VД×G₁×t которое позволяет сделать вывод, что деформацией упругого последействия можно пренебречь в первом приближении. Время, в течение которого напряжение достигает значения предельного напряжения сдвига t₀, равно t₀ = r₀/(VД×G₁).

Решим уравнение для t > 0. Преобразуем его к виду

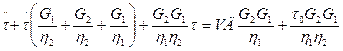
Сформулируем начальные условия: при t = t₀ t = t₀, t = t(t = t₀). Определим t(t = t₀). Так как при t = t₀ g₂ = 0, g₃ = 0 (пренебрегаем развитием упругого последействия при t £ t), то g = g₁ = VД. Поэтому t (t = t₀) = VД × G₁.

Решая дифференциальное уравнение при данных начальных ус­ловиях, получаем

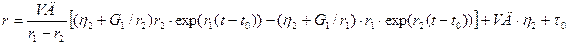
где

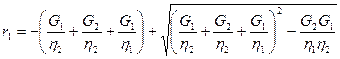
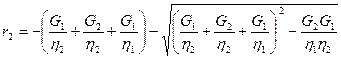
Так как (G₁/h₂ + G₂/h₂ + G₁/h₁) << 1, то, приняв exp(r₁(t - t₀)) » 1 + r₁(t – t₀) и exp(r₂(t – t₀)) » 1 + r₂(t – t₀), после преобразований получим

t = t₀ + G₁VД × (t - t₀)

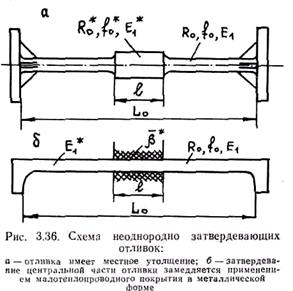
Из этого выражения вытекает, что если r₁(t – t₀) << 1, то пла­стической деформацией и деформацией упругого последействия можно пренебречь по сравнению с упругой. Для того чтобы ре­шить вопрос строго, необходимо из полученной точной формулы найти время, за которое напряжение t достигнет предела проч­ности сплава t_пр, вычислить все виды деформаций, накопленные к этому моменту времени, и сравнить их. Подобные расчеты с применением численных методов на ЭВМ выполнены Л. П. Каширцевым для случая испытания образцов из большого числа алюминиевых сплавов на растяжение. На рис. 3.35 приведены расчетные кривые изменения предельной деформационной способ­ности сплава алюминия с 0,6%Si в интервале его кристаллиза­ции при скорости деформации e=0,00015 с^-1.

Видно, что пластическая деформация e₃ и деформация упру­гого последействия e₂ более чем на порядок меньше упругой деформации e₁. Поэтому приближенно можно принять, что деформа­ционную способность сплавов в интервале кристаллизации необ­ходимо оценивать не по пластической, а по упругой деформации, т. е. e₀ » e₁. Фактическим подтверждением этого вывода является то, что разрушение сплава при образовании горячих трещин носит хрупкий характер.

Вывод о том, что пластическая деформация вблизи темпера­туры солидуса мала, следует из полученной выше формулы Н. Н. Прохорова, из которой видно, что при температуре

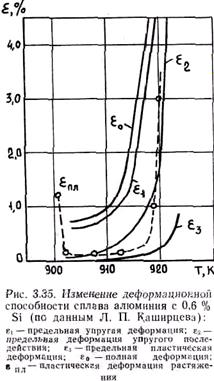
солиду­са пластическая деформация равна нулю. Сравнение деформаци­онной способности сплавов e₀ с относительной свободной усадкой e_у (см. рис. 3.35) показывает, что e_у < e₀. Поэтому величина Δ = min e₀ – mах e_у всегда положительна. Отсюда можно сделать вывод, что даже при полном затруднении горячие трещины не должны образовываться, что противоречит действительности. Сле­довательно, причины образования горячих трещин нужно искать в другом направлении.

3.4.1.3. МЕХАНИЗМ ОБРАЗОВАНИЯ ГОРЯЧИХ ТРЕЩИН

Изложенная выше теория рассматривает сплав с однородным температурным полем в объеме отливки. Все реологические харак­теристики во всех точках сплава одинаковы, поэтому весь объем испытывает однородно распределенные деформации. В реальной отливке скорость охлаждения ее отдельных элементов различна.

При этом неоднородно развивается усадка, и реологические свой­ства распределены в отливке существенно неоднородно. Поэтому в отдельных элементах отливки, которые затвердевают медленнее других, могут локализоваться усадочные процессы. Величина усадки e_у при этом сильно возрастает и может превысить деформа­ционную способность e₀, что приведет к образованию горячих трещин.

Поясним это на следующем примере. На рис. 3.36 приведена отливка, содержащая в середине длины утолщение, а также от­ливка, затвердевание центральной части которой замедлено при­менением малотеплопроводного покрытия металлической формы. Примем, что модули упругости Е в утолщенной и теплоизолированнои частях отливок значительно меньше, чем в остальных частях, так как модуль упругости существенно зависит от темпе­ратуры (с увеличением температуры он уменьшается). При этом крайние участки отливки можно считать жесткими. В сечении, разделяющем центральную и периферийную части, действуют на­пряжения s₁ = E₁×Δl₁/(L₀ - l) и s₂ = E₂×Δl₂/l, где Δl₁ — деформация периферийной части; Δl₂ — деформация центральной части. Очевидно, что исходя из условий равновесия s₁ = s₂ или E₁×Δl₁/(L₀ - l) = E₂×Δl₂/l. С другой стороны, сумма деформаций Δl₁ и Δl₂ должна быть равна свободной усадке всей отливки:

∆l₁ + ∆l₂ = a_св×[(L₀ – l)×(T_у – T₁) + l(Т_у – Т₂),

где T₁ и Т₂ — температура периферийных и центральной частей отливки (Т₂ > T₁). Решив совместно оба приведенных уравнения, получим следующее выражение для относительной усадки цент­ральной части:

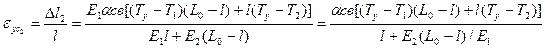
Очевидно, что при E₁ = E₂ и Т₂ = Т₁ e_ус2 = a_св(T_у - Т), т. е. в центральном элементе относительная усадка равна относитель­ной усадке сплава. С уменьшением отношения E₂/E₁ или с уве­личением перепада температур между участками отливки e_ус2 увеличивается и становится больше свободной усадка сплава. Так как модуль упругости по мере приближения к температуре солидуса резко увеличивается, примем E₂ << E₁. При этом

Из этого выражения видно, что, чем больше длина отливки Lo при заданной длине термического узла l, тем больше усадка в этом узле превышает свободную усадку сплава e_ус. На этом ос­новано применение пробы на горячеломкость сплавов А. Татюра (см. рис. 3.29, а). Очевидно, что, чем больше расстояние между утолщениями отливок пробы, тем больше e_ус в них и больше ве­роятность получения горячих трещин.

В общем виде, как предложено Г. Ф. Баландиным, относи­тельную усадку в отдельных частях отливки можно выразить формулой

e = me_у

где m ³ 1 — коэффициент, учитывающий неравномерность охлаж­дения частей отливки.

Горячие трещины возникают, когда при деформации me_у упру­гие напряжения превысят предел прочности сплава, т. е. при Eme_у ³ s_y. Таким образом, горячие трещины образуются чаще всего в термических, толстостенных частях отливки. В данном случае не соблюдается известная истина: где тонко, там и рвется. Для определения коэффициента т необходимо решить тепловую задачу затвердевания сплава (и расчета температурного поля отливки), совмещенную с приведенными выше реологическими уравнениями для расчета деформации сплава и развивающихся напряжений. При этом необходимо использовать экспериментальные данные по реологическим характеристикам сплава в зависи­мости от температуры.

Предел прочности сплава s_в является важнейшим реологиче­ским свойством. С повышением температуры s_в уменьшается.

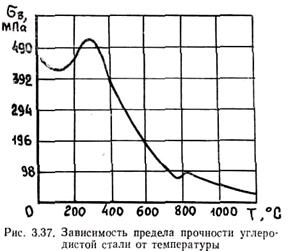
На рис. 3.37 приведен график зависимости s_в углеродистой стали от температуры. Видно, что увеличение температуры до 100 °С приводит к некоторому снижению s_в с последующим его повыше­нием примерно до 300 °С. Дальнейшее увеличение t приводит к рез­кому уменьшению s_в. Зону около 300 °С называют зоной сине­ломкости. При увеличении температуры стали до 1 100°С ее проч­ность уменьшается почти в 10 раз. Систематические и надежные данные по прочности стали в интервале кристаллизации в лите­ратуре отсутствуют. По данным Г. Ф. Баландина, прочность s_в алюминиевых сплавов в интервале кристаллизации изменяется в пределах 0,5 - 1 МПа.

Математическая модель образования горячих трещин для от­ливок простейших конфигураций при некоторых допущениях полу­чена Л. П. Каширцевым. Рассмотрение этой модели и ее реали­зацию на ЭВМ целесообразно осуществить на одном из практи­ческих занятий по курсу.

На основании изложенных выше теоретических положений рас­смотрим важнейшие мероприятия по предотвращению горячих трещин в отливках.

3.4.1.4. МЕРОПРИЯТИЯ ПО БОРЬБЕ С ОБРАЗОВАНИЕМ ГОРЯЧИХ ТРЕЩИН В ОТЛИВКАХ

Все мероприятия могут быть классифицированы по следующим направлениям: конструирование технологических отливок, управ­ление тепловым режимом их затвердевания, повышение податли­вости форм и стержней, повышение жесткости термических узлов отливки, повышение предела прочности сплавов и оптимизация их реологических свойств.

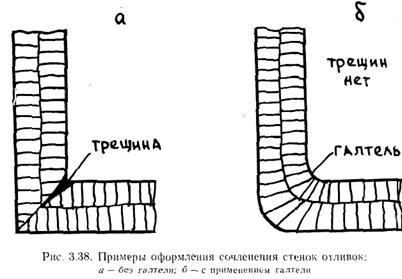
Очевидно, что идеальным было бы конструировать отливки с минимальными перепадами толщин стенок, без термических уз­лов, исключая затруднение усадки. Однако решение максималь­ной задачи нереально. Из изложенной выше теории следует, что нет необходимости устранять термические узлы и торможение усадки. Последнее вообще исключило бы применение металличе­ских форм и стержней. Целесообразно при конструировании от­ливок размещать термические узлы на расстояниях друг от друга L, не превышающих некоторых максимально допустимых значе­ний L_доп. Величину L_доп можно определить по технологическим пробам типа пробы А. Татюра. Если это невозможно из конструк­тивных соображений, то дополнительные тепловые узлы, преду­смотренные с целью уменьшения L, можно удалять последующей механической обработкой. В местах сочленения стенок необходи­мо предусматривать закругления — галтели. На рис. 3.38 приве­дена схема оформления сочленения стенок отливки. Без приме­нения галтелей в месте сочленения часто образуются горячие трещины, так как здесь расположен термический узел и при транскристаллизации в месте стыка столбчатых зон может образовать­ся плоскость слабины.

Более подробно рекомендации по конструированию отливок, а также вопросы улучшения податливости форм и стержней рас­сматриваются в технологических курсах.

Для управления охлаждением затвердевающих отливок приме­няются методы, рассмотренные в гл. 3.3 (внутренние и наружные холодильники, смеси различной теплоаккумулирующей способно­сти и т. п.).

Влияние различных способов управления охлаждением кри­сталлизующейся отливки на прочность стальных образцов с раз­ными термическими узлами показано на рис. 3.39.

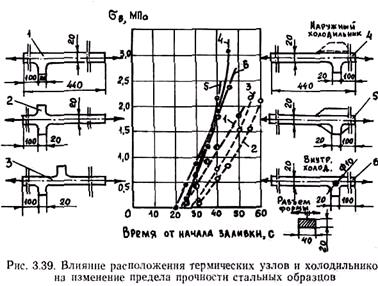
На образование горячих трещин оказывают влияние способ подвода сплава, продолжительность и температура его заливки. Очевидно, что сосредоточенный подвод сплава в термические уз­лы будет способствовать образованию горячих трещин. При этом вероятность их появления будет тем больше, чем выше темпера­тура заливки и больше ее продолжительность. Поэтому подвод сплава целесообразно осуществлять к тонкостенным частям от­ливки. При этом, чем выше температура заливки и медленнее она осуществляется, тем сильнее прогревается форма, оформляющая тонкостенную часть, меньше перепад температур и вероятность образования трещин. Если отливка имеет равномерную толщину стенки, подвод сплава необходимо осуществлять через несколько

распределенных по длине отливки питателей. В отливках простой конфигурации, склонных к образованию усадочных раковин, под­вод сплава целесообразно осуществлять под прибыль, в толсто­стенную часть.

Действенным средством предотвращения горячих трещин яв­ляется выполнение на термических узлах тонкостенных усадочных ребер. Ребра, затвердевая раньше узла, как бы армируют его и, благодаря большей прочности, препятствуют образованию тре­щин (рис. 3.40).

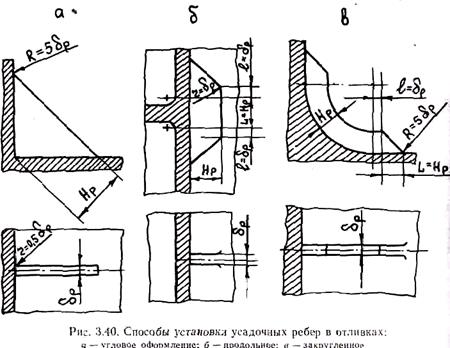
Размеры ребер выбирают по эмпирическим таблицам в зави­симости от толщины основной стенки отливки d₀. В первом при­ближении толщину ребра d_р можно принять равной d₀/3.

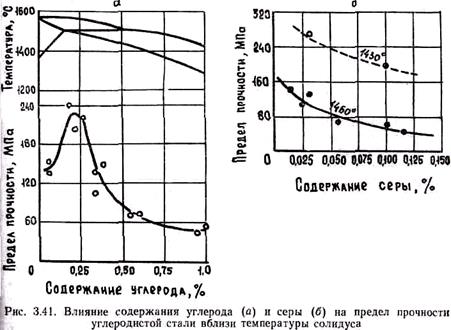
На образование горячих трещин оказывает влияние характер затвердевания сплава. При последовательном затвердевании об­разующаяся твердая корка увеличивает сопротивляемость раз­рушению. Поэтому последовательно затвердевающие сплавы менее склонны к образованию горячих трещин, чем объемно затверде­вающие. Образованию трещин способствуют ликвационные процес­сы, выделение хрупких интерметаллидов и неметаллических вклю­чений. Прочность сплавов в интервале кристаллизации существенно зависит от химического состава сплава (рис. 3.41). Видно, что даже сотые доли процента серы резко снижают прочность стали. Пониженной прочностью, а значит, и склонностью к горя­чим трещинам обладают как низкоуглеродистые (0,2% С), так и высокоуглеродистые стали.

Вопросы горячеломкости различных сплавов и методы воз­действия на нее рассматриваются в технологических курсах.

3.4.2. ЛИТЕЙНЫЕ НАПРЯЖЕНИЯ В ОТЛИВКАХ

После затвердевания отливки осуществляется ее охлаждение в форме, сопровождающееся фазовыми превращениями (напри­ мер превращением a ® g в железоуглеродистых сплавах, выде­лением избыточных фаз по линиям переменной растворимости в алюминиевых, магниевых и других сплавах) и дальнейшим развитием линейной усадки. Тепловая сторона охлаждения отлив­ки рассмотрена в курсе «Основы литейной гидравлики и теплофизики». Развитие линейной усадки и фазовых превращений в твердом состоянии приводит к формированию напряжений в от­ливке. Причиной напряжений является торможение линейной усад­ки и объемных изменений при фазовых превращениях.

Различают механическое и термическое торможение усадки.

Механическое торможение усадки осуществляется стержнями и выступающими частями формы (см. рис. 3.28). Возникающие при этом напряжения называют усадочными. Механическая картина формирования напряжений и деформаций при этом аналогична вышеописанной и принципиально может быть выражена рассмот­ренными уравнениями. Однако температурный интервал здесь гораздо шире интервала образования горячих трещин и охватывает охлаждение отливки от температуры солидуса до комнатной тем­пературы. При этом реологические свойства сплава изменяются в широких пределах. Прежде всего, начиная с температуры соли­дуса, резко увеличивается пластичность сплава, которая при даль­нейшем снижении температуры уменьшается. Суммарная деформа­ция сплава g является суммой упругой и пластической составля­ющих, а также деформации упругого последействия. При этом вблизи температуры солидуса превалирует пластическая дефор­мация и деформация упругого последействия. По мере уменьшения температуры увеличивается влияние упругой деформации, кото­рая является определяющей при низких температурах.

Известно, что пластическая деформация сопровождается де­формационным упрочнением, т. е. приводит к возникновению на­пряжений. Обычно эти напряжения так же, как в законе Гука, считают пропорциональными относительной деформации при зна­чительно меньших значениях коэффициента пропорциональности по сравнению с модулем упругости. При приближенном анализе формирования напряжений, начиная с основополагающих работ русского металлурга Н. В. Калакуцкого, весь температурный интервал разбивают на два участка: высокотемпературный, в ко­тором сплав проявляет только пластические свойства, и низко­температурный, в котором сплав представляет собой чисто упру­гое тело. При этом в пластической области отсутствует деформа­ционное упрочнение, т. е. при деформации не возникает никаких напряжений.

Разделяющую указанные участки температуру перехода из пластической зоны в упругую Т_п принимают равной 0,4¸0,5Т_сол. Для чугуна и стали, по предложению Н. Г. Гиршовича, принима­ют Т_п = 400¸500°'С. Очевидно, что такое представление является идеализированным, так как в зависимости от деформации и на­пряжений во всем интервале температур сосуществуют как пла­стические, так и упругие деформации. Однако, несмотря на это, указанное представление позволяет получить достоверные данные по формированию напряжений как на качественном, так и на количественном уровне. Строгое рассмотрение этого вопроса в на­стоящее время принципиально возможно, но сдерживается отсут­ствием систематических данных о реологических свойствах сплавов во всем интересующем нас температурном интервале.

3.4.2.1. УСАДОЧНЫЕ НАПРЯЖЕНИЯ В ОТЛИВКАХ

Вследствие механического торможения усадки стержнями или выступающими частями формы в отливке возникают растягиваю­щие деформации, равные, как было показано в предыдущем раз­деле, e = e_ус - e_п + e_р. При этом до температуры T = T_п деформа­ции носят пластический характер и напряжения не возникают. При Т < T_п деформации носят упругий характер, что приводит к формированию упругих растягивающих напряжений

s = E[e(T) - e(T_п)] = Ea_св[(T_c – T) – (T_c – T_п)] = Ea_св(T_п – T)