Приняв r » rж, имеем

R_Э = d_Э/2 = 2 см; R_Т.У = d_Т.У× h_Т.У/[2(d_Т.У + h_Т.У)]=12×12/(2×24) = 3 см; m_X/m_Т.У = 0,37(1-2/3) » 0.12

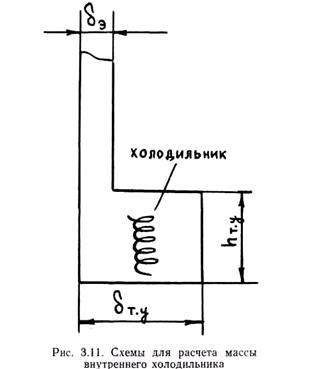
Обычно масса холодильника не превышает 10—15 % от массы захолаживаемого узла отливки. В случае применения спираль­ных холодильников при стальном литье рекомендуют выбирать их массу в пределах 3—4 % от массы питаемого узла. При большей массе холодильники начинают резко ухудшать механические свой­ства стали в захолаживаемом узле. Поэтому если необходимая с точки зрения тепловых условий масса холодильников больше 3—4 %, то их применение следует комбинировать с использова­нием наружных холодильников.

На направленность затвердевания существенное влияние ока­зывают место подвода сплава в форму, температура заливки сплава и скорость заливки. В конечном счете они определяют знак и величину температурного градиента dT/dx по высоте от­ливки. Для усиления направленности затвердевания необходимо, чтобы имел место положительный температурный градиент по высоте отливки (dT/dx > 0). Этому способствует подвод сплава сверху, чаще всего под прибыль. Увеличение продолжительности заливки при подводе сверху увеличивает градиент температур, так как при этом температура в верхних частях отливки и в при­были возрастает. Однако подвод сверху для высоких отливок (H_отл > 300 мм) и отливок, изготовляемых из склонных к окисле­нию и вспениванию сплавов (алюминиевые и магниевые сплавы, высоколегированные стали), применять нельзя из-за возможного разрушения формы, окисления сплава, образования газовой пори­стости и окисных плен в отливках.

При подводе снизу формируется отрицательный температур­ный градиент по высоте отливки, что не способствует направлен­ности затвердевания. При увеличении продолжительности заливки в этом случае охлаждение сплава в форме увеличивается номере его подъема, что приводит к ухудшению условий питания отлив­ки из прибыли. Следует отметить, что при подводе снизу проис­ходит разогрев нижних сечений отливки в процессе заливки фор­мы, особенно в зоне действия питателей. В результате этого около питателей образуются локализованные термические узлы, объем­ная усадка которых не может быть компенсирована перетоком металла из соседних областей отливки, затвердевающих раньше.

Поэтому в зонах около питателей может возникать пористость или концентрированные усадочные раковины. Для их устранения следует применять рассредоточенный подвод сплава через не­сколько питателей, размещенных по периметру отливки. В этом случае количество металла, проходящего через каждый питатель, уменьшается, что снижает перегрев прилегающих к нему обла­стей отливки.

Если отливка толстостенная, то вследствие свободной конвек­ции после заливки формы происходит выравнивание температур по высоте отливки, что уменьшает отрицательное влияние под­вода снизу на направленность затвердевания. Действительно, находящийся после заливки в нижней части полости формы жид­кий сплав имеет меньшую плотность, чем сплав в верхней части формы. В результате возникает конвективный поток, стремящий­ся выровнять температуры в объеме отливки. Однако в относи­тельно тонких отливках для большинства машиностроительных деталей вследствие быстрого увеличения вязкости охлаждающего­ся сплава действие конвекции не проявляется и его можно не учитывать.

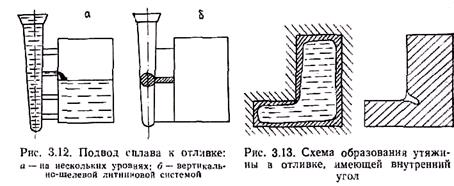
Для высоких отливок и отливок из сплавов, склонных к оки­слению, применяют подвод сплава на нескольких уровнях и че­рез вертикально-щелевые литниковые системы (рис. 3.12). В этих случаях металл подается из стояка через соответствующий пита­тель или щель непосредственно на зеркало поднимающегося в форме сплава, что обеспечивает положительный температурный градиент в отливке. Методы расчета и конструирование таких литниковых систем рассматриваются в курсе «Технология литей­ного производства».

Очень часто в отливках образуются открытые усадочные де­фекты, называемые утяжинами. Они возникают не только на верхних, но и на боковых поверхностях отливки. Рассмотрим механизм образования этих дефектов. Они появляются в тех местах отливки, где по тем или иным причинам скорость нарастания затвердевшей корки замедленна по сравнению с другими участ­ками отливки. Рассмотрим отливку, содержащую внутренний угол (рис. 3.13).

Участок формы, оформляющий внутренний угол отливки, про­гревается более интенсивно (тепло поступает в него через 2 по­верхности), чем остальные поверхности. Поэтому рост твердой корки около него замедлен.

Пусть объем полости формы равен исходному объему жид­кого сплава V₀, плотность жидкого и твердого сплава соответ­ственно rж и rтв, исходная масса жидкого сплава M = V_o×r_mo. К моменту времени t в отливке выделится доля твердой фазы y = m_тв/M. Объем твердой фазы равен V_тв = m_тв/r_тв = My/r_тв. Фактический объем жидкого сплава в этот момент равен V_ж = V₀ – V_тв = M/р_жо - My/r_тв. Плотность жидкого сплава в этот момент будет равна

r_Ж = M_Ж/V_Ж = (M - m_ТВ)/V_Ж = M(1-y)/[1/r_Ж0 - y/r_ТВ] = (1 - y) r_ТВr_Ж0/(r_ТВ - r_Ж0×y = (1 –

- y)r_Ж0/[(r_ТВ - r_Ж0)/r_ТВ + r_Ж0(1 - y)/r_ТВ] = (1 - y)r_Ж0/[e_V + r_Ж0(1 - y)/r_ТВ] = rЖ0/[eV(1 - y) +

+ r_Ж0/r_ТВ] (3.3)

Из этой формулы видно, что с ростом доли затвердевшего сплава y плотность жидкого сплава внутри отливки уменьшается. Известно, что жидкость малосжимаема. Поэтому, в отличие от газов, малейшие изменения плотности приводят к резким измене­ниям давления жидкости. В процессе затвердевания жидкость испытывает деформацию всестороннего растяжения, так как вслед­ствие усадки ее удельный объем увеличивается. Снижение плот­ности жидкости (даже очень малое) приводит к резкому паде­нию давления жидкости внутри отливки Р_ж. В результате на затвердевшую корку сплава действует направленный внутрь пере­пад давлений ΔР = Р_а - Р_ж.

Если затвердевшая корка достаточно толстая, то ее деформа­ция незначительна. В этом случае падение давления жидкости рано или поздно приведет к разрыву сплошности жидкого сплава (при достижении предела прочности жидкости на разрыв) и обра­зованию усадочной раковины. Разрыв сплошности жидкого спла­ва облегчается наличием в нем растворенных газов. Можно при­нять, что образование усадочной раковины произойдет в момент, когда давление в жидкости будет ниже значения, при котором количество растворенных в сплаве газов превысит их раствори­мость, т. е. при Р_ж < [Г]/К², где [Г] — содержание газа, напри­мер водорода, в жидком сплаве, см³/100 г сплава; К — коэффи­циент в законе Сивертса.

В тех местах, где корка тонкая, например в области внутрен­него угла (см. рис. 3.13), перепад давлений вдавливает корку внутрь и образуется утяжина. Очень часто при этом корка проры­вается и в отливке возникает усадочная раковина.

3.3.3. УСАДОЧНАЯ ПОРИСТОСТЬ В ОТЛИВКАХ

Суммарная объемная усадка проявляет себя не только в виде усадочных раковин, но и в виде усадочной пористости. Выше было показано, что даже при чисто последовательном затвердевании в осевых зонах отливки возникает уса­дочная пористость. В отливках всегда имеет место пористость, более или менее неравномерно распределенная по объему отливки. Общий объем уса­дочных дефектов складывается из объема концентрированных раковин и суммарного объема рассредоточенной по отливке пористости, т. е. V_y.д = V_y.p + V_пop. В отливках, затвердев­ших преимущественно последователь­но, превалируют усадочные ракови­ны. При преимущественно объемном затвердевании основным видом уса­дочных дефектов является усадочная пористость. Известна связь характера усадочных дефектов с диаграммой со­стояния сплава (рис. 3.14).

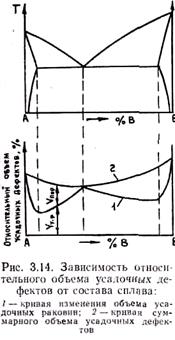
Видно, что минимальный суммар­ный объем усадочных дефектов, как правило, имеют сплавы эвтектическо­го состава. С увеличением ширины интервала затвердевания, т. е. ширины жидкотвердой зоны в отливке и доли объемного затвердева­ния, увеличивается доля усадочных дефектов в виде усадочных пор и уменьшается доля дефектов в виде усадочных раковин. В сплавах эвтектического состава, углеродистых сталях и чистых металлах усадочные дефекты проявляются главным образом в виде усадочных раковин. При литье объемно затвердевающих алюминиевых и магниевых сплавов объем концентрированных раковин очень мал и основным видом дефектов является усадоч­ная пористость.

Рассмотрим механизм образования усадочной пористости, пред­ложенный М. Флемингсом. В условиях объемной кристаллизации в изолированных объемах жидкого сплава между кристаллитами или в междендритных областях происходит уменьшение плотно­сти сплава, и снижение его давления аналогично рассмотренному выше случаю для сплава внутри затвердевающей отливки. Если эти объемы изолированы, т. е. не связаны с соседними, то про­цессы компенсации усадки за счет переноса жидкого сплава от­сутствуют. В этом случае образуются поры за счет разрыва сплош­ности жидкого сплава.

Если же в жидкотвердой зоне имеются междендритные или межзеренные капилляры, то под действием перепада давлений происходит фильтрационный перенос жидкости через капилляры из прибыли или из областей отливки, имеющих запас жидкого сплава. Процесс компенсации усадки за счет направленного массопереноса жидкого сплава называется питанием отливки, а объ­ем жидкого сплава, необходимый для компенсации усадки, назы­вается дефицитом питания. Питание отливки за счет фильтрации жидкости через междендритные и межзеренные капилляры назы­вается фильтрационным питанием. Перепад давлений при фильтрационном питании создается за счет действия внешнего, гидро­статического и отрицательного (меньше атмосферного) давления в объемах жидкости при ее кристаллизации. Процесс уменьшения давления жидкости при ее кристаллизации описан выше (п.3.3.2). Капиллярные силы, если не произошло разрыва сплошности жид­кости, при наличии запаса жидкого сплава в прибыли отсут­ствуют.

где v — вектор скорости фильтрации, отнесенной ко всему попе­речному сечению пористой среды; m — динамический коэффициент вязкости сплава; k—коэффициент проницаемости среды, м²; 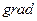P — градиент давления.

Для одномерной фильтрации уравнение Дарси имеет вид

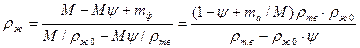
Величину m_ф следует выбрать такой, чтобы в ходе всего про­цесса соблюдалось условие r_ж = r_жo Сократив r_ж и r_жo получаем

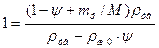; r_ТВ - r_Ж0 × y = r_ТВ - r_ТВ × y + m_Фr_ТВ/M

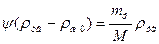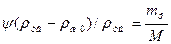; ; e_Vy = m_Ф/M

Массовый поток жидкости в объем V = M/r_жо через ограничи­вающую его поверхность S в единицу времени равен, как извест­но из теории поля,

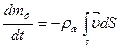
где v — вектор скорости как функция координат точек поверхности. Продифференцируем полученное выше уравнение по времени:

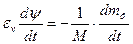
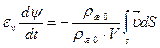
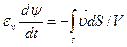
Как известно из теории поля, 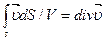— дивергенция вектора скорости. В итоге получаем уравнение неразрывности

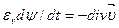(3.6)

Так как 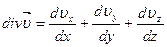, где v_x, v_y, v_z — проекции скорости на соответствующие оси, то

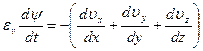(3.7)

Если это условие не выполняется, т. е. фильтрация недоста­точна для полной компенсации усадки, то плотность жидкости будет уменьшаться.

Однако в силу резкого уменьшения давления жидкости при малейшем уменьшении ее плотности изменением плотности мож­но пренебречь вплоть до разрыва сплошности жидкости и обра­зования поры. Поэтому полученное выше уравнение неразрывно­сти, выведенное впервые Г. Ф. Баландиным, можно применять для описания любого режима фильтрации.

Математическая модель фильтрационного питания отливки должна включать в себя краевую задачу затвердевания отливки, позволяющую определить долю твердой фазы y как функцию времени и координат, уравнение Дарси и уравнение непрерывно­сти. Кроме того, должна быть задана функция, связывающая долю твердой фазы y с температурой в интервале ликвидус — солидус. Эксперименты показывают, что эту зависимость можно аппроксимировать формулой

y = A(T_ЛИКВ - T)/(T_СОЛ - В)

где А и В — эмпирические коэффициенты.

Условие образования поры можно записать так: пора обра­зуется, если давление в фильтрационном потоке в данной точке будет меньше величины Pt;p=^[ti]²/kp, где [Н]—содержание водорода в сплаве, т. е. Р а^ Рцр. Величина пористости в жидко-твердой зоне равна

П = V_ПОР/V_З × 100% = e_V(1 - y_КР) × 100%

где y_кр — доля твердой фазы, при которой выполнено указанное условие. Данное значение пористости отнесено к жидкотвердой зоне. Если пористость отнести ко всей отливке, то она равна

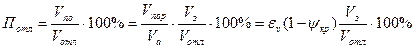
где V_з/V_отл — отношение объема жидкотвердой зоны в момент образования пористости к объему отливки.

В первом приближении коэффициент проницаемости двухфаз­ной зоны отливки можно выразить формулой

k = d²(1 - y)³(150y²)

где d — эффективный диаметр кристаллита. Так как с увеличе­нием доли твердой фазы y k убывает, то в процессе затвердева­ния фильтрационный поток, естественно, уменьшается. В ходе затвердевания эффективный диаметр кристаллита увеличивает­ся. С некоторым приближением, считая кристаллиты сферически­ми, при заданном их числе в единице объема N_V можно полу­чить формулу для вычисления d. Число кристаллитов в двух­фазной зоне (ее ширина определяется в момент снятия перегрева в центре отливки) равно N_k = N_V×N_з. Считая, что все они зародились в один момент времени, можно записать уравнение

r_ТВpd³/6 = yV^Зr_Ж-Т/N_k