Согласно-параллельное соединение звеньев
Это такое соединение, когда на вход всех звеньев подаётся один и тот же сигнал, а выходная переменная равна сумме выходных переменных звеньев (рисунок 3.2).
Если параллельно соединяются n звеньев, то входная величина
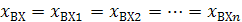 , (3.8)
, (3.8)
а выходная величина
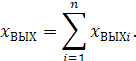
(3.9)
Переходя к изображениям, для передаточной функции согласно-параллельного соединения звеньев получим
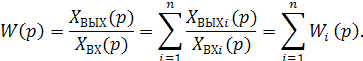
(3.10)
Соответственно переходная функция
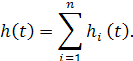
(3.11)
Схема согласно-параллельного соединения n звеньев показана на
рисунке 3.2.
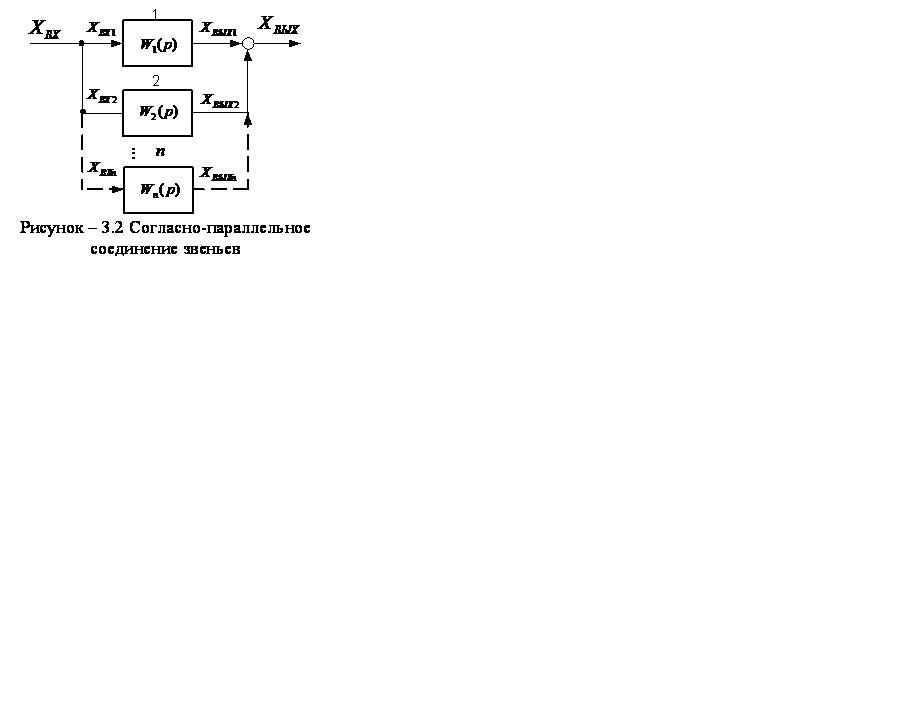
При согласно-параллельном соединении звеньев передаточные, переходные функции складываются.
При согласно-параллельном соединении устойчивых звеньев результирующее звено также будет устойчивым. Это вытекает из того, что общий знаменатель суммы дробей не может иметь иных корней, кроме корней слагаемых, и, следовательно, отсутствие полюсов слагаемых в правой полуплоскости исключает возможность появления таковых в сумме.
Иначе обстоит дело с условием минимальной фазы. Сумма минимально-фазовых передаточных функций может иметь нули в правой полуплоскости и, следовательно, согласно-параллельное соединение ряда минимально-фазовых звеньев может дать неминимально-фазовую систему. Наоборот, при согласно-параллельном соединении неминимально-фазовых устойчивых звеньев может получиться минимально-фазовая устойчивая система.
Переходя к АФЧХ и подставляя вместо р=jω, получим 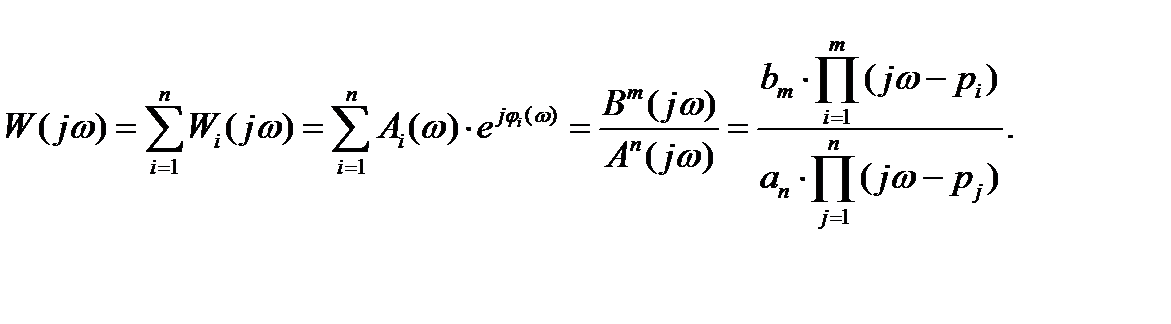 (3.12)
(3.12)
Пусть система составлена из двух звеньев
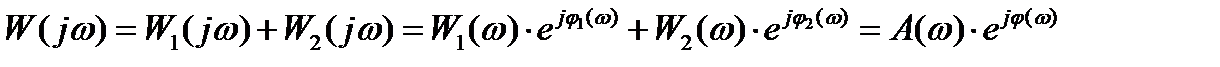 . (3.13)
. (3.13)
Рассмотрим два случая.
1-й случай:
Допустим, что в некотором диапазоне частот A1(ω)> A2(ω), т. е. 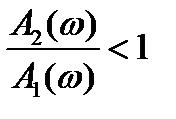 .
.
В этом случае выражение (3.13) удобно преобразовать к следующему виду:
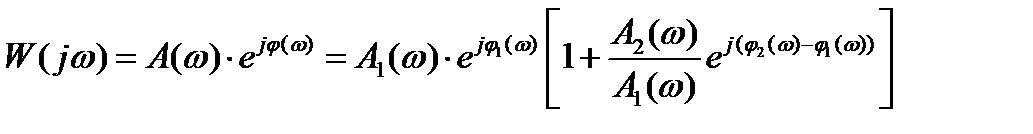 , (3.14)
, (3.14)
Обозначим 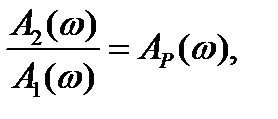
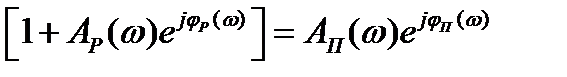 ,
,
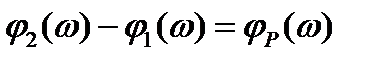 ,
,
тогда 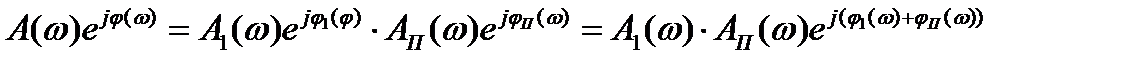 .(3.15)
.(3.15)
Переходя к логарифмическому масштабу, получим:
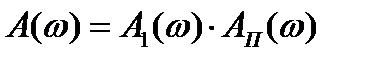
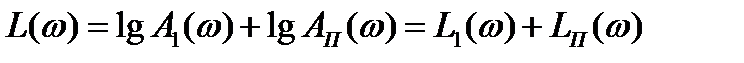 , (3.16)
, (3.16)
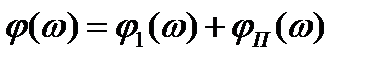 .(3.17)
.(3.17)
Из выражений (3.16), (3.17) следует, что искомые ЛАЧХ и ФЧХ находятся путем добавления поправочных ординат к характеристикам первого звена, т.е. к характеристикам звена ЛАЧХ, которого идет выше.
2-й случай:
Допустим, что в некотором диапазоне частот A2(ω)> A1(ω), т.е. 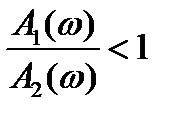 .
.
Тогда преобразуем (3.13) к виду:
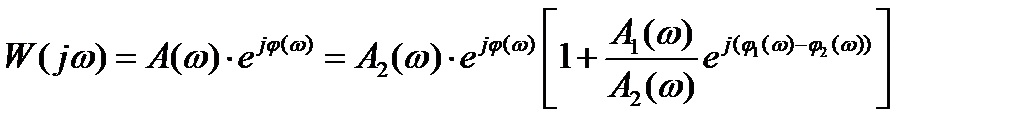 . (3.18)
. (3.18)
Обозначим
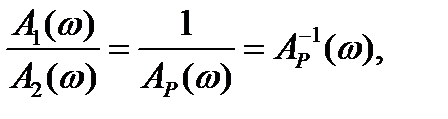
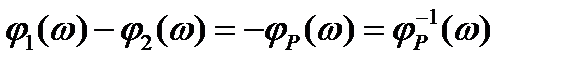 ,
, 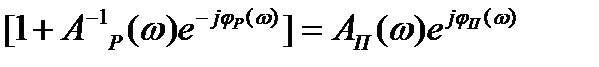 ,
,
имеем
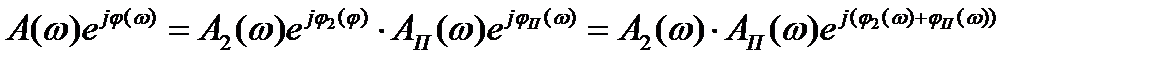 . (3.19)
. (3.19)
Переходя к логарифмическому масштабу, получим:
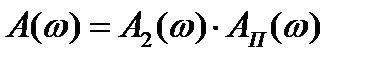
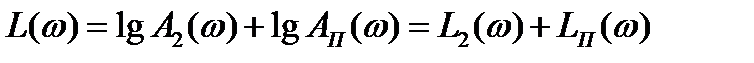 , (3.20)
, (3.20)
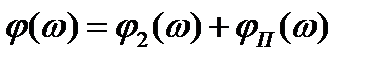 .(3.21)
.(3.21)
Из выражения (3.20), (3.21) следует, что искомые ЛАЧХ и ФЧХ находятся путем добавления поправочных ординат к характеристикам 2-го звена, т.е., опять-таки, к характеристикам звена ЛАЧХ, которого идет выше.
При малых LП (ω) , φП(ω) искомые характеристики будут, очевидно, совпадать с характеристиками того звена ЛАЧХ, которого проходит выше.
Таким образом, основная трудность в построении характеристик согласно-параллельно соединённых звеньев состоит в определении поправок по амплитуде и по фазе.
Эти поправки могут быть найдены из следующих геометрических построений:
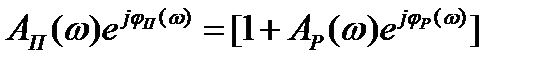 . (3.22)
. (3.22)
Вектор (3.22) представляет собой сумму двух векторов: единичного и вектора AР(jω)
В 1 случае 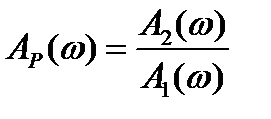 ,
, 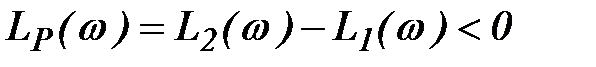 .
.
Во 2 случае 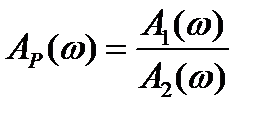 ,
, 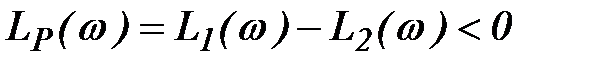 .
.
Порядок определения поправок:
1. Зная L1(ω) и L2(ω) для какой-либо фиксированной частоты находим LР(ω), φР(ω).
2. Переходя к AР(ω), геометрически определяем поправку 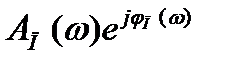 .
.
Рисунок – 3.3 Определение поправок АП(ω) и φП(ω)
Таким образом, суммарная ЛАЧХ при согласно-параллельном соединении звеньев идёт по ЛАЧХ того звена, ЛАЧХ которого лежит выше; суммарная ЛФЧХ идёт по ЛФЧХ того звена, ЛАЧХ которого лежит выше с учётом поправок.
3.3 Понятие об обратных частотных характеристиках
Если есть звено с передаточной функцией W(p) и соответственно переходной функцией 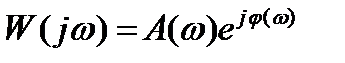 ,то звено, у которого ЛАЧХ и ЛФЧХ обратные, имеет характеристики
,то звено, у которого ЛАЧХ и ЛФЧХ обратные, имеет характеристики
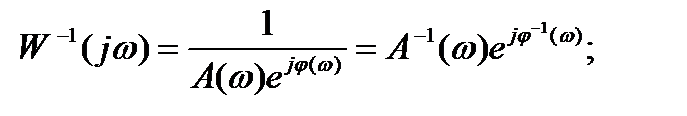 (3.23)
(3.23)
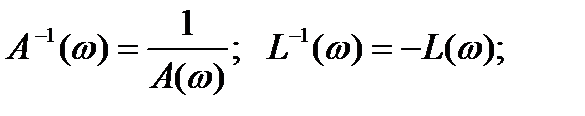
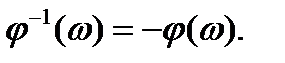
Обратные ЛАЧХ и ЛФЧХ являются зеркальными отображениями прямых ЛАЧХ и ЛФЧХ относительно оси абсцисс.
Дата добавления: 2014-12-22; просмотров: 1099;
