Виды типовых динамических звеньев
Расчетно- проектировочные курсовые и лабораторные задания
для самостоятельной работы студентов
специальностей БТ, ХТВМС, ООС
Составитель: В.В.Гараников,
Редактор
Технический редактор
Подписано к печати
Формат 60х84/16 Бумага писчая
Физ. печ. л. Усл. печ. Уч.-изд.
Тираж . Заказ № Цена
Тверь. Издательство ТГТУ
© Тверской государственный
технический университет,2008.
Типовые динамические звенья
Методические указания к лабораторной работе по дисциплине
"Информационная теория управления" для студентов
направления подготовки бакалавров 230400.62
"Информационные системы и технологии"
профиль "Информационные системы и технологии"
Составитель Г. А. Алексеева
И. В. Чичерин
Утверждены на заседании кафедры
Протокол № от
Рекомендованы к печати
учебно-методической комиссией
направления подготовки бакалавров 230400.62
Протокол № от
Электронная копия находится
в библиотеке главного корпуса
ГУ КузГТУ
Кемерово 2012
ЦЕЛЬ РАБОТЫ
Цель работы – изучение типовых динамических звеньев, их временных и частотных характеристик и приобретение практических навыков по получению характеристик типовых динамических звеньев и исследованию влияния их параметров на вид характеристик.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Виды типовых динамических звеньев
При решении задач анализа и синтеза систем автоматического управления (САУ) широко используется операторный метод [1], базирующийся на преобразовании Лапласа. Это позволяет представить САУ с точки зрения происходящих в них переходных (динамических) процессов как совокупность взаимодействующих между собой динамических звеньев.
Динамическое звено – это математическая модель элемента системы (или части сложного элемента), которая отображает лишь его динамические свойства, а не физическую сущность, происходящих в нем процессов. У каждого динамического звена могут быть только одна входная и одна выходная переменные. Поэтому многомерные элементы системы, то есть элементы с несколькими входными и выходными переменными разделяют на соответствующее число динамических звеньев. Основным свойством динамического звена является свойство однонаправленности, то есть выходная переменная динамического звена не оказывает на него какого-либо влияния.
Элементы САУ различные по физической природе, конструктивному исполнению, принципу действия и другим характеристикам, но описываемые линейными дифференциальными уравнениями одного и того же вида имеют одинаковые передаточные функции, то есть являются одинаковыми (однотипными) динамическими звеньями.
Для облегчения (упрощения) решения задач анализа и синтеза САУ сложные динамические звенья разбиваются на более простые, так называемые типовые динамические звенья (ТДЗ), которые описываются линейными дифференциальными уравнениями не выше второго порядка. ТДЗ могут быть как составными частями звеньев САУ, так и самостоятельными звеньями системы, поэтому знание их характеристик существенно облегчает анализ и синтез таких систем.
ТДЗ, в общем случае [2, 3], описываются линейным дифференциальным уравнением второго порядка вида:
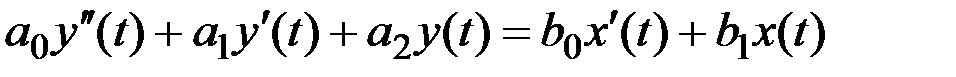 , (2.1)
, (2.1)
или соответствующей передаточной функцией
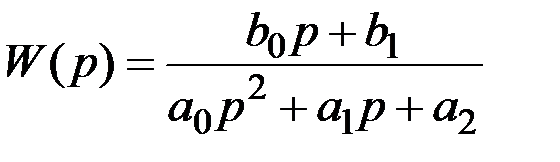 , (2.2)
, (2.2)
где a0, а1, а2, b0, b1 – постоянные коэффициенты дифференциального уравнения (параметры передаточной функции);
x(t), y(t) – соответственно, входная и выходная переменные ТДЗ;
t – непрерывное время;
p – оператор дифференцирования 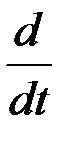 .
.
При обращении в нуль тех или иных коэффициентов дифференциального уравнения (2.1) изменяется как вид дифференциального уравнения, так и вид передаточной функции (2.2), что отражает изменение динамических свойств звена. Если а2≠0 и b1≠0, то ТДЗ обладают статизмом, то есть однозначной связью между выходной и входной переменными в установившемся режиме. ТДЗ, у которых а2≠0, а1≠0, а0≠0, обладают инерционностью.
Перечень ТДЗ, их условные обозначения и значения коэффициентов приведены в таблице 2.1, где k – коэффициент передачи звена; Т, Т1, Т2 – постоянные времени; ξ – коэффициент демпфирования (затухания). Так как в настоящее время нет установившегося мнения о количестве и перечне ТДЗ, то в таблице 2.1 приведены только те звенья, которые наиболее часто встречаются в литературе.
Пользуясь таблицей 2.1, можно без труда записать дифференциальное уравнение и передаточную функцию для любого ТДЗ. В качестве примера рассмотрим колебательное и реальное дифференцирующие звенья.
Колебательное звено имеет следующие значения коэффициентов:
а0=Т 2; а1=Т1=2ξТ; а2=1; b0=0; b1=k.
Тогда в соответствии с выражениями (2.1) и (2.2) можно записать
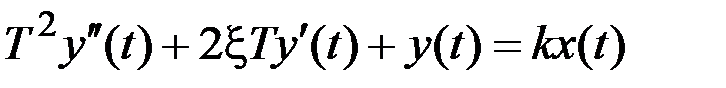 , (2.3)
, (2.3)
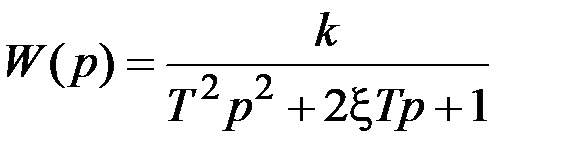 . (2.4)
. (2.4)
Таблица 2.1 – Типовые динамические звенья и коэффициенты
их дифференциальных уравнений
| № | Ус-ловное обозначение | Наименование звена | а0 | а1 | а2 | b0 | b1 | Примечание |
| УЗ | Безинерционное (усилительное, пропорциональное) | k | ||||||
| АЗI | Апериодическое (инерционное) первого порядка | Т | k | |||||
| АЗII | Апериодическое второго порядка | Т22 | Т1 | k | Т1 ≥ 2Т2 | |||
| КБЗ | Колебательное | Т2 | Т1 | k | Т1=2ξТ; 0<ξ<1 | |||
| КНЗ | Консервативное (идеальное колебательное) | Т2 | k |
Продолжение таблицы 2.1
| № | Ус-ловное обозначение | Наименование звена | а0 | а1 | а2 | b0 | b1 | Примечание |
| ИИЗ | Идеальное интегрирующее | k | ||||||
| РИЗ | Реальное интегрирующее | Т | k | |||||
| ИЗ | Изодромное (пропорционально-интегрирующее) | k1 | k | k1=kТ | ||||
| ИДЗ | Идеальное дифференцирующее | k | ||||||
| РДЗ | Реальное дифференцирующее | Т | k | |||||
| ФЗ | Форсирующее | k1 | k | k1=kТ |
Реальное дифференцирующее звено имеет следующие значения коэффициентов:
а0=0; а1=Т; а2=1; b0=k; b1=0.
Тогда можно записать:
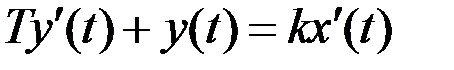 ; (2.5)
; (2.5)
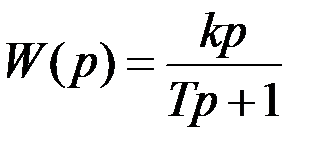 . (2.6)
. (2.6)
Типовые динамические звенья, приведенные в таблице 2.1, делятся на три класса:
– позиционные звенья (усилительное, апериодическое первого и второго порядков, колебательное, консервативное);
– интегрирующие звенья (идеальное и реальное интегрирующие, изодромное);
– дифференцирующие звенья (идеальное и реальное дифференцирующие, форсирующее).
Позиционные звенья (кроме консервативного) характеризуются тем, что в каждом из них при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной переменной. Отношение установившегося значения выходной величины к входной величине определяется коэффициентом передачи k. Наличие и продолжительность переходного процесса определяется постоянной времени Т (чем больше Т, тем больше длится переходный процесс). Особенность консервативного звена состоит в том, что оно характеризуется незатухающими колебаниями на выходе при постоянном воздействии на входе.
Интегрирующие звенья характеризуются тем, что при постоянном входном воздействии выходная переменная y(t) неограниченно возрастает. В этих звеньях коэффициент передачи k характеризует скорость этого роста.
Дифференцирующие звенья реагируют только на изменение входной переменной. Форсирующее звено сочетает в себе свойства позиционных и дифференцирующих звеньев.
Важное место среди ТДЗ занимает звено чистого запаздывания. Это звено передаёт входное воздействие с входа на выход без искажения формы. Однако все мгновенные значения входного воздействия выходная переменная принимает с некоторым отставанием (запаздыванием).
Звено чистого запаздывания (ЗЧЗ) описывается уравнением
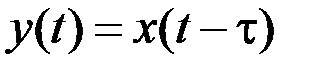 , (2.7)
, (2.7)
где τ – время запаздывания.
Уравнение (2.7) не является дифференциальным, а относится к классу особых уравнений со смещённым (запаздывающим) аргументом. Передаточная функция звена чистого запаздывания не является дробно-рациональной функцией и определяется следующей формулой:
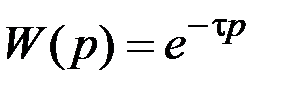 . (2.8)
. (2.8)
ТДЗ можно разделить на звенья, которые поддаются дальнейшему расчленению, и звенья, которые не поддаются дальнейшему расчленению. Последние звенья называются элементарными ТДЗ и к ним относятся: усилительное, апериодическое первого порядка, колебательное (консервативное), идеальное интегрирующее и идеальное дифференцирующее звенья, а также звено чистого запаздывания. Остальные ТДЗ можно получить из элементарных звеньев. Например, апериодическое звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка, реальное интегрирующее звено - как последовательное соединение идеального интегрирующего звена и апериодического звена первого порядка.
2.2 Временные характеристики
типовых динамических звеньев
Временными характеристиками ТДЗ называются графики решения их дифференциальных уравнений при некоторых стандартных (типовых) воздействиях. В качестве стандартных воздействий в основном рассматриваются:
– единичное ступенчатое воздействие (единичная ступенчатая функция) 1(t), то есть:
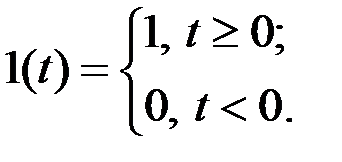 (2.9)
(2.9)
График единичного ступенчатого воздействия представлен на рисунке 2.1.
– единичное импульсное воздействие δ(t):
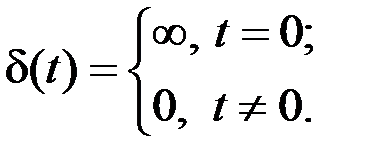 (2.10)
(2.10)
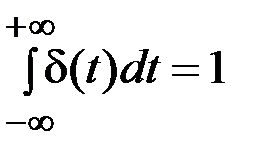 .
.
Воздействие δ(t) представляет собой импульс бесконечно большой амплитуды и бесконечно малой длительности (рис. 2.2).

Рисунок 2.1 – График единичного ступенчатого воздействия

Рисунок 2.2 – График единичного импульсного воздействия
В качестве временных характеристик рассматриваются:
– переходная функция h(t), характеризующая переходный процесс, вызванный единичным ступенчатым воздействием при нулевых начальных условиях;
– весовая (импульсная переходная) функция ω(t), характеризующая переходный процесс, вызванный единичным импульсным воздействием при нулевых начальных условиях.
Временные характеристики ТДЗ приведены в приложении (таблица А.1).
2.3 Частотные характеристики
типовых динамических звеньев
Частотные характеристики описывают переходные свойства ТДЗ в режиме установившихся гармонических колебаний, вызванных внешними гармоническими колебаниями.
Основными частотными характеристиками ТДЗ являются:
– амплитудно-фазовая частотная характеристика (АФЧХ), график частотной передаточной функции:
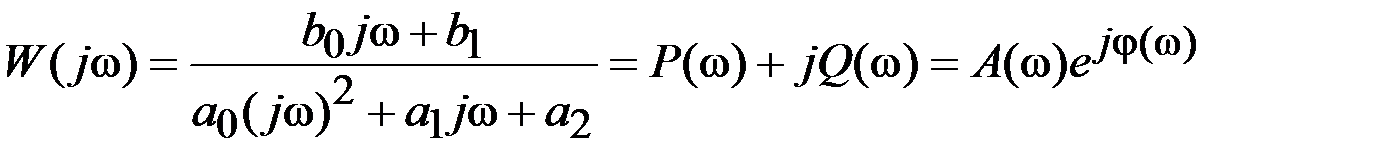 , (2.11)
, (2.11)
где j – мнимая единица;
P(w) – вещественная частотная характеристика;
Q(w) – мнимая частотная характеристика;
A(w) – амплитудная частотная характеристика;
φ(w) – фазовая частотная характеристика;
– вещественная частотная характеристика (ВЧХ) P(ω):
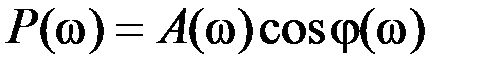 ; (2.12)
; (2.12)
– мнимая частотная характеристика (МЧХ) Q(ω):
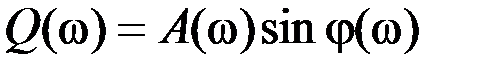 ; (2.13)
; (2.13)
– амплитудная частотная характеристика (АЧХ) А(ω):
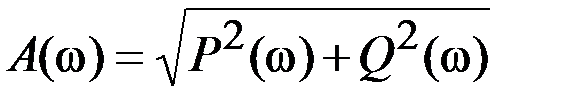 ; (2.14)
; (2.14)
– фазовая частотная характеристика (ФЧХ) φ(ω):
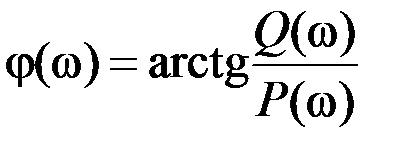 . (2.15)
. (2.15)
При синтезе САУ широко используются логарифмические характеристики:
– логарифмическая амплитудно-частотная характеристика (ЛАЧХ)
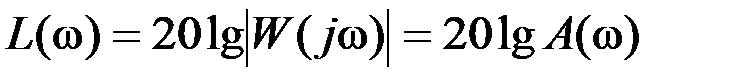 ; (2.16)
; (2.16)
– логарифмическая фазовая частотная характеристика (ЛФЧХ), которая представляет собой фазовую частотную характеристику φ(ω), построенную в логарифмическом масштабе частот.
В приложении (таблица А.2) приведены выражения для нахождения частотных характеристик ТДЗ и графики АФЧХ, ЛАЧХ, ЛФЧХ.
Дата добавления: 2014-12-06; просмотров: 3786;
