Введение в курс Теория телетрафика

Тraffic – означает «поток, движение». Teletraffic можно интерпретировать, как движение сообщений по каналам связи, нагрузку канала или сети каналов с учетом прохождения через ряд физических устройств, обеспечивающих управление потоком сообщений.

Теория телетрафика (ТТ) определена как применение теории вероятностей к решению проблем планирования, оценки производительности, технической эксплуатации и обслуживания телекоммуникационных систем.

Основоположником ТТ является Агнер Краруп Эрланг (1878-1929г.).Предположения, выводы сделанные Эрлангом в его работах, получили дальнейшее развитие в работах Т.Энесета, Г. О^,Делла, К. Пальма, Т. Фрая, А. Хинчина, В. Бенеша, А. Лотце, Г. Башарина, М. Шнепса, А. Харкевича, А. Пшеничникова, Б. Лившица,

Ю. Корнышева, Г. Ионина, С. Степанова и многих других учёных.

Результаты работ этих ученых, как базовые положения теории массового обслуживания, используют при оценке работы сетей связи.

Сеть связи – это совокупность функционально связанных единой целью физических устройств, процессов и задач.

Предметом ТТ является количественная сторона процессов обслуживания потоков сообщений в сетях связи с помощью соответствующих математических моделей. Для компактной записи математических моделей часто используется система обозначений, предложенная Д.Кендаллом-Ли:

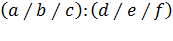, (1.1)

где a– распределение времени между заявками во входном потоке;

b –распределение времени между моментами конца обслуживания в выходном потоке;

c–число параллельно задействованных узлов обслуживания;

d –дисциплина очереди:

ПЕРППО – первый пришел, первый обслужен.

ПОСППО – последний поступил, первый обслужен.

СОЗ – случайный отбор заявок на обслуживание.

e –максимально допустимое число заявок принимаемых системой массового обслуживания;

f-число одиночных источников заявок (клиентов).

Система обозначений (1.1) была модифицирована Г.П. Башариным и имеет следующий вид:

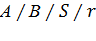, (1.2)

где А – обозначает функцию распределения промежутков между вызовами;

B – обозначает функцию распределения длительности обслуживания;

S – схема обслуживания;

r -дисциплина обслуживания.

Для обозначения типов распределения, чаще всего используются следующие символы: M-показательное, Е-эрланговское, D-равномерной плотности,

G-произвольное.

В ТТ широко используется модель вида: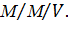

Например, для определения емкости пучка соединительных линий (СЛ) между двумя системами коммутации. Для пучка соединительных линий емкостью V, заявкой будет вызов, поступающий на вход соответствующей системы коммутации

Длительностью обслуживания становится время занятия линий в пучке СЛ. Обслуживающим прибором следует считать набор из V-линий, который образует пучок СЛ.

Обычно пучок СЛ работает, как система массового обслуживания с потерями. Это означает, что при занятости всех V-линий, поступивший вызов теряется. Можно обозначить вероятность потери вызова – . Для данного примера возникает четыре задачи:

1. По известным величинам интенсивности входного потока вызовов и интенсивности обслуживания, необходимо найти такую емкость пучка V, чтобы вероятность потерь не превышала заранее выбранный порог .;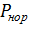

2. По известным величинам интенсивности входного потока вызовов и интенсивности обслуживания, а также с заданной емкостью пучка V,найти вероятность потери вызова .;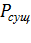

3. По известным величинам интенсивности входного потока вызовов емкости пучка V,допустимой вероятности потерь 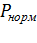, найти допустимую величину интенсивности обслуживания;

4. По известным величинам интенсивности обслуживания, емкости пучка соединительных линий V, и допустимой вероятности потерь вызовов 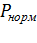, найти допустимую величину интенсивности входного потока вызовов.

Данный пример, одна из важнейших практических задач эффективного развития сетей телефонной связи в начале XXв., ее успешно решил А.К.Эрланг. Формула, которую он вывел, получила название первая формула Эрланга.

Более сложный пример, - цифровой тракт между узлами коммутации мультисервисной сети, по этому тракту передаются пакеты, для обслуживания которых используется дисциплина с ожиданием.

Из очереди пакеты извлекаются с учетом назначенных им приоритетов для обработки и передачи, поэтому к перечисленным выше четырем задачам, представляющих практический интерес, следует добавить решение таких проблем, как:

1. Анализ длительности задержки пакетов в узлах мультисервисной сети;

2. Выбор оптимальных правил назначения приоритетов с учетом факторов характерных для мультисервисной сети.

Таким образом, основная цель ТТ может быть сформулирована следующим образом: с помощью соответствующих математических моделей получить соотношение между качеством обслуживания и пропускной способностью исследуемой системы.

В соответствии с этим задача ТТ состоит в том, чтобы наиболее эффективно проектировать телекоммуникационные системы с учетом заданных количественных характеристик качества обслуживания.

При практическом применение методов ТТ возникает ряд задач, связанных с ближайшими и длительными сроками оценки полученных результатов.

Задачи на ближайшие сроки могут включать: решение задач по определению емкости пучков СЛ, числа операторов соответствующих служб, распределение приоритетов между рабочими местами в компьютерной сети и т.д.

Задачами на перспективу могут быть, например: принятие решений относительно развития телекоммуникационной сети, включающих определения необходимого количества систем передачи, количество определенного кабельного оборудования.

Основными методами решения задач ТТ являются:

1. Аналитические методы;

2. Приближенные методы решения (интеграционные или численные);

3. Методы статистического моделирования.