Оператор Лапласа в сферических координатах распадается на радиальную и угловую части
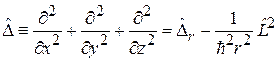 . (4.9)
. (4.9)
Угловая часть содержит квадрат момента импульса 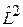 . Радиальная часть оператора Лапласа
. Радиальная часть оператора Лапласа
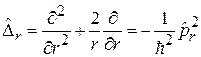 (4.10)
(4.10)
выражается через радиальный импульс
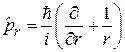 . (4.11)
. (4.11)
Выполняется
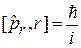 ,
, 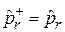 . (4.12)
. (4.12)
Доказательство соотношений (4.10) – (4.12) выносится на практические занятия.
Повышающий и понижающий операторы
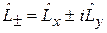 (4.13)
(4.13)
ступенчато изменяют собственные функции и собственные значения оператора 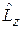 и удовлетворяют соотношениям
и удовлетворяют соотношениям
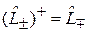 ,
,
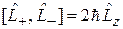 , (4.14)
, (4.14)
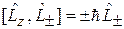 , (4.15)
, (4.15)
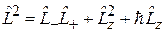 . (4.16)
. (4.16)
Оператор поворота 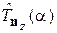 поворачивает углового состояния частицы
поворачивает углового состояния частицы 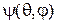 вокруг оси z на угол a
вокруг оси z на угол a
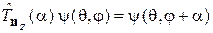 . (4.17)
. (4.17)
Получим выражение оператора, разлагая 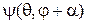 в ряд Тейлора и учитывая (4.7)
в ряд Тейлора и учитывая (4.7) 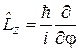
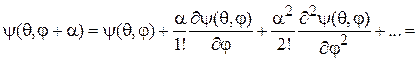 =
= 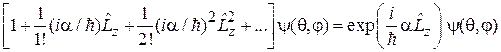 .
.
Сравниваем с (4.17), находим
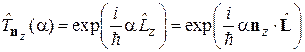 . (4.18)
. (4.18)
где 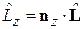 .
.
Обобщаем (4.18) на случай поворота вокруг единичного вектора nна угол a, отсчитываемый по правилу правого винта, получаем
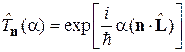 , (4.19)
, (4.19)
где оператор момента импульса является генератором поворота состояния частицы.
Сферическая функция
Сферическая функция 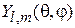 является собственнойфункцией взаимно коммутирующих операторов
является собственнойфункцией взаимно коммутирующих операторов 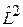 и
и 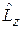
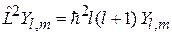 , (4.20)
, (4.20)
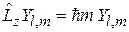 , (4.21)
, (4.21)
где 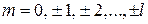 – магнитное квантовое число, определяет проекцию орбитального момента L на ось z
– магнитное квантовое число, определяет проекцию орбитального момента L на ось z
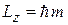 .
.
Дата добавления: 2019-10-16; просмотров: 1336;
