Орбитальное квантовое число определяет модуль орбитального момента L

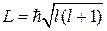. (4.22)

Состояния 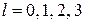обозначаются в спектроскопии буквами s, p, d, f от англ. sharp – резкий, principal – главный, diffuse – расплывчатый, fundamental – фундаментальный.

Количество проекций L на ось z равно числу возможных значений 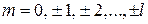, в результате число проекций

.

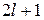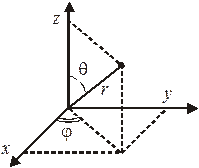
Направление L определяется углом θ с осью z. Угол квантуется

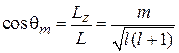. (4.23)

Пространственное квантование при l = 3

Вектор L не может быть направлен вдоль оси z, поскольку максимальная проекция вектора не может превышать его модуль

,

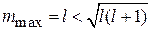тогда из (4.23) находим

, .

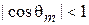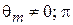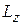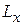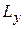Физическая причина в том, что определенность приводит к неопределенностям некоммутирующих с ним и , которые дают вклад в 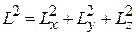, поэтому .

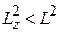Из (4.15)

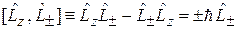
и (4.21)

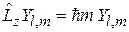
получаем

.

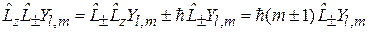Следовательно, операторы 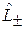переводят состояние с собственным значением m в состояния с собственными значениями 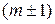, то есть 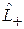повышает у состояния число m на единицу, а 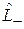понижает на единицу.

Выполняется

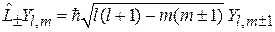, (4.24)

полученное в курсе «Методы математической физики».

Выражение для сферической функции 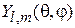. В сферических координатах изменения углов θ и φ происходят независимо, поэтому функция состояния факторизуется

.

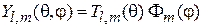В уравнение на собственную функцию (4.21)

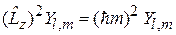
подставляем оператор (4.7)

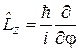
получаем уравнение

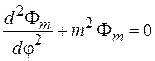. (4.25)

Накладываем условие периодичности

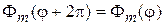. (4.26)

Из (4.25) и (4.26) получаем

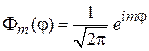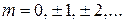, (4.27)

Условие периодичности (4.26) привело к квантованию числа m. На основании

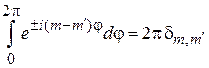
функции 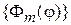, где 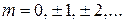, удовлетворяют условию ортонормированности

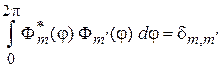. (4.28)

Для оператора квадрата момента импульса (4.8)

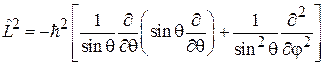
уравнение на собственную функцию (4.20)

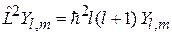
дает дифференциальное уравнение

.

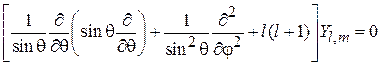Решение в виде

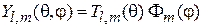
с учетом (4.27)

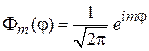
приводит к уравнению для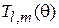

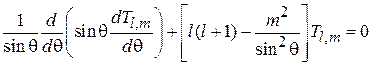. (4.29)

Уравнение совпадает с уравнением для присоединенных функций Лежандра 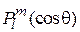, тогда ,

.

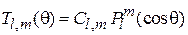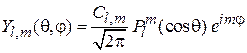Постоянный множитель 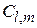определяется из условия нормировки

, .

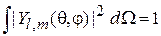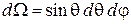В результате

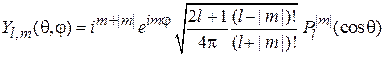. (4.30)

Выполняются

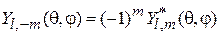, (4.31)

, ,

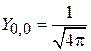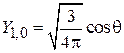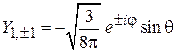, (4.32)

и условие ортонормированности

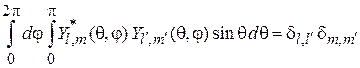. (4.33)

Инверсия координат 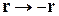соответствует замене

, ,

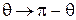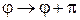тогда

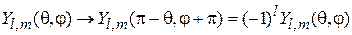. (4.34)

Четность состояния, описываемого сферической функцией, совпадает с четностью орбитального числа l.