Операторы момента импульса

В квантовой механике вращение описывается операторами момента импульса, их собственными функциями и собственными значениями. Основные соотношения рассматривались в курсе «Методы математической физики», поэтому далее дается лишь обзор основных результатов.

Декартовые координаты. По правилу соответствия между классическими и квантовыми соотношениями величины в (4.1) заменяются операторами, тогда оператор момента импульса

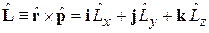, (4.2)

где с учетом

, , ,

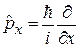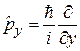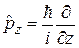операторы декартовых проекций момента импульса

,

;

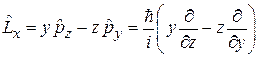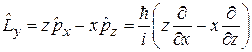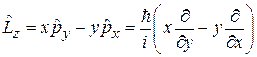, (4.3)

Оператор квадрата момента импульса

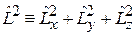. (4.4)

Операторы эрмитовые

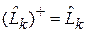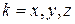, . (4.5)

Доказательство (4.5) выносится на практическое занятие.

Перестановочные соотношения следуют из (4.3) с учетом

, , ,

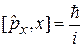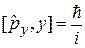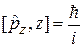И имеют вид

,

,

,

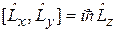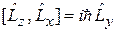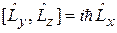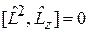. (4.6)

Из 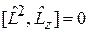следует, что квадрат модуля 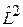и проекция на декартовую ось 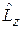измеримы одновременно с неограниченной точностью, наборы их собственных функций совпадают. Собственные значения этих операторов – орбитальное число l и магнитное число m описывают вращательное состояние частицы.

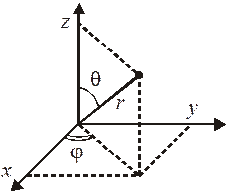
Сферические координаты 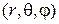связаны с декартовыми координатами .

; ; ,

,

,

,

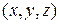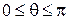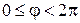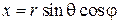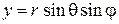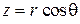Операторы в сферических координатах имеют вид

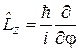, (4.7)

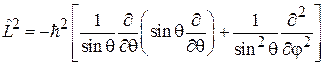. (4.8)