Закон сохранения момента импульса

В механике моментом импульса материальной точки относительно некоторой точки О называется векторная величина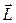

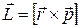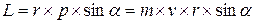; . (3.4)

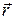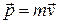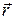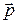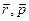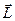Здесь – радиус-вектор, определяющий положение материальной точки относительно точки О, – импульс материальной точки, α – угол между векторами и . Направление вектора момента импульса определяется по правилу правого винта (вектора и составляют правую тройку векторов).

Для системы материальных точек момент импульса равен векторной сумме моментов импульсов отдельных материальных точек системы или векторному произведению радиус-вектора центра масс системы на импульс ее центра масс

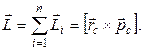(3.5)

При вращательном движении все точки, составляющие тело, движутся по окружности. Момент импульса материальной точки массой m, движущейся равномерно со скоростью v по окружности радиуса R, равен

L=mvRsin90º=mvR. (3.6)

При этом момент импульса твердого тела L=Iω, где I – момент инерции тела, ω – его угловая скорость.

Момент инерции I является мерой инертности тела во вращательном движении. Для системы материальных точек момент инерции равен .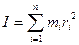

Изотропность пространства (осевая симметрия пространства) приводит к закону сохранения момента импульса: в замкнутых системах момент импульса сохраняется.

В предыдущем параграфе обсуждался вопрос о существовании замкнутых систем. Установлено, что в ряде случаев законом сохранения момента импульса можно пользоваться и для незамкнутых систем. Приведем примеры.

1. Если суммарный момент внешних сил равен нулю, то момент импульса системы сохраняется.

2. Если существует ось Z такая, что сумма проекций моментов внешних сил на эту ось равна нулю, то сохраняется проекция момента импульса системы на эту ось.

3. Момент импульса системы сохраняется, если время действия внешних сил мало.

Закон сохранения момента импульса является фундаментальным законом природы, выполняющимся при любых взаимодействиях в мега-, макро- и микромире. Законом сохранения момента импульса объясняются, в частности, плоская форма галактик, орбитальное движение планет Солнечной системы (второй закон Кеплера), изменение угловой скорости вращения фигуриста при изменении положения его рук и т.д.

Многие элементарные частицы обладают внутренним моментом импульса (спином). Суммарный спин системы взаимодействующих частиц сохраняется при любых процессах слабого и сильного взаимодействий.

Контрольные вопросы

1. Приведите примеры тел, обладающих осью симметрии четвертого порядка. Какой симметрией обладают снежинки?

2. Приведите примеры зеркальной симметрии.

3. Чему равен импульс земного шара при его суточном вращении?

4. Почему пушка откатывается при выстреле, а ружье отдает в плечо?

5. Как объясняется реактивное движение?

6. Каким образом закон сохранения импульса объясняет наблюдаемую форму галактик?

7. Как закон сохранения момента импульса отражается на движении планет Солнечной системы?

8. Как объяснить изменение угловой скорости вращения фигуриста при изменении распределения его массы относительно оси вращения?

9. Сравните нарезное и гладкоствольное оружие по точности и дальности полета.

10. Что такое гироскопы? Где они применяются?

11. Можно ли сконструировать вертолет с одним винтом?

12. Почему акробат, делая сальто-мортале, старается сгруппироваться (сжаться в клубок) ?

13. Какое состояние системы называется устойчивым? Чем оно характеризуется?

14. Почему массивные небесные тела обладают шарообразной формой?

15. Какую роль законы сохранения сыграли в открытии нейтрино и ряда других элементарных частиц?

16. Тело брошено под углом к горизонту. В какой точке траектории тело обладает наименьшей кинетической энергией? Наименьшей потенциальной энергией? Как изменяется полная механическая энергия тела во время полета в отсутствие трения?