Закон сохранения момента импульса

Рассмотрим произвольную систему частиц:

,

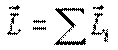(5.7)

где все векторы определены относительно одной и той же точки O выбранной ИСО.

Продифференцируем (5.7) по времени:

,

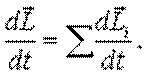
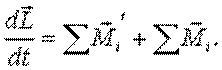
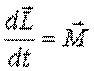(5.8)

где 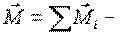суммарный момент всех внешних сил.

Приращение момента импульса системы за конечный промежуток времени

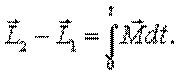
(5.9)

Закон сохранения момента импульса: в инерциальной системе отсчета момент импульса замкнутой системы частиц остается постоянным, т.е, не меняется со временем.

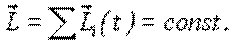
(5.10)

В проекциях на ось:

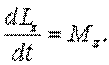
(5.11)

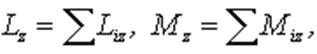
(5.12)

где 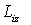и - момент импульса и момент внешних сил относительно оси z для 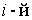частицы (твердого тела) системы.

И ,следовательно,

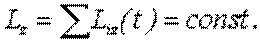
(5.13)

При этом сам вектор 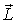, определенный относительно произвольной точки O на этой оси, может меняться.

Центр масс

Центр масс является точкой приложения вектора импульса системы 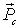, так как вектор любого импульса является полярнымвектором. Положение точки С относительно начала О данной системы отсчета характеризуется радиусом-вектором, определяемым следующей формулой:

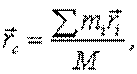
(5.15)

где 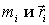- масса и радиус-вектор каждой частицы системы, M - масса всей

системы (рис. 5.3).

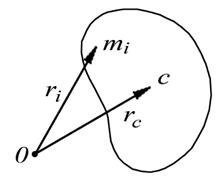
Рис. 5.5. Определение центра масс системы частиц

Центр масс системы совпадает с ее центром тяжести.

При движении любой системы частиц ее центр инерции движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы, действующие на систему. При этом ускорение центра инерции совершенно не зависит от точек приложения внешних сил.