Линейная парная регрессия
Методы и модели регрессионного анализа занимают центральное место в математическом инструментарии эконометрики. Наиболее часто используется парная регрессия, когда рассматривается пара переменных: одна объясняющая (синонимы - входная, экзогенная, регрессор) переменная Х и одна – объясняемая (синонимы - выходная, результирующая) переменная Y – обязательно случайная величина.
Регрессией называют функцию, отражающую зависимость математического ожидания (МО) СВ Y от значений Х (такую зависимость называют также корреляционной). По определению регрессия есть условное МО СВ Y:
| Мх(Y) = j(х). | (2.1) |
На практике точно не известно условное МО СВ Y, т.е. функция j(х). Поэтому можно говорить лишь о приближенном построении - оценке такой функции. Исходными данными для этого служат n пар значений Х и Y: xi и yi при i=1, 2, ... , n.
В случае парной линейной регрессии в качестве оценки - выборочного уравнения регрессии - принимается прямая линия:
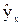 = bo +b1x. = bo +b1x.
| (2.2) |
Неизвестные параметры bo и b1, как правило, определяются методом наименьших квадратов: значения параметров должны доставлять минимум сумме квадратов отклонений наблюденных значений yi от теоретических значений 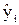 , определяемых регрессией (2.2):
, определяемых регрессией (2.2):
S(bo, b1) = å ( 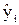 - yi)2 = å (bo +b1xi - yi)2 ® min. - yi)2 = å (bo +b1xi - yi)2 ® min.
| (2.3) |
Теоретически для оценки параметров bo и b1 можно использовать и метод наименьших модулей отклонений å ç 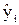 - yiç. Однако метод наименьших квадратов (МНК), во-первых, проще, во-вторых, его применение обосновывается законом больших чисел, в-третьих, позволяет проводить глубокий анализ качества эконометрической модели.
- yiç. Однако метод наименьших квадратов (МНК), во-первых, проще, во-вторых, его применение обосновывается законом больших чисел, в-третьих, позволяет проводить глубокий анализ качества эконометрической модели.
Для отыскания значений параметров bo и b1 эконометрической модели (2.2) с помощью МНК приравниваем нулю частные производные S по bo и b1 и получаем систему двух уравнений:
| ¶S/¶ bo = 2å (bo +b1xi - yi) = 0 ¶S/¶ b1 = 2å (bo +b1xi - yi) xi = 0. | (2.4) |
Отсюда после преобразований получаем систему двух линейных уравнений с двумя неизвестными bo и b1:
bon + b1åxi = å yi,
boåxi + b1å 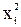 = å xi yi. = å xi yi.
| (2.5) |
Разделим 1-е уравнение на n и получим полезное соотношение: линия регрессии проходит через точку средних значений ( 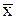 ,
, 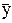 ):
):
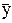 = bo +b1 = bo +b1 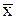 . .
| (2.6) |
Разрешая (2.6) относительно bo , подставляя это значение во 2-е уравнение системы (2.5), получим искомые формулы для расчета значений параметров уравнения регрессии:
bo = 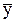 - b1 - b1 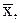 b1 =
b1 = 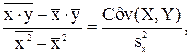
| (2.7) |
где sx2 - выборочная дисперсия переменной Х:
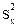 = å = å 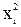 /n - ( /n - ( 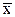 )2. )2.
| (2.8) |
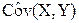 - выборочная ковариация:
- выборочная ковариация:
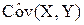 = å xi yi /n - = å xi yi /n - 
| (2.9) |
Параметр b1 называется коэффициентом регрессии (выборочным). Он показывает, на сколько единиц в среднем возрастет (уменьшится) 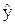 при увеличении х на одну единицу.
при увеличении х на одну единицу.
Параметр b0 в зависимости от задачи может иметь смысл, а может и не иметь. Например, если 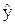 - расход электроэнергии, а х – объем производства, то параметр b0 - условно-постоянный расход электроэнергии при нулевом производстве. Если b0<0, то экономического смысла он, как правило, не имеет.
- расход электроэнергии, а х – объем производства, то параметр b0 - условно-постоянный расход электроэнергии при нулевом производстве. Если b0<0, то экономического смысла он, как правило, не имеет.
Пример 2.1 [4, с.10]. Построить уравнение парной линейной регрессии для данных табл. 2.1, где Y - расходы на покупку продовольственных товаров, % от общих расходов и Х - среднедневная зарплата, руб./чел.×сут.
Таблица 2.1
Дата добавления: 2019-10-16; просмотров: 541;
