Связь коэффициентов регрессии и корреляции
Если значение bo из формул (2.7) подставить в уравнение регрессии (2.2), то после преобразований получим уравнение регрессии в отклонениях (прямая проходит через начало координат - точку ( 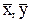 )).
)).
Преобразуем это уравнение: разделим обе части на sy, умножим и разделим правую часть на sx, получим:
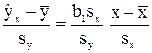 .
.
| где коэффициент r = b1 sx/sy показывает, на сколько величин sy изменится в среднем Y, если Х увеличится на одно значение sx. | (2.11) |
Другой вариант формулы для расчета r:
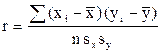 . .
| (2.12) |
Статистика r - выборочный коэффициент корреляции - отражает тесноту статистической связи случайных величин Х и Y. Свойства коэффициента корреляции (рис. 2.1):
1. -1 £ r £ 1. Чем ближе модуль ç r ç к 1, тем теснее связь Х и Y.
2. Если r = ± 1, то связь между Х и Y - функциональная и линейная.
3. Если r = 0, то линейная корреляционная связь между СВ Х и Y отсутствует.
4. Коэффициент r является непосредственной оценкой генерального коэффициента корреляции r между Х и Y лишь в случае двухмерного НЗР случайной величины (Х, У). В других случаях r не является строгой мерой взаимосвязи переменных.
у у у




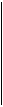


 r = +1 r » +0,8 r » +0,5
r = +1 r » +0,8 r » +0,5
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||


 х х х
х х х
а) б) в)



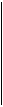
 у r = -1 у r » -0,8 у r » -0,5
у r = -1 у r » -0,8 у r » -0,5
 | |||||
 | |||||
 | |||||


 х х х
х х х
г) д) е)
Рис. 2.1. Примеры полей корреляции и значений r
Пример 2.2. По данным табл. 2.1 и примера 2.1 рассчитать значение коэффициента корреляции r. Для расчета используем формулу (2.11): r = b1 sx / sy. Неизвестные СКО sx и sy рассчитаем по формулам и данным табл. 2.1:
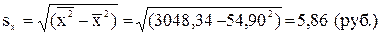 .
.
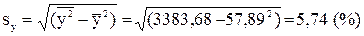 .
.
Окончательно: r = b1 sx / sy = -0,35×5.86 / 5,74 = -0,36.
Данное значение r характеризует связь между Х и Y как умеренную и обратную (см. рис. 2.1.е).
Дата добавления: 2019-10-16; просмотров: 570;
