Концепция эконометрического моделирования

Моделирование как метод познания было осознано только в начале ХХ века. В физико-технических дисциплинах начали широко применяться вещественные модели (судов, автомобилей и т.п.), результаты экспериментов с которыми на основе теории подобия переносились на оригиналы.

Показателен случай, произошедший в Англии, когда некий инженер на основе изучения поведения модели строящегося корабля в бассейне предсказал, что при спуске на воду корабль перевернется. Ему не поверили, но так и случилось. По этому поводу в Лондоне была установлена мемориальная доска с надписью: вечному порицанию невежества лордов адмиралтейства.

В экономике основой моделирования преимущественно явились знаковые модели - математические, а с середины ХХ века - еще и программно-компьютерные.

В самом общем виде модель - это мысленно представляемая или материально реализованная система, которая отображает (воспроизводит) объект исследования так, что ее изучение дает нам новые знания об этом объекте. Знаковую модель можно мыслить как теорию данного объекта: формальную или неформальную, полную или неполную, достоверную или недостоверную, противоречивую или непротиворечивую, с меньшей или с большей предсказательной силой, описательную или объяснительную, эмпирическую или теоретическую.

Математической моделью называют знаковую модель, элементами которой являются математические объекты-знаки (числа, переменные, функции, векторы, матрицы и пр.) и математические отношения между ними (сложение, дифференцирование, быть параллельными и пр.). Моделированием называют процесс исследования объекта познания на его моделях (или самих моделей), а также сам процесс построения моделей.

Существует много оснований для классификации моделей, например:

- по природе моделируемых явлений - экономические, экологические, производственные, социальные, политические и пр.;

- по форме представления - математические, механические, компьютерные и пр.;

- по воспроизводимым свойствам объектов моделирования - поведенческие, структурные, функциональные и пр.;

- по отношению ко времени - статические (время в явном виде не присутствует) и динамические;

- по свойству детерминированности либо стохастичности.

В эконометрике в основном рассматриваются объекты, которые можно представить в виде “черного ящика” (рис.1.1). Черный ящик имеет входы и зависящие от них выходы. Мы не знаем, как в действительности выходы зависят от входов. Но зато мы имеем статистические данные наблюдений по входам и выходам. На этом основании мы и строим “поведенческую” модель, достаточно хорошо (“похоже”) связывающую функционально зависимость выходов от входов. Чаще всего такой моделью является линейная функция с несколькими переменными.

Классифицируем подобную типичную эконометрическую модель. Она будет: экономическая, математическая, поведенческая, статическая или динамическая, детерминированная (хотя моделируемое явление - стохастическое).

		W
X			f(X)
				Y=f(X)+ e
Z		e

Рис. 1.1. Эконометрическая модель как черный ящик

Охарактеризуем типы переменных черного ящика:

- Х = (X₁, X₂,..., X_p) - вектор наблюдаемых, входных, существенных и потому объясняющих переменных (факторов, регрессоров, предикторов);

- Z = (Z₁, Z₂,..., Z_r) - вектор наблюдаемых, входных, несущественных переменных-факторов;

- W = (W₁, W₂,..., W_s) - вектор ненаблюдаемых, входных, несущественных переменных-факторов;

- Y - скаляр - наблюдаемая, выходная (целевая, результирующая, объясняемая) переменная;

- e - скаляр - наблюдаемая при исследовании модели и ненаблюдаемая при использовании модели (например, при прогнозировании мы не можем точно знать ошибку) выходная случайная величина - ошибка, возмущение.

Переменная Y является случайной величиной (СВ) с условной плотностью вероятностей f _{x1, x2, ... , xp}(y). Обычно делается предположение о ее нормальности (распределена по нормальному - гауссовому - закону распределения), что позволяет проводить более глубокий анализ качества эконометрической модели.

Объясняющие переменные X₁, X₂, ... , X_p могут быть как случайными, так и детерминированными. Различие между ними часто условно. Например, для пассажира интервал времени между поездами, отправляющимися с Северного вокзала на г. Светлогорск, есть СВ, а для диспетчера - строго детерминированная, предопределенная расписанием.

Классическая эконометрическая модель рассматривает вектор Х как детерминированный, однако основные результаты исследования модели остаются теми же и для случайного Х.

Таким образом, эконометрическая модель имеет вид:

В качестве представителя СВ Y естественно взять ее математическое ожидание (МО). В нашем случае мы имеем дело с условным математическим ожиданием СВ Y: М_{x1, x2, ... , xp}(Y). Как видно, М_х(Y) - так для краткости будем обозначать условное МО - является детерминированной функцией от р переменных.

Уравнение М_х(Y)=f(x₁, x₂, ... , x_p) называется уравнением регрессии. Таким образом, эконометрическая модель всегда (за исключением особых случаев) является регрессионной моделью. Обычно для любого набора значений объясняющих переменных Х при взятии математического ожидания от обеих частей (1.1) будем иметь М(e)=0 - в регрессионной модели математическое ожидание случайной ошибки равно нулю. Иначе говоря, e - центрированная СВ.

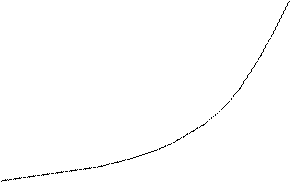
В качестве примера приведем регрессионную модель, отображающую зависимость объема потребления Y от уровня дохода Х (ден.ед./год), предложенную шведским экономистом Л. Торнквистом. Модель состоит не из одной, а из трех различных функций и дополнительного условия баланса (рис.1.2).

Y
					y3
β0						y2
	y1
						X

Рис. 1.2. Эконометрическая модель связи потребления Y и дохода X

Для предметов 1-й необходимости (питание, одежда, жилье и пр):

.

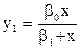(1.2)

Некоторые свойства функции у₁, которые отражают смысл явления:

- при доходе х, близком к нулю, у₁ идет вдоль биссектрисы: все доходы расходуются на предметы первой необходимости: у₁»х,

- при заметном росте доходов х потребление у₁ асимптотически приближается к пределу: у₁ =b_о .

Для предметов средней необходимости (газеты, пылесос, стиральная машина и пр):

.

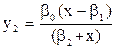(1.3)

Свойства функции у₂:

- расходы на предметы средней необходимости начинаются (у₂>0) при уровне доходов х > b₁, поэтому у₂ (и у₃ по этой же причине) требует доопределения;

- при значительном росте доходов х потребление у₂ асимптотически приближается к тому же пределу у₂ =b_о;

- из второго свойства вытекает: пределы расходов на предметы первой и средней необходимости равны между собой (это частный случай конкретной экономики).

Для предметов роскоши (предметы искусства, драгоценности, престижный дом и пр.):

.

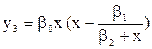(1.4)

Свойство функции у₃:

- расходы у₃ на предметы роскоши при неограниченном увеличении доходов х также неограниченно увеличиваются.

Теперь заметим, что если доходы х расходуются только на цели у₁, у₂, у₃, то сумма последних должна в точности быть равной доходам. Так мы приходим к 4-й - совместной - функции в исследуемой эконометрической модели (см. подробнее параграф 1.3: системы совместных уравнений):