Система обслуживания M/G/1.
Здесь процесс поступлений – пуассоновский, система – однолинейная, ёмкость накопителя бесконечная, распределение времени обслуживания – произвольное, т. е. пакеты имеют случайную произвольно распределенную длительность.
Так как предполагается общий характер статистики времени обслуживания и, соответственно, невыполнение условия отсутствия последействия уходов обслуженных клиентов, здесь нельзя использовать уравнения равновесия.
Будем использовать подход, основанный на рассмотрении занятости накопителя:
Пусть 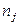 – число клиентов, остающихся в системе, если j –ый клиент покинул систему.
– число клиентов, остающихся в системе, если j –ый клиент покинул систему.
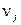 - число клиентов, поступающих за время обслуживания j – го клиента.
- число клиентов, поступающих за время обслуживания j – го клиента.
Тогда 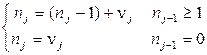 , (2.41)
, (2.41)
или 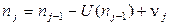 , (2.42)
, (2.42)
где U(x) – единичная функция. 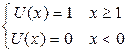 .
.
Выражение (2.42) может быть записано и в других обозначениях, которые упростят запись некоторых используемых ниже формул. Вводя
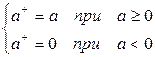 ,
,
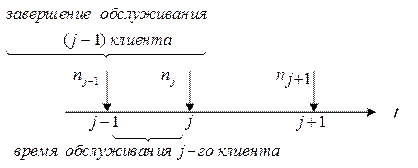
Рис. 2.16. Анализ состояния накопителя.
(2.42) перепишем в виде
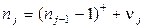 . (2.43)
. (2.43)
Здесь в (2.42) и в (2.43) 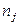 и
и 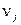 независимые случайные величины.
независимые случайные величины.
Распределение вероятностей nj – это распределение суммы случайных величин, найти которое довольно сложно, потому что при непосредственных вычислениях оно находиться как свёртка распределений. Чтобы упростить вычисление используется аппарат производящих функций.
В первой главе уже было использовано это понятие, однако, здесь напомним, что для дискретной случайной величины n производящая функция имеет вид:
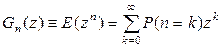 , (2.44)
, (2.44)
где z – произвольное комплексное число, но такое, которое, дает сходимость в (2.44).
Обозначая 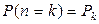 , получим
, получим
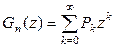 . (2.45)
. (2.45)
Отметим, что свёртке распределений соответствует произведение производящих функций. Если w=x+y, то 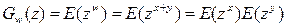 .
.
Напомним, что из (2.45) следует:
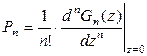 , (2.46)
, (2.46)
т. е. Pn, являющиеся вероятностями состояния системы, могут быть найдены из разложения Gn(z) в ряд по степеням z.
Зная Pn, можно определить и другие характеристики системы. Из (2.43) следует
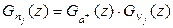 , (2.47)
, (2.47)
где под величиной а+ подразумевается 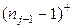 .
.
Функцию распределения величины 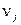 будем считать известной, поэтому
будем считать известной, поэтому 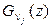 всегда можно определить. Будем также предполагать, что в системе возможен стационарный режим и при этом индекс j можно опустить.
всегда можно определить. Будем также предполагать, что в системе возможен стационарный режим и при этом индекс j можно опустить.
Найдём 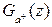 согласно (2.45)
согласно (2.45)
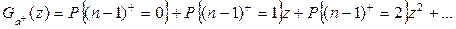 . (2.48)
. (2.48)
Из определения величины а+ следует, что
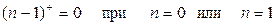 и
и
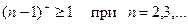
Поэтому: 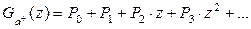
Из сравнения с 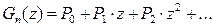 следует
следует 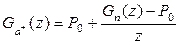 . (2.49)
. (2.49)
Подставляя (2.49) в (2.47) получим:
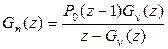 . (2.50)
. (2.50)
В (2.50) величина P0 пока неизвестна. Ее можно определить из условия, аналогичного условию нормировки,
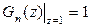 .
.
При 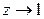 в (2.50) возникает неопределенность типа
в (2.50) возникает неопределенность типа 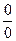 , т. к.
, т. к. 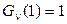 , по определению. Раскрыть неопределённость можно, разложив
, по определению. Раскрыть неопределённость можно, разложив 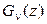 в ряд Тейлора в окрестности точки z=1.
в ряд Тейлора в окрестности точки z=1.
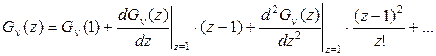 (2.51)
(2.51)
Вычислим производные, входящие в (2.51)
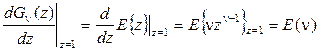 , (2.52)
, (2.52)
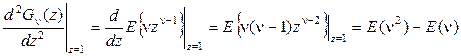 .(2.53)
.(2.53)
Последовательное дифференцирование позволяет получить различные моменты случайной величины 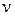 . Именно поэтому
. Именно поэтому 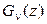 называют производящей функцией моментов.
называют производящей функцией моментов.
Теперь:
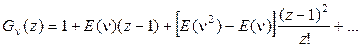 (2.54)
(2.54)
С учетом полученного выражения знаменатель выражения (2.50) примет вид
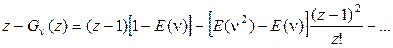 (2.55)
(2.55)
Подставляя (2.55) в (2.50) и положив z=1, с учётом 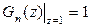 получим
получим
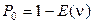 . (2.56)
. (2.56)
(Сравним: для системы M/M/1 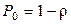 )
)
Теперь для 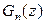 можно окончательно получить:
можно окончательно получить:
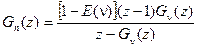 . (2.57)
. (2.57)
Воспользуемся выражением (2.57) для анализа системы M/D/1.
Как следует из обозначения, на входе системы действует пуассоновский поток пакетов и, все пакеты имеют одинаковую длину 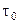 . При пуассоновских поступлениях с интенсивностью
. При пуассоновских поступлениях с интенсивностью 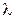 вероятность того, что за время обработки одного пакета в систему поступит k пакетов определится в виде
вероятность того, что за время обработки одного пакета в систему поступит k пакетов определится в виде
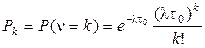 , (2.58)
, (2.58)
где 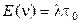 . (2.59)
. (2.59)
Предполагается, что 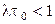 , т. к. это ограничивает скорость поступлений. Это условие эквивалентно условию
, т. к. это ограничивает скорость поступлений. Это условие эквивалентно условию 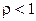 для системы M/M/1. А величину
для системы M/M/1. А величину 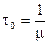 можно интерпретировать как среднюю длину сообщения при экспоненциальном времени обслуживания в системе M/M/1. Ограничение
можно интерпретировать как среднюю длину сообщения при экспоненциальном времени обслуживания в системе M/M/1. Ограничение 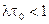 , как
, как 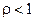 , даёт гарантию режима статистического равновесия.
, даёт гарантию режима статистического равновесия.
Для пуассоновского распределения вида (2.58) производящая функция имеет вид (с учетом разложения 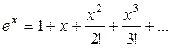 )
)
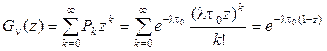 . (2.60)
. (2.60)
Вычисление производной производящей функции подтверждает известный результат для пуассоновского распределения
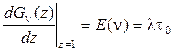 .
.
Теперь для системы M/D/1 подставляя (2.60) в (2.57) получаем выражение производящей функции для случайной величины n в рассматриваемой модели (2.41)
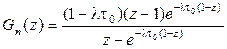 . (2.61)
. (2.61)
Дифференцируя (2.61) можно найти среднюю занятость системы M/D/1, а разлагая в ряд по степеням z можно найти вероятности занятия буферной памяти. К сожалению, разложение 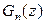 в ряд в общем случае представляет собой довольно сложную задачу.
в ряд в общем случае представляет собой довольно сложную задачу.
Вернёмся к системе M/G/1.
Найдём 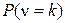 - вероятность поступления ровно k пакетов за случайное время обслуживания
- вероятность поступления ровно k пакетов за случайное время обслуживания 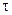 . Пусть
. Пусть 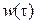 - плотность распределения
- плотность распределения 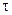 . Тогда:
. Тогда:
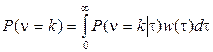 . (2.62)
. (2.62)
В выражении (2.62) 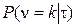 - вероятность поступления k пакетов при условии фиксации конкретного значения
- вероятность поступления k пакетов при условии фиксации конкретного значения 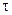 (условная вероятность). Для пуассоновского потока
(условная вероятность). Для пуассоновского потока
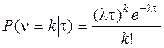 .
.
Знание 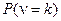 позволит найти порождающую функцию моментов для случайной величины n. Для
позволит найти порождающую функцию моментов для случайной величины n. Для 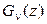 теперь можно записать
теперь можно записать 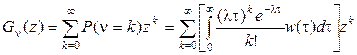 .
.
Изменяя порядок суммирования и интегрирования с учётом того, что под знаком суммы – экспонента, получим:
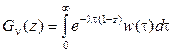
Данный интеграл представляет собой преобразование Лапласа плотности вероятности 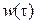 . (Напомним, по определению преобразование Лапласа в данном контексте может быть записано как
. (Напомним, по определению преобразование Лапласа в данном контексте может быть записано как 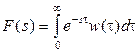 , где s – комплексная переменная. Кроме того, если s принимает только мнимые значения, то преобразование Лапласа и преобразование Фурье совпадают, что позволяет нам считать производящую функцию аналогом характеристической функции). С учетом этого замечания последнее выражение для
, где s – комплексная переменная. Кроме того, если s принимает только мнимые значения, то преобразование Лапласа и преобразование Фурье совпадают, что позволяет нам считать производящую функцию аналогом характеристической функции). С учетом этого замечания последнее выражение для 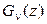 запишется в виде
запишется в виде
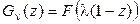 . (2.63)
. (2.63)
Конкретный вид функции 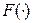 определяется, естественно, заданной плотностью
определяется, естественно, заданной плотностью 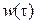 .
.
Например, все сообщения имеют одинаковую длину 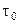 , что соответствует системе M/D/1. Тогда
, что соответствует системе M/D/1. Тогда 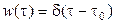 . Подставляя эту плотность в выражение для
. Подставляя эту плотность в выражение для 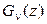 , получаем результат в виде (2.60).
, получаем результат в виде (2.60).
Если 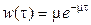 , что соответствует системе M/M/1, то преобразование Лапласа этой плотности дает
, что соответствует системе M/M/1, то преобразование Лапласа этой плотности дает 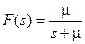 , и для порождающей функции
, и для порождающей функции 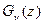 получаем
получаем
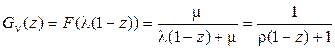 .
.
Можно привести и другие примеры.
Зная порождающую функцию 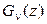 из (2.63) можно найти
из (2.63) можно найти 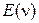 . По определению:
. По определению:
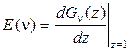 .
.
Но из (2.63)
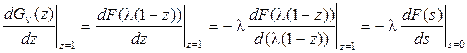 .
.
Далее, т.к. 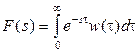 , то
, то 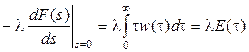 .
.
Поэтому
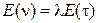 . (2.64)
. (2.64)
Если 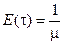 - как в системе M/M/1, то
- как в системе M/M/1, то 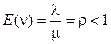 . Теперь из (2.56)
. Теперь из (2.56) 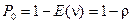 , что ранее было получено другим способом, и из (2.57)
, что ранее было получено другим способом, и из (2.57)
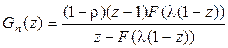 . (2.65)
. (2.65)
Проверим формулу (2.65). Для системы M/M/1
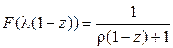 .
.
Тогда 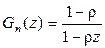 - здесь
- здесь 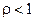 и
и 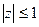 , что необходимо для схо-димости
, что необходимо для схо-димости 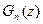 .
.
Разложим 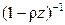 в ряд по степеням z:
в ряд по степеням z:
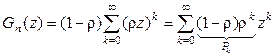 .
.
Коэффициент при zk – это Pk, т. е. 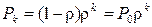 , что было получено ранее.
, что было получено ранее.
Теперь найдём Е(n) – среднее число сообщений в буфере.
Зная порождающую функцию 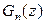 , это можно сделать согласно ее свойствам:
, это можно сделать согласно ее свойствам:
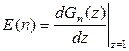 .
.
При этом выражение для 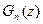 возьмем из общей формулы (2.57):
возьмем из общей формулы (2.57): 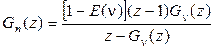 .
.
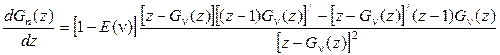 .
.
При вычислении Е(n) по последней формуле следует следить за тем, чтобы подстановка z=1 не привела к возникновению неопределенности типа 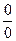 . Покажем подробнее, как это следует сделать.
. Покажем подробнее, как это следует сделать.
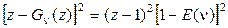
Из (2.55):
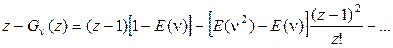
Далее
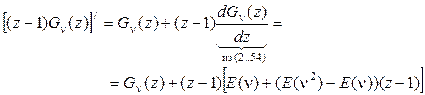 .
.
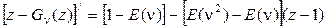 .
.
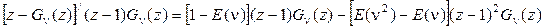
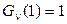 .
. 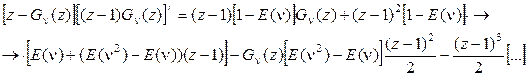
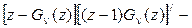
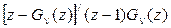 ={сократим сразу на
={сократим сразу на 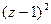 и подставим z=1}=
и подставим z=1}=
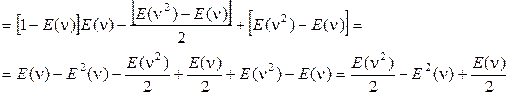
С учётом 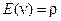
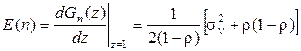 , (2.66)
, (2.66)
где 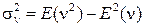 - дисперсия случайной величины
- дисперсия случайной величины 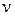 .
.
2.6. Упрощенный вывод формулы для Е(n)
Системы M/G/1
Строгий вывод формулы для E(n) через производящую функцию, как видно, довольно сложен. Проще E(n) можно получить из (2.42).
Возведём (2.42) в квадрат, возьмём математическое ожидание от обеих частей и положим 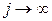 :
:
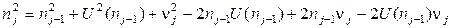 . (*)
. (*)
При 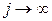 из (2.42) следует
из (2.42) следует 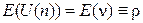 .
.
Кроме того: 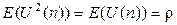 и
и 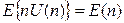 - оба равенства следуют из определения U(n).
- оба равенства следуют из определения U(n).
Будем считать, что 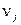 и
и 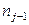 независимы, тогда
независимы, тогда
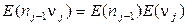 .
.
С учетом сделанных замечаний формулу (*) перепишем в виде: 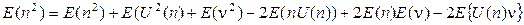
Учтем также, что 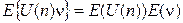 т. к. случайные величины n и n независимы. Теперь
т. к. случайные величины n и n независимы. Теперь
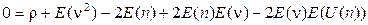 ,
,
откуда 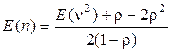 .
.
Т.к. 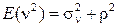 , то для E(n) окончательно запишем
, то для E(n) окончательно запишем
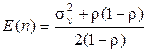 ,
,
что совпадает с (2.66)
Здесь 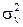 - дисперсия числа клиентов, поступающих в течение времени обслуживания.
- дисперсия числа клиентов, поступающих в течение времени обслуживания.
Найдём 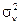 . По определению дисперсии
. По определению дисперсии
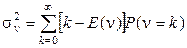 . (2.67)
. (2.67)
Поток заявок на обслуживание пуассоновский, поэтому для 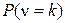 используем выражение (2.62), а
используем выражение (2.62), а 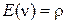 , поэтому
, поэтому
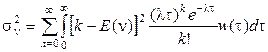 . (2.68)
. (2.68)
Изменим порядок интегрирования и суммирования с учётом следующих соотношений:
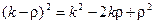 ,
,
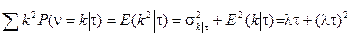 ,
,
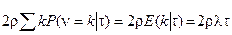 ,
,
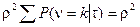 .
.
В последних трех формулах использованы свойства распределения Пуассона. Теперь (2.68) преобразуется к виду
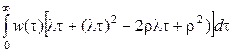 .
.
Если в последней формуле учесть, что
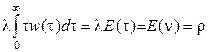 ,
,
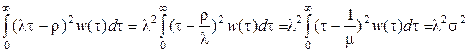 ,
,
то для 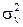 можно окончательно записать
можно окончательно записать
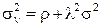 , (2.69)
, (2.69)
где 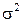 - дисперсия распределения времени обслуживания.
- дисперсия распределения времени обслуживания.
Подставим теперь (2.69) в (2.66):
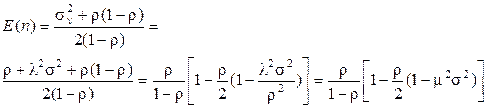 ,
,
т. е. 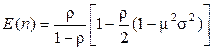 . (2.70)
. (2.70)
Формула (2.70) называется формулой Поллячека-Хинчина. Из формулы Литтла
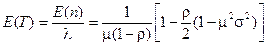 . (2.71)
. (2.71)
Здесь 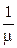 - среднее время обслуживания.
- среднее время обслуживания.
В системе M/M/1 время обслуживания распределено экспоненциально. Дисперсия этого распределения 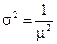 . Подставляя в (2.70), получаем:
. Подставляя в (2.70), получаем: 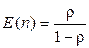 , что совпадает с полученным ранее.
, что совпадает с полученным ранее.
Для системы M/D/1 все клиенты требуют одного времени обслуживания 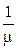 , при этом
, при этом 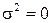 . Тогда:
. Тогда:
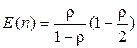 , (2.72)
, (2.72)
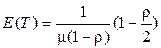 .
.
Можно считать, что система M/D/1 - это частный случай M/M/1 с наименьшей длиной очереди и задержкой.
В заключение найдем среднее время ожидания E(W) для M/G/1:
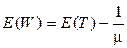 .
.
Подставим сюда E(T) из (2.71):
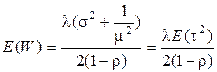 , (2.73)
, (2.73)
где 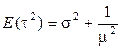 - второй момент распределения времени обслуживания.
- второй момент распределения времени обслуживания.
Дата добавления: 2019-04-03; просмотров: 1288;
