Система с «нетерпеливыми» клиентами.
Это - система с управлением входным потоком.
Здесь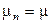 
и 
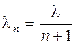. Доступна одна обслуживающая линия, и, когда очередь становится большой – клиенты уходят. Для передачи пакетов это означает, что контроллер системы либо отводит новые поступления, либо блокирует систему, что приводит к уменьшению интенсивности поступлений.
Нетрудно убедиться, что из общей формулы (2.24) легко для данной системы получить
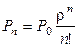, где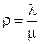 
. Значит в этой системе 
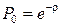, и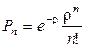 
. Следовательно
.
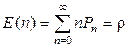Производительность системы, определенная «по входу», запишется как
.
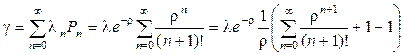С учетом того, что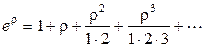 
последнее выражение примет вид
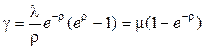. (2.34)
Этот результат можно получить и по-другому, если учесть, что для однолинейной системы с интенсивностью обслуживания m производительность равна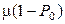 
. Но здесь 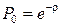, что и дает результат (2.34).
Зная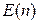 
и g можно найти нормированное среднее время задержки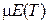 
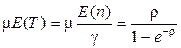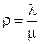, . (2.35)
При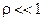 
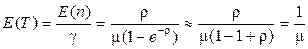, (с учетом 
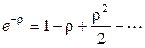), т.е. задержка приближенно равна времени обслуживания и 
.
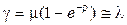Система остается стабильной и при больших r, т.к. существует управление потоком. При этом растет средняя занятость системы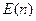 
и наиболее вероятны состояния с большими значениями n.
Система M/M/N/0.
Это частный случай системы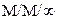 
с конечным числом обслуживающих линий и без мест для ожидания (без накопителя) – см. рис.2.15.
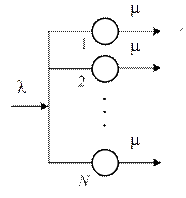
Рис. 2.15. Система M/M/N/0.
Здесь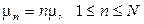 
и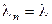 
. При n=N все поступления блокируются. Мест для ожидания нет и поэтому – это система с потерями. Данная система является базовой моделью для анализа телефонных станций.
Для системы 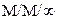было получено 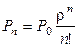, где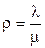 
. Здесь условие нормировки имеет вид 
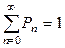. Подставляя сюда 
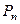получаем
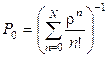, и возвращая теперь 
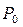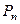в имеем
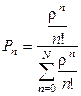. (2.36)
Блокировка наступает при n=N. Поэтому
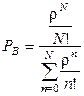. (2.37)
Формула (2.37) – это распределение Эрланга 1-го рода или В-распределение.
Найдем среднюю занятость системы.
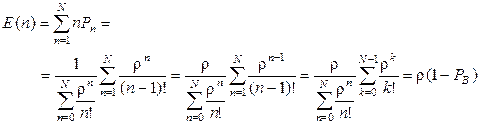, т.е.
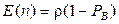. (2.38)
При увеличении r вероятность блокировки стремится к единице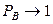 
и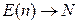 
.
Производительность g, определенная «по входу», равна
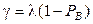, (2.39) или – «по выходу : 
.
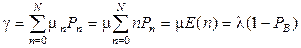При увеличении r производительность стремится к своему максимальному значению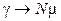 
. Это происходит тогда, когда 
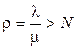, большинство вызовов блокируется и .
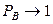Средняя задержка вызовов, которые приняты системой равна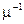 
, т.е.среднему времени обслуживания (продолжительности занятия). Это подтверждает формула Литтла
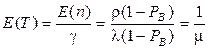. (2.40)
Дата добавления: 2019-04-03; просмотров: 511;