Согласно формуле Литтла

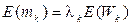, (2.86)

где 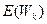- среднее время ожидания.

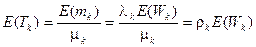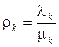, . (2.87)

Аналогично 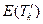- возникает за счет поступления в среднем 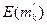клиентов класса k в течение промежутка 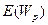.Интенсивность поступлений - 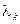, время обслуживания - 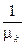, поэтому

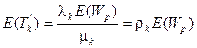. (2.88)

Подставим 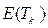и в (2.84)

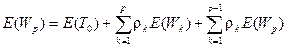
или: 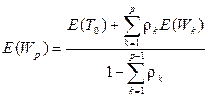. (2.89)

Решать эти уравнения следует рекуррентно, начиная с высшего класса:

для p=1 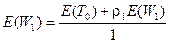, откуда следует

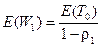, (2.90)

для p=2 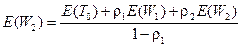. В последнюю формулу подставим 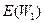и получим

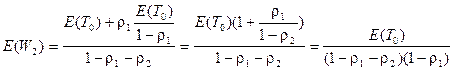. (2.91)

Этот процесс можно продолжить, перебирая все более высокие значения р. В общем виде формула для 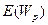будет иметь вид

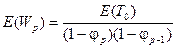, (2.92)

где ,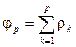

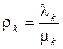
В (2.92) осталась не определенной одна составляющая - 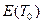. Определим ее. Для этого рассмотрим систему M/G/1 с одним классом требований.

Сравним (2.90) и (2.73), т.е. 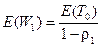и 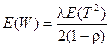. Из сравнения следует

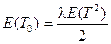. (2.93)

В более общем случае для системы с несколькими классами требований (r)

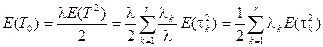. (2.94)

Вернемся к примеру в начале раздела. Очевидно, управляющим пакетам можно присвоить 1 класс приоритета, а пакетам данных – 2. При 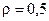из (2.90) и (2.91) следует: 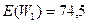мс, 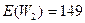мс. В системе без приоритетов E(W)=148мс. Таким образом, влияние на время ожидание пакетов 2-го класса в системе с приоритетами пренебрежимо мало, зато 1-ый класс выиграл в 2 раза.

При введении приоритетов действует закон сохранения, который формально можно отобразить соотношением

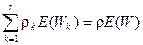, (2.95)

где E(W) - время ожидания в системе M/G/1 с дисциплиной обслуживания FIFO. Это время находится согласно формуле (2.73). В нашем примере при отсутствии приоритетов

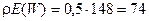мс.

При введении приоритетов: 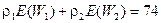мс.

Закон сохранения установлен Л. Клейнроком и является частным случаем более общего закона для систем с сохранением работы.

Литература:

1. Хинчин А. Я. Работы по математической теории массового обслуживания. – М.:Физматгиз, 1963г.

2. Саати Т. Л. Элементы теории массового обслуживания и её приложения.- М.:Сов. Радио, 1965г.

3. Кофман Л., Крюон Р. Массовое обслуживание. Теория и приложения. – М.: Мир, 1965г.

4. Клейнрок Л. Теория массового обслуживания. – М.:Машиностроение, 1979г.

5. Овчаров Л. А. Прикладные задачи теории массового обслуживания.- М.: Машиностроение, 1969г.

6. Шварц М. Сети связи. Том 1. – М.: Наука, 1992г.

7. Шварц М. Сети ЭВМ. Анализ и проектирование.-М.: Сов.Радио, 1981г.

8. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений.-М.: Наука, 1971г.