Система обслуживания М/М/1.

Центральным понятием при анализе любой системы является ее состояние, причем под состоянием понимается количество клиентов (пакетов) в системе n, включая клиента, находящегося на обслуживании. Очевидно, n является случайной величиной и задача заключается в определении вероятности любого состояния системы в произвольный момент времени 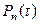. Если вероятности состояний найдены, то статистические свойства системы (например, среднее время занятия, вероятность блокировки для конечной очереди, средняя пропускная способность и др.) могут быть определены сравнительно просто.

Пусть есть система М/М/1, изображенная на рис. 2.2а.

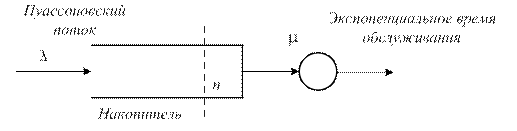
а)

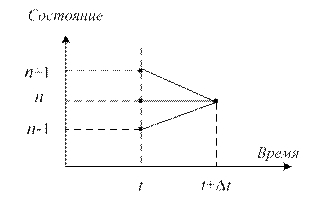
б)

Рис.2.2. Система обслуживания М/М/1 и диаграмма ее состояний.

Интенсивность пуассоновского потока на входе - l, а процесс обслуживания (длина пакета или продолжительность соединения) описывается экспоненциальным распределением с параметром μ, которое имеет вид

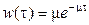. (2.1)

Найдём 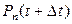- вероятность того, что в момент 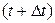в системе будет находиться n клиентов. В силу ординарности входного потока 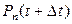есть сумма вероятностей состояний (взаимно исключающих) n-1, n или n+1, в которых система могла быть в момент t (см. диаграмму на рис.2.2б), умноженных на независимые вероятности попадания в состояние n за время Δt.

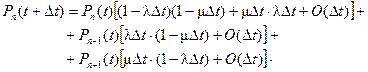(2.2)

При записи (2.2) учтено, что если время обслуживания имеет экспоненциальное распределение, то поток моментов времени завершения обслуживания является пуассоновским потоком. Поэтому вероятность завершения обслуживания за время Δt есть 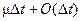, и, соответственно, вероятность не завершения обслуживания за время Δt равна 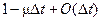. Первая строка (2.2), к примеру, характеризует переход 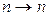, который может произойти либо при одном поступлении и одном уходе – вероятность чего записывается как 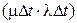, либо, если не будет ни поступления, ни ухода с вероятностью .

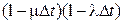Преобразуя (отбрасывая члены, пропорциональные 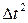), получим:

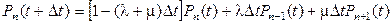. (2.3)

Уравнение (2.3) позволяет исследовать переходный режим системы. Разложим 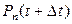в ряд Тейлора и удержим в ряде два члена

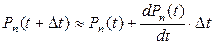. (2.4)

Подставляя (2.4) в (2.3), получим

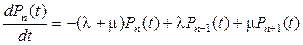. (2.5)

Стационарное значение 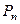можно найти из условия 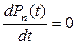. При этом из (2.5) имеем:

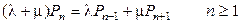. (2.6)

Это уравнение равновесия. Левая часть описывает уходы из состояния n, правая – приходы в состояние n. Графически последовательность состояний и возможные переходы из состояния в состояние отражены на рис.2.3. Состояния отображаются пронумерованными точками, а переходы – стрелками.

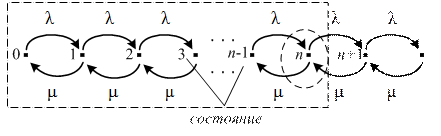
Рис.2.3. Диаграмма состояний системы М/М/1.

Пунктиром на рисунке отмечены две области: овальная область (область 1), охватывающая состояние равновесия n, и прямоугольная область (область 2), охватывающая все состояния от 0 до n . Если для области 1 в состоянии равновесия приравнять исходящий поток (интенсивность уходов из состояния n) входящему потоку (интенсивность прихода в состояние n), то получим уравнение (2.6). Значит, эта диаграмма позволяет не только составить уравнение (2.6), но и решить его. Для этого рассмотрим область 2. Поток, поступающий в эту область: 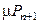, поток, покидающий его: 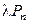. Поэтому:

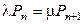. (2.7)

Уравнение (2.7) выполняется для любого n и удовлетворяет уравнению (2.6), следовательно, может рассматриваться как его решение. Перебирая n, можно записать решение в явном виде: 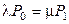, откуда 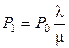, далее 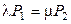, 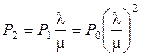и т.д.

В результате получаем 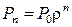, где 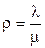, а P₀ можно найти из условия нормировки .

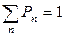Для бесконечной очереди: .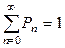

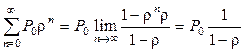. Здесь использована формула суммы членов геометрической прогрессии, конечный результат в которой достигается при 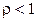. Поэтому

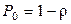, (2.8)

и 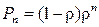. (2.9)

Итак, равновесие в системе возможно при 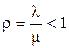. Распределение (2.9), характеризующее систему M/M/1, называется геометрическим распределением. Оно представлено на рис.2.4.

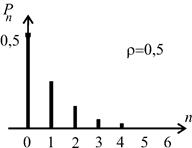
Рис.2.4. Геометрическое распределение.

В силу того, что 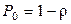(т.е. вероятность того, что система пуста, n=0), вероятность того, что система не пуста 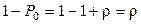т.е. равна коэффициенту нагрузки.

Для конечной очереди N уравнение равновесия (2.6) справедливо для всех n, кроме двух граничных точек: n=0 и n=N. Уравнение (2.7) справедливо всегда. Из условия нормировки: 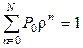, которое после вычисления суммы запишется как 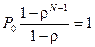, получаем Р₀

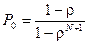. (2.10)

Поэтому для конечной очереди из N пакетов в системе M/M/1:

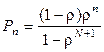. (2.11)

Вероятность того, что очередь заполнена: 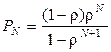. Эта вероятность, по – другому, есть вероятность блокировки, т. е. вероятность того, что пакеты не могут быть приняты системой, т.к. накопитель заполнен. Проиллюстрируем это понятие.