Задание линейных кодов с помощью порождающих и проверочных матриц
Линейные коды задаются с помощью порождающей G(x) и проверочной H(x) матриц. Эти матрицы связаны основным уравнением кодирования:
G(x)×H(x)T=0.
Матрица G(x) содержит k строк и n столбцов, ее элементами являются нули и единицы. В качестве строк матрицы G(x) выбираются любые ненулевые линейно независимые n-значные векторы, отстоящие друг от друга не менее чем на заданное кодовое расстояние d0.
Векторы v1, v2, …, vk называются линейно независимыми, если выполняется условие
c1 v1 + c2 v2 +…+ck vk = 0,
где сi={0, 1}, а сложение выполняется по модулю два. То есть, каким бы образом мы не суммировали различные строки матрицы G(x), не получим суммы, равной нулю. Все множество кодовых слов состоит из строк порождающей матрицы и всевозможных комбинаций этих строк, т.е. суммы по модулю два всех строк матрицы G(x) сначала попарно, затем по три и так далее до суммы всех k строк.
С точки зрения алгебры все кодовые слова образуют некоторое векторное пространство, базисом которого являются строки матрицы G(x).
Поскольку линейно независимые векторы могут быть выбраны произвольным образом, то, очевидно, можно построить множество матриц G(x) с одним и тем же кодовым расстоянием d0.
Свойство линейной независимости векторов инвариантно относительно двух следующих операций (выполняя эти две операции, кодовое расстояние не меняется):
1) возможна произвольная перестановка строк и столбцов в матрице G(x);
2) замена i-й строки на сумму i-й и j-й строк и т. д. (эту операцию нельзя осуществлять со столбцами матрицы G(x)).
Производя вышеуказанные операции, любую произвольную матрицу G(x) можно привести к так называемому приведенно-ступенчатому (каноническому) виду:
|

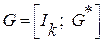
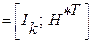 k , (1)
k , (1)
где Ik –единичная подматрица размерностью k×k,
H*T – транспонированная проверочная матрица (транспонировать – значит поменять местами строки и столбцы).
Исходя из основного уравнения кодирования, проверочная матрица имеет вид
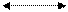

|
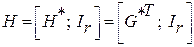 (2)
(2)
|
Пример:
Возьмем порождающую матрицу кода (7,4). В этой матрице количество строк равно 4 (k=4), а количество столбцов 7(n=7).
1 0 0 0 1 0 1
G(x)=0 1 0 0 1 1 1
0 0 1 0 1 1 0
0 0 0 1 0 1 1
Для того чтобы построить проверочную матрицу, необходимо транспонировать подматрицу G(x)* и к ней приписать единичную матрицу размером l×l. Проверочная матрица будет иметь размер l×n, l = n-k=7-4=3, т.е. матрица Н(x) имеет размер 3×7.
1 1 1 0 1 0 0
H(x)=0 1 1 1 0 1 0
1 1 0 1 0 0 1
Дата добавления: 2019-04-03; просмотров: 2336;
