Кодирование информации линейным блоковым кодом

Операция кодирования информации линейным кодом заключается в умножении информационного вектора A_k размерностью k на порождающую матрицу G(x); в результате получаем вектор

F(x)=A_k(x)×G(x).

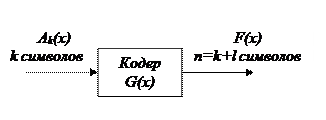
Кодовую последовательность на выходе кодера можно записать в виде:

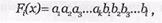
где a₁a₂a₃...а_k - информационные символы (логические 1 и 0),

b₁b₂b₃...b₁ - проверочные символы (логические 1 и 0).

Проверочные символы b₁b₂b₃...b_l формируются путем суммирования по модулю два информационных символов, стоящих на определенных позициях.

где c_j1c_j2...c_jk- коэффициенты принимающие значение логических 1 и 0.

Пример: A_k(x)=1010

1 0 0 0 1 0 1

G(x)=0 1 0 0 1 1 1

0 0 1 0 1 1 0

0 0 0 1 0 1 1

1 0 0 0 1 0 1

Следовательно, F(x)=A_k(x)×G(x)=[1010]* 0 1 0 0 1 1 1 = [1010 011]

0 0 1 0 1 1 0

0 0 0 1 0 1 1

Рассмотрим построение и реализацию устройства кодирования ЛБК (7,4).

Порождающая и проверочная матрицы этого кода имеют вид:

а₁а₂а₃а₄ b₁b₂b₃

1 0 0 0 1 0 1 1 1 1 0 1 0 0

G(x)=0 1 0 0 1 1 1 H(x)=0 1 1 1 0 1 0

0 0 1 0 1 1 0 1 1 0 1 0 0 1

0 0 0 1 0 1 1

Этот код имеет d=3 и исправляет все одиночные ошибки и обнаруживает двойные. Символы а₁,а₂,а₃,а₄ – информационные символы, b₁,b₂,b₃ – проверочные.

По матрице запишем проверочные уравнения:

b₁= a₁Åa₂Åa₃

b₂= a₂Åa₃Åa₄

b₃= a₁Åa₂Åa₄

Таким образом, кодер состоит из (n-k)=7-4=3 сумматоров по модулю два, выходы которых соответствуют (n-k) проверочным символам.

Устройство кодирования линейного группового кода (7, 4) приведено на рисунке.

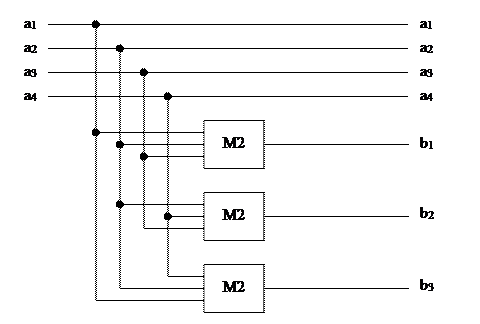
Рисунок – Кодер линейного группового кода (6, 3)

Пусть подается сообщение (а₁,а₂,а₃,а₄)=1001. Тогда слово, передаваемое в канал связи, имеет вид (1001 110).