Синдромное декодирование

Декодирование более сложный процесс, чем кодирование.

Декодирование линейных групповых кодов основано на следующем свойстве: Проверочная H(х) и порождающая G(х) матрицы удовлетворяют соотношению G(х)*H^t(х)=0, где H^t(х) - транспонированная проверочная матрица.

Если в принятом слове F(х) отсутствуют ошибки, то матричное произведение равно нулю.

F(х)*H^t(х)=A_k(x)*G(x)*H^t(х)= A_k(x)*0=0

Ecли же при передаче информации возникли ошибки, то (F+E)*H^t=F*H^t+E*H^t=0+E*H^t=E*H^t=S – синдром, где E – вектор ошибки. Длина синдрома равна (n-k). Ненулевая величина синдрома свидетельствует о наличии ошибки. Если различным ошибкам соответствуют различные синдромы, то по виду синдрома можно определить вид ошибки и, следовательно, исправить ее.

Этапы декодирования:

1. По принятому слову

S_j(x)= F(x)^* × H^t(x).

2. По синдрому S_j(x) находится вектор ошибок E.

3. Из принятого вектора F(x)^* вычитается вектор ошибок; в результате получаем переданное слово, F(x).

Синдромный декодер состоит из схемы, вычисляющей (n-k)-разрядный синдром, дешифратора и корректирующих сумматоров по модулю два. Схема вычисления синдрома производит умножение принятого вектора на матрицу H^t(x). При отсутствии ошибок синдром равен нулю. Если синдром не равен нулю, то возбуждаются соответствующие выходы дешифратора и сигналы с ошибочных разрядов исправляются на корректирующих сумматорах.

Схема синдромного декодера кода (6, 3) представлена на рисунке.

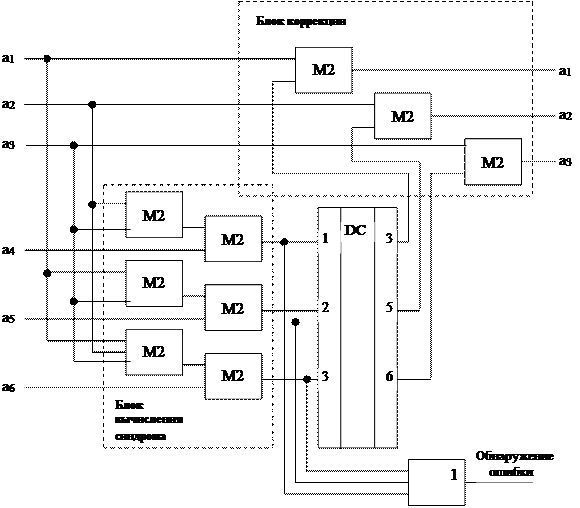Рисунок – Схема синдромного декодера кода (6, 3)

Пусть F(x)=111 001, например, ошибка произошла в первом разряде, т.е. принятое слово имеет вид F(x)^*=(011 001).

Вычислим синдром S_j(x)= F(x)^* ×H^t(x).

а₁а₂а₃ а₄а₅а₆

0 1 1 1 0 0 011

H(x) =1 0 1 0 1 0 H^t(x)= 101 S_j(x)= F(x)^* ×H^t(x)=011

1 1 1 0 0 1 111

Синдром равен 011 (это первая строчка матрицы H^t(x), следовательно, ошибка произошла в первом разряде) и на первом выходе дешифратора должен появиться единичный сигнал, который исправит на первом корректирующем сумматоре ошибочный сигнал на противоположный – правильный. Это обеспечит получение на выходе приемника сигнала A_k(x)=111, который и передался в канал связи.

В том случае, если требуется только обнаружение ошибок, то сигналы с выхода схемы вычисления синдрома заводится на схему ИЛИ. На выходе схемы ИЛИ будет единичный сигнал в случае ненулевого синдрома, что свидетельствует о наличии ошибок в принятом сообщении.

Декодирование по синдрому применяется для коррекции ошибок малой кратности. Основная трудность при декодировании по синдрому связана с ''проблемой селектора'', который по синдрому должен однозначно установить разряды, в которых произошли ошибки, т. е. определить вектор ошибок E.