Свойства циклических кодов
ЦК обладают всеми свойствами СЛБК, а также имеют, ряд дополнительных свойств.
К основным свойствам ЦК относятся:
1. Вес разрешенной кодовой последовательности wкп≥d0;
2. Вес проверочной части разрешенной кодовой последовательности wпр.ч.≥d0-1;
3. Сдвиг кодовых символов разрешенной кодовой последовательности влево или вправо на один, два,..., (k-1) символ вновь приводит к разрешенной кодовой последовательности. Если же при циклическом сдвиге всегда будет получатся кодовая последовательность нового кода, то такой код будет называться квазициклическим; данные коды имеют несколько большую корректирующую способность и сложность реализации, чем ЦК;
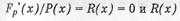 4. Разрешенная кодовая последовательность без ошибок Fp'(x) при делении на полином Р(х)дает нулевой остаток ≠0 при наличии ошибок;
4. Разрешенная кодовая последовательность без ошибок Fp'(x) при делении на полином Р(х)дает нулевой остаток ≠0 при наличии ошибок;
5. Сумма по модулю два символов двух, трех,..., (k-1)разрешенных кодовых последовательностей вновь образует разрешенную кодовую последовательность;
6. Двучлен вида хп+1 должен делиться на порождающий полином Р(х) без остатка и результат дает проверочный полином h(x) =(хп+1)/Р(х. Произведение h(x)*P(x)=хn+1=0, а потому полиномы h(x) и Р(х) рассматривается как ортогональные и операция деления (хп+1)/Р(х) используется в основе построения алгоритмов декодирования;;
7. Двучлен ЦК вида хп-1 можно разложить на множители
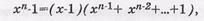
Пример:. Разложить двучлен хп-1=х7-1 на множители.
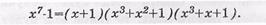 |
Двучлен х7-1 раскладывается на следующие многочлены:
Из данного выражения видно, что можно образовать шесть делителей для двучлена х7-1, путем комбинирования полученных трех сомножителей. Следовательно, для двучлена x7-1 существует шесть разных двоичных линейных ЦК со следующими образующими полиномами и параметрами:
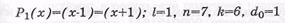 – простой код: l, k, n и tисп (tисп -кратность исправленных ошибок) - измеряются в двоичных символах;
– простой код: l, k, n и tисп (tисп -кратность исправленных ошибок) - измеряются в двоичных символах;
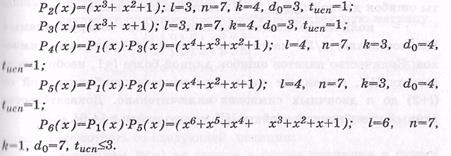
ЦК, задаваемые образующими полиномами Р1(х), P2(x) и Р3(х), относятся к классу ЦК Хэмминга. ЦК, задаваемые полиномами Р4(х), P5(x) и Р6(х), являются двойственными кодами Хэмминга и называются кодами максимальной длины.
Корректирующая способность групповых СЛБК зависит от вида (структуры) образующего полинома, т.е. от количества ненулевых членов данного полинома и его максимальной степени l=n-k. В соответствии с этим можно отметить следующие свойства ЦК:
а) обнаруживающих ошибки:
- ЦК, образующий полином которого имеет более одного члена и не имеет общего множителя х, обнаруживает все одиночные ошибки и любое нечетное число ошибок. Простейшим образующим полиномом ЦК, обладающими данными свойствами, является полином вида Р(х)=1+х;
- ЦК, образующий полином которого имеет вид р(х)=1+хс, обнаруживает любое нечетное число ошибок. Доказательство этого утверждения становится ясным, если образующий полином представить в следующем виде
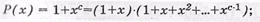
б) обнаруживающих и корректирующих ошибки: в виду того, что полином Р(х)=1+хс нацело делится на 1+х, то согласно предыдущему свойству ЦК обеспечивает обнаружение любого нечетного количества ошибок;
- ЦК, образующий полином которого имеет максимальную степень l=п-к, обнаруживает любой пакет ошибок длиной 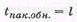 и менее двоичных символов или корректирует пакеты ошибок длиной
и менее двоичных символов или корректирует пакеты ошибок длиной 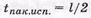 двоичных символов;
двоичных символов;
- количество пакетов длиной l+1, не обнаруживаемых ЦК, составляет 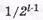 части всех пакетов (l+1) двоичных символов.
части всех пакетов (l+1) двоичных символов.
Количество пакетов ошибок длиной более l+1, необнаруживаемых ЦК, составляет часть всех пакетов ошибок длиной от (l+2) до n двоичных символов включительно.
Дата добавления: 2019-04-03; просмотров: 400;
