Способ формирования кодовых последователь­ностей циклического кода с использованием образующего полинома

Данный способ формирования кодовых последовательно­стей ЦК находит широкое применение на практике в виду его существенной простоты. При построении ЦК с использованием образующего полинома Р(х) могут быть сформированы кодовые последовательности как систематических, так и несистематиче­ских кодов.

При формировании кодовых последовательностей несисте­матического ЦК необходимо выполнить умножение передавае­мого информационного блока Q(x) степени (k-1) на порождающий полином P(x) с приведением по модулю два коэффициентов при слагаемых с одинаковыми показателями степеней. Таким образом, F_i(x)=Q(x)*P(x).

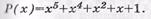Пример:Сформировать кодовую последовательность несистематического ЦК с параметрами 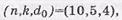если

Решение:

1) выбираем информационный блок Q(x) следующего вида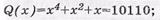

2) формируем кодовую последовательность по правилу

F(x)=Q(x)*P(x)=(x⁴+x²+x)(x⁵+x⁴+x²+x+1)= x⁹+x⁸+x⁷+x⁶+x (1111000010)

В данной кодовой последовательности нет четкого деления на блоки информационных и проверочных символов.

Сущность построения систематического ЦК с использова­нием образующего полинома состоит в следующем:

1) передаваемый информационный блок из k двоичных символов представляется многочленом Q(x) степени (k-l);

2) многочлен Q(x) умножается на член Р(х) с макси­мальной степенью x^l=x^n-k, т.е. Q(x)×x^l, что эквивалентно припи­сыванию к Q(x) со стороны младших разрядов l=n-k нулевых двоичных символов (разрядов);

3) выполняется деление произведения Q(x)×x^l на образующий полином Р(х) до получения остатка R(х) со степенью меньшей максимальной степени образующего полинома Р(х). Данный остаток R(х) представляет собой сформированные проверочные символы;

4) дописать остаток R(х) к произведению Q(x)*x^l. Следовательно, процесс формирования кодовой последовательности ЦК c использованием образующего полинома можно записать так:

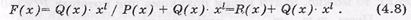
Пример:. Сформировать кодовую последовательность систематического ЦК с параметрами (n,k,do) – (13,8,5).

Решение:

а) так как k=8, то выбираем информационный многочлен 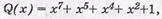а максимальную степень образующего по­линома принимаем равной l=n-k=13-8 =5. Выбираем табулирован­ный образующий, полином вида Р(х)=х⁵+х³+1;

б) далее в соответствии с вышерассмотренными операциями получаем:

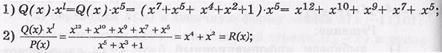
в) следовательно,

F(x) = Q(x)×x^l +R(x) = х¹²+ х¹⁰+ х⁹+ х⁷+ х⁵+ х⁴+ х² = 1011010110100.