Пример: полосовой фильтр

В качестве другого примера рассмотрим полосовой фильтр (т.е. фильтр, хорошо пропускающий сигналы на частоте внутри заданной полосы и отсекающий сигналы других частот) – на рис. 2.31 приведена схема. Нетрудно видеть, что эта схема отличается от схемы на рис. 2.27 лишь тем, что выходное напряжение снимается с конденсатора (а не со всего контура). Опять примем, что выполнено неравенство ρ >> 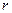. Записываем коэффициент передачи:

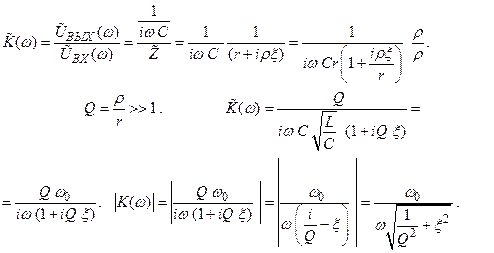
(2.59)

Выберем Тогда

(2.60)

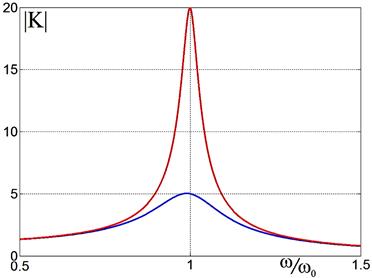
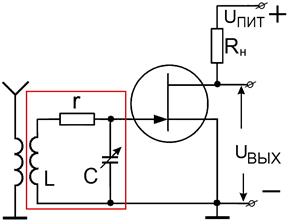
Рис. 2.31. Рис. 2.32.

Пример полосового фильтра в Резонансные кривые полосового фильтра

радиоприёмном устройстве. для двух значений добротности Q = 5 и 20.

На резонансе (ω = ω₀ ) имеем: | K(ω₀)| = Q >> 1 .

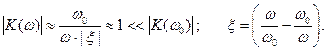
Вдали от резонанса: ω << ω₀ ,

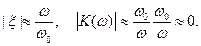
ω >> ω₀ ,

ширина полосы фильтра:

Это видно и на графике рис. 2.32.

Цепочка Вина

Цепочка Вина с равными сопротивлениями и ёмкостями (симметричная) попала в один раздел с LC-контурами потому, что частотная характеристика цепочки имеет максимум.

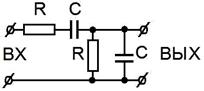
Рис. 2.33.

Схема цепочки Вина (Max Carl Wien).

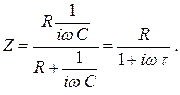
Импеданс параллельной RC цепочки будет: Здесь τ = RC.

Коэффициент передачи будет:

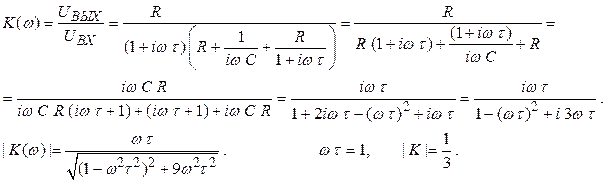
(2.61)

При (2.62)

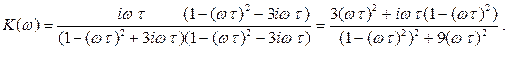Фазовую характеристику можно получить из (2.61), выделив вещественную и мнимую части.

(2.61')

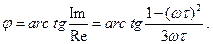
Отсюда: (2.63)

Графики частотной характеристики приведены ниже. При ωτ = 1 ЧХ достигает максимума, и на этой частоте сдвиг фаз φ между входным и выходным напряжениями равен нулю.

Эти свойства используются в генераторах низкой частоты. Современная схема происходит из работы Уильяма Хьюлетта на степень магистра в 1939 г. в Стэнфордском университете. Хьюлетт с Дэвидом Паккардом основали фирму Хьюлетт-Паккард. Их первой продукцией был прецизионный синусоидальный генератор HP200A, основанный на мосте Вина.

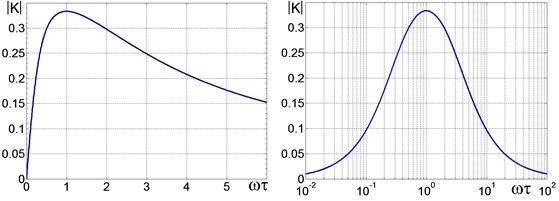
Рис. 2.34. Рис. 2.35.

ЧХ симметричной цепочки Вина с линейной и логарифмической шкалой частот.