Пример – фильтр-пробка

Часто используют резонансные свойства контура для различных фильтрующих устройств, например как показано на рис. 2.27.

При условии ρ >> R_i >> r схема на рис. 2.27 будет работать как фильтр-пробка, то есть сильно ослаблять переменное напряжение в полосе частот вблизи резонансной частоты, а напряжение вне полосы пропускать.

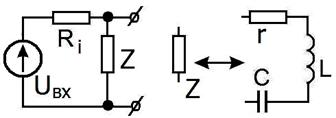
Рис. 2.27.

Схема фильтра-пробки.

Рассчитаем коэффициент передачи такой цепи:

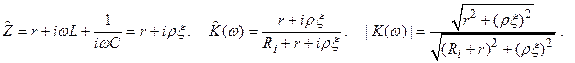Если R_i >> | 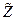(ω)|, то 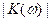→ 0. Если R_i <<| 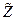(ω)|, то 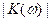→ 1.

(2.56)

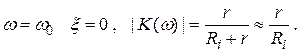
При

При

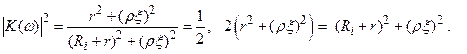
Вычислим частоты, на которых модуль коэффициента передачи уменьшается до уровня 0.7.

Так как R_i >> r , то: 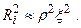(2.57)

Корень извлекать нельзя, так как расстройка бывает отрицательной (см. рис. 2.28).

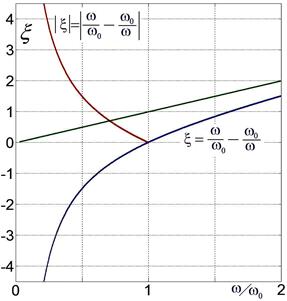
Рис. 2.28.

График зависимости расстройки ξ от круговой частоты ω.

Зелёная прямая линия – асимптота для больших частот.

Красная линия – график |ξ(ω)| .

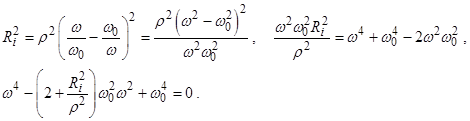
Здесь

(2.58)

2Δω – это ширина резонансной кривой на уровне 0.7, а Q_NEW – новая добротность – только для этой схемы.

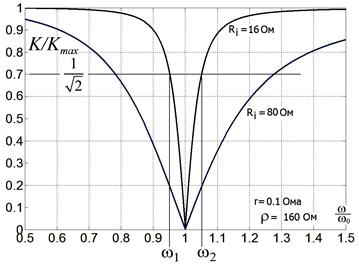
Рис. 2.29.

Зависимость нормализованного коэффициента передачи
фильтра-пробки от частоты по формуле (2.56).

Показана ширина полосы частот на уровне 0.7 для контура с добротностью Q_NEW = ρ/R_i = 10.

ρ >> R_i >> r ,

160 Ом >> 16 Ом >> 0.1 Ома.

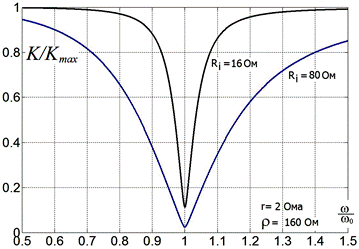
Рис. 2.30.

Те же зависимости для бόльшего сопротивления катушки индуктивности r = 2 Ома.