Где u и v – функции переменной интегрирования, например х.
Правила интегрирования
1) Для получения неопределённого интеграла от данной функции ƒ(х)необходимо найти одну из её первообразных и прибавить к ней произвольную постоянную.
2) Для проверки правильности полученного результата необходимо помнить, что производная от результата интегрирования должна равняться подынтегральной функции.
Основные свойства неопределённого интеграла
Свойство1. Производная от неопределённого интеграла равна подынтегральной функции, а дифференциал – подынтегральному выражению:
( ∫ ƒ(х)dx )' = ƒ(х) ; d ∫ ƒ(х)dx = ƒ(х)dx.
Свойство 2. Неопределённый интеграл от производной (дифференциала) функции равен этой функции, сложенной с произвольной постоянной:
∫ F'(х)dx = F'(х) + с или ∫ dF(x) =F(x)+ с.
Свойство 3. Постоянный множитель можно выносить за знак интеграла:
∫ af(x)dx = a∫ f(x)dx, где а = соnst, а ≠ 0.
Свойство 4. Неопределённый интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов:
∫ (ƒ(x)+y(x) –g(x))dx = ∫ ƒ(x)dx + ∫ y(x)dx – ∫ g(x )dx.
Геометрический смысл неопределённого интеграла
Неопределённый интеграл в системе Оху представляет семейство плоских кривых, смещенных друг относительно друга вдоль оси Оу.
Основные формулы интегрирования

Методы интегрирования
Непосредственное интегрирование
Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.
Например,
∫ (4х³ − 15х² +14х−3 )dx = ∫ 4x³dx − ∫ 15x²dx + ∫ 14xdx − ∫ 3dx = 4 x4 /4 − 15 x³/3 + 14 x²/2 − 3x + c = = x4 − 5x³ + 7x ²− 3x + C;
∫(х2+1)2dx=∫(х4+2х2+1)dx=∫х4dx+2∫x2dx+∫dx=x5/5+2x3/3+x+C;
 .
.
Интегрирование способом подстановки
При интегрировании подстановкой вводится новая переменная с таким расчётом, чтобы получить один из табличных интегралов. Найдя интеграл по новой переменной, надо возвратиться к первоначальной переменной и дать окончательный ответ.
Указать общее правило для выбора подстановки нельзя, так как этот выбор в каждом отдельном случае зависит от вида подынтегральной функции.
Например, найти следующие интегралы:
1 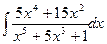 .
.
Решение. Применим подстановку 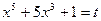 , где t – новое переменное. Продифференцируем обе части равенства:
, где t – новое переменное. Продифференцируем обе части равенства:
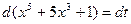 или
или  .
.
Теперь можно записать
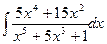 =
= 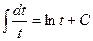 .
.
Возвращаясь к первоначальной переменной, получим окончательно:
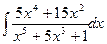 =
= 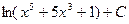
Приступая к интегрированию рациональных функций, следует посмотреть, нельзя ли подынтегральную функцию привести к такому виду, чтобы в числителе была производная от знаменателя, тогда можно будет сразу записать ответ.
2  .
.
Решение. Находим производную знаменателя: 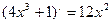 . Сравнивая это выражение с числителем, замечаем, что там нет сомножителя 12. Если умножить числитель дроби на 12, а за знак интеграла вынести сомножитель 1/12, то получим:
. Сравнивая это выражение с числителем, замечаем, что там нет сомножителя 12. Если умножить числитель дроби на 12, а за знак интеграла вынести сомножитель 1/12, то получим:
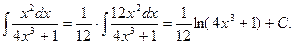
3 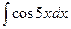
Решение. Полагаем 5х=t, тогда 5dx=dt и dx=1/5dt;
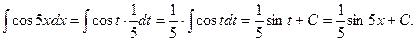
4 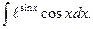
Решение. Положим sinx=t, тогда cosxdx=dt;
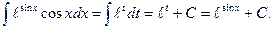
Интегрирование по частям
Интегрирование по частям производится по формуле:
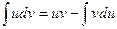 ,
,
Где u и v – функции переменной интегрирования, например х.
Пользуясь формулой интегрирования по частям, необходимо соблюдать требование, чтобы dx обязательно входило в состав dv и чтобы через dv была обозначена такая функция, интеграл которой можно легко найти.
Например,
.
Решение. Положим u=lnx, dv= x2dx, откуда (дифференцируя u и интегрируя dv)
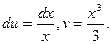
Постоянная С в этом случае не ставится; она будет поставлена в окончательном результате, когда будет найден данный интеграл.
Обращаемся теперь к формуле интегрирования по частям:
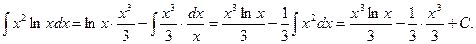
Дата добавления: 2017-12-05; просмотров: 1300;
