Параллельный контур
Рассмотрим параллельный колебательный контур, возбуждаемый гармоническим генератором тока, то есть таким генератором, ток которого не зависит от сопротивления внешней цепи (рис. 2.36). Опять будем рассматривать только случай установившихся колебаний. Выражение для комплексной проводимости параллельного контура можно найти, если сложить проводимости индуктивности, ёмкости и сопротивления.
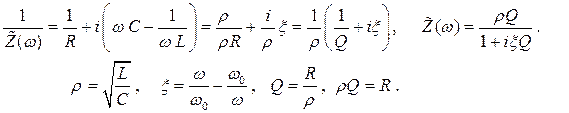
(2.64)
Здесь
Расстройку ξ мы ввели при выводе формулы (2.40), а добротность Q для данной схемы параллельного контура определена не так, как у последовательного.
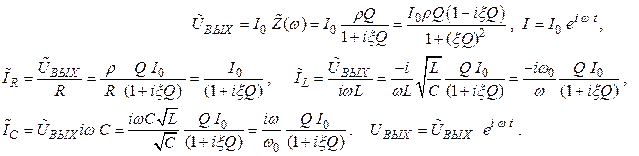 Выходное напряжение: (2.65)
Выходное напряжение: (2.65)
 Заметно, что IC = – IL при ω = ω0 или ξ = 0, ток от генератора течёт только через сопротивление R и токи через индуктивность и ёмкость в Q-раз больше. Токи равны и противофазны! При этом, конечно, сопротивление контура равно R и говорят, что оно чисто омическое.
Заметно, что IC = – IL при ω = ω0 или ξ = 0, ток от генератора течёт только через сопротивление R и токи через индуктивность и ёмкость в Q-раз больше. Токи равны и противофазны! При этом, конечно, сопротивление контура равно R и говорят, что оно чисто омическое.
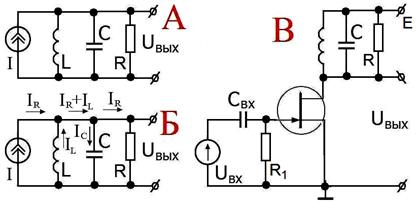
Рис. 2.36.
А – параллельный колебательный контур.
Б– токи в цепи на резонансе.
В – пример использования параллельного контура в цепи стока резонансного усилителя на полевом транзисторе.
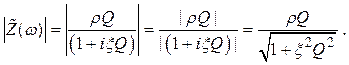 Частотная характеристика резонансного усилителя, показанного на схеме рис. 2.36 В, определяется частотной зависимостью модуля импеданса контура. Из (2.64) мы можем получить эту зависимость:
Частотная характеристика резонансного усилителя, показанного на схеме рис. 2.36 В, определяется частотной зависимостью модуля импеданса контура. Из (2.64) мы можем получить эту зависимость:
(2.66)
При ξ =0 модуль импеданса равен ρQ = R.
На рис. 2.37 показан график зависимости обезразмеренного импеданса |Z̃ /ρ| от частоты. Он имеет максимум на резонансной частоте, равный значению добротности Q.
Значение частот, при которых 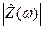 равен 0.7 от максимального можно найти из (2.66).
равен 0.7 от максимального можно найти из (2.66).
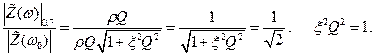
Такое уравнение мы уже решали
(см. (2.57), (2.58)).
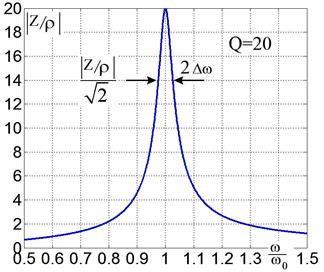
Рис. 2.37.
Зависимость безразмерного модуля импеданса параллельного контура от частоты.
На уровне 0.7 получаем условие ξ2 Q2 = 1.
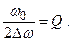
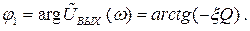 Из (2.65):
Из (2.65):
Напряжение на выходе сдвинуто по фазе относительно тока генератора. Формула для фазы получается такая же, как и (2.45) а, значит, и график будет такой же. Поэтому, посмотрите график на рис. 2.23.
И векторная диаграмма токов на резонансе будет похожа на рис. 2.21. Токи в катушке индуктивности L и в конденсаторе C будут равны и противофазны! И вдвоём не будут потреблять энергию от источника питания, который будет работать только на нагрев резистора R.
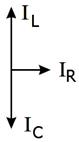
Рис. 2.38.
Векторная диаграмма токов на резонансе.
Для предельных случаев большой и малой добротностей получаем для уровня 0.7 ξ2 Q2 =1.
Решая это биквадратное уравнение для Q << 1, нужно при извлечении корня опять удерживать и линейный и квадратичный члены разложения бинома Ньютона.
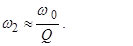
При Q << 1 ω1 ≈ Q ω0 ,
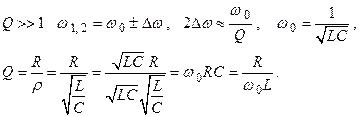
При
(2.67)
Заметим, что для нашего параллельного контура определение добротности Q отличается от определения добротности для последовательного контура.
В последовательном – чем меньше сопротивление, тем выше добротность. См. (2.40).
В параллельном – чем больше сопротивление, тем выше добротность. См. (2.67). Это вполне логично.
Добротность
Понятие добротности является важнейшей характеристикой резонаторов. Во многих приборах максимальная величина добротности является ключевым параметром.
Приведём различные определения добротности Q:

Запасённая энергия Это из (2.49).
( Потеря энергии за период )
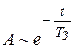 Введём новую константу TЗ – время затухания в контуре, в котором амплитуда
Введём новую константу TЗ – время затухания в контуре, в котором амплитуда
свободных колебаний уменьшается по закону (см. (2.36)).
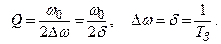
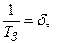
Тогда из (2.36) а из (2.41 и 2.55)
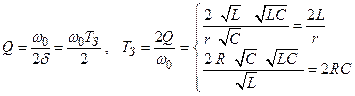
(последовательный контур),
(параллельный контур).
Свободные колебания в контуре затухают по закону e–δt . Если t = QT, то
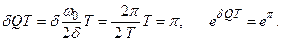
Итак, при свободных колебаниях амплитуда уменьшается в eπ раз, то есть в 23 раза за
Q периодов. Посмотрите на колебания в контуре с добротностью Q = 5 на рис. 2.20. Пятый максимум как раз в 23 раза меньше первого. Проверьте! Это ещё один замечательный способ представить себе, что такое добротность.
Таблица. Примеры добротностей различных резонаторов.
| Вид резонатора | Добротность | Частотный диапазон |
| Обычный LC контур при комнатной температуре | Q ≈ 50…300 | f ≈105…108 Гц |
| СВЧ резонатор при комнатной температуре | Q ≈ 50…105 | f ≈ 109…1012 Гц |
| Сверхпроводящий СВЧ резонатор при гелиевой температуре ~ 4K | Q ≈ 106…1010 | f ≈ 109…1012 Гц |
Мкостный датчик
Ёмкостный датчик является прибором для высокоточных измерений механических смещений. Принцип его работы следующий. Генератор гармонических колебаний настраивается на склон резонансной частоты контура, как показано на рис. 2.40. Тогда изменение расстояния d между пластинами конденсатора (которое и измеряется) на величину Δd приведёт к изменению собственной частоты контура, а, следовательно, к сдвигу резонансной кривой. Это в свою очередь приведёт к изменению напряжения UС на конденсаторе на величину ΔUC , которое и измеряется. Можно показать, что при определённых условиях связь между ΔUC и Δd имеет вид
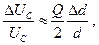
где Q — добротность контура. Чтобы оценить, какую величину Δd можно измерить, зададим следующие параметры:
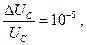
Q = 200, d = 0.1 мм. Тогда Δd =0.01 нм = 0.1 Å.
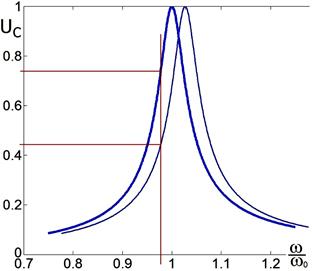
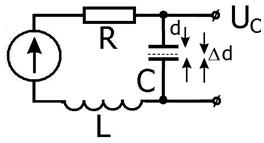
Рис. 2.39.
Схема простого ёмкостного датчика.
Настоящие схемы много сложнее.
Рис. 2.40.
При увеличении расстояния между пластинами конденсатора его ёмкость уменьшается. Резонансная кривая сдвигается в область бо́льших частот. Если частота генератора постоянна, то выходное напряжение в нашей ситуации падает.
Связанные контуры
Рассмотрим два связанных контура, изображённых на рис. 2.41. Пусть на вход первого действует гармоническое напряжение UBX (t)=Ũ0 eiωt и нас интересует, каково будет напряжение на выходе UВЫХ (t) = Ṽ0 eiωt. Опять рассматриваем случай установившихся колебаний. Тогда для токов I1 и I2 в каждом контуре получаем систему двух уравнений:
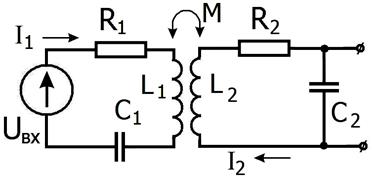
Рис. 2.41.
Схема двух связанных контуров.
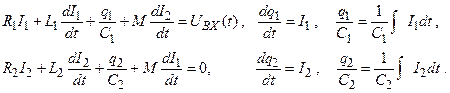
(2.68)
(2.69)
Здесь М – коэффициент взаимоиндукции.

Ищем токи в виде
где Ĩ1 , Ĩ2 – комплексные амплитуды. Подставляя их в систему (2.68, 2.69) получаем:
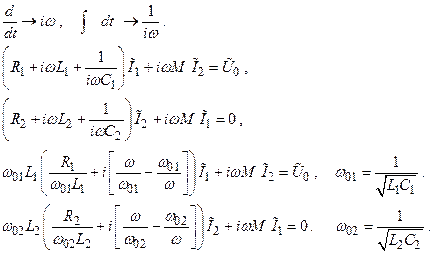
или
(2.70)
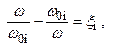
(2.71)
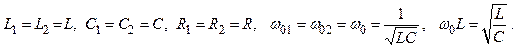 Эта система может быть решена. Для простоты рассмотрим более подробно простейший случай, когда контуры одинаковы:
Эта система может быть решена. Для простоты рассмотрим более подробно простейший случай, когда контуры одинаковы:
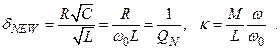
Обозначим:
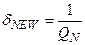
Заметьте, что здесь – безразмерное.
Тогда разделив оба уравнения (2.70, 2.71) на 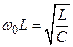 , можно их переписать в виде:
, можно их переписать в виде:
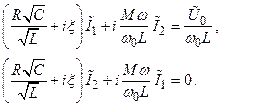
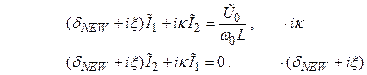
Получим: (2.72)
(2.73)
Исключим Ĩ1 . В результате получим решение для Ĩ2 , через которое можно выразить комплексную амплитуду Ṽ0 выходного напряжения и коэффициент передачи K̃ :
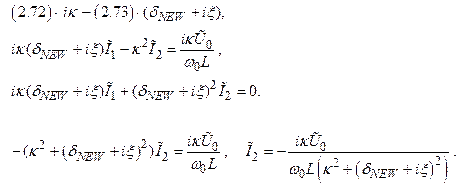
Вычтем и получим:
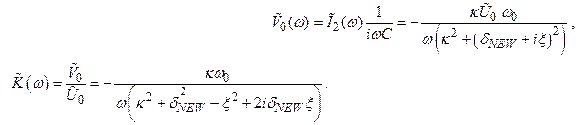
Напряжение на конденсаторе будет (2.74)
(2.75)
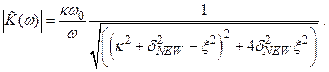
(2.76)
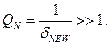
Рассмотрим случай большой добротности, т.е.
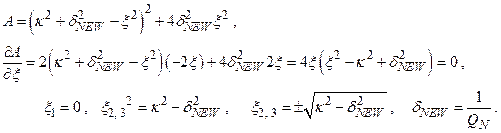 При большой добротности нас будут интересовать только малые расстройки ξ << 1. Поэтому, мы можем считать, что κ ≈ const. Чтобы оценить форму резонансной кривой будем искать экстремумы квадрата модуля знаменателя (2.76) по переменной ξ :
При большой добротности нас будут интересовать только малые расстройки ξ << 1. Поэтому, мы можем считать, что κ ≈ const. Чтобы оценить форму резонансной кривой будем искать экстремумы квадрата модуля знаменателя (2.76) по переменной ξ :
(2.77)
Корни (2.77): (2.78)
Отсюда сразу видно, что при κ < δNEW коэффициент передачи K̃(ω) имеет один экстремум, а при κ > δNEW — три экстремума. Два максимума и один минимум.

Рис. 2.42.
Резонансные кривые связанных контуров (2.76). QN = 100.
При увеличении связи между контурами резонансные кривые становятся двугорбыми.
Буквой П помечены кривые, более всего похожие на эту букву.
Использование комбинации нескольких контуров позволяет сделать почти идеальный
П-образный полосовой фильтр. Ширина полосы и крутизна фронтов зависит от числа и параметров использованных контуров.
Для любознательных. Не для экзамена.Программа для MATLAB. Вычисляет и строит кривые рис.2.42.
clear all; clc; % Рис.2.46. Связанные контура
FigureColor=[1,1,1]; hFigure=gcf; set(hFigure, 'Color', FigureColor)
for M =0.002: 0.002: 0.022 %Разные коэффициенты связи
del=.01; %Дельта
w=[0.96:.0001:1.04]; %Омега
kap=M./w; %Каппа
ksi=(w.*w-1)./w; %Кси
K=M./sqrt((kap.*kap+del.*del-ksi.*ksi).*(kap.*kap+del.*del-ksi.*ksi)+4.*del.*del.*ksi.*ksi);
%Модуль коэффициента передачи
plot(w+4*M,K-M*2500,'b-', 'LineWidth',3); hold on; %grid on;
end
Трансформатор
В электротехнике трансформатор (рис. 2.43) представляет собой устройство для увеличения или уменьшения переменного напряжения. В радиоэлектронике он ещё используется и для согласования нагрузок, а также для разделения цепей питания. Рассмотрим его работу подробнее. Опять записываем входное напряжение генератора синусоидального напряжения в комплексной форме UВХ (t) = U1 eiωt , а токи в каждом контуре в виде I1 = i1 eiωt , I2 = i2 eiωt . Тогда, записывая правило Кирхгофа в каждом контуре, получим систему:

(2.79)
(2.80)

Рис. 2.43.
Схема идеального трансформатора.
Здесь мы для дальнейшего удобства выбрали знак (–) перед коэффициентом взаимоиндукции М. Обычно в электротехнических приборах для работы трансформатора должны быть выполнены три условия:
1. Коэффициент взаимоиндукции М максимален, т.е. М 2 ≈ L1 L2.
2. Индуктивное сопротивление в первом контуре значительно больше активного, т.е. R1 << ω L1.
3. То же самое для второго контура: R2 << ω L2.
Используя эти условия, и вводя обозначение 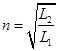 , получаем из уравнения (2.80):
, получаем из уравнения (2.80):


Величина n называется коэффициентом трансформации (это название понятно из последнего равенства). Индуктивность пропорциональна квадрату числа витков для идеального трансформатора с полностью общим магнитным потоком. Потерями магнитного потока пренебрегаем.
Отношение числа витков – это коэффициент трансформации: w2/w1 = n. Если трансформатор повышает напряжение, то ток во вторичной обмотке уменьшается.
Решаем систему (2.79, 2.80), учитывая условия работы трансформатора.

Из (2.80)




 (2.81)
(2.81)

(2.82)

 (2.83)
(2.83)
Из выражений (2.82, 2.83) следует, что трансформатор на рис. 2.43 может быть представлен двумя эквивалентными схемами, изображёнными на рис. 2.44.
Можно сказать, что схема А “приведена к выходу” – она показывает, какой эквивалентный генератор действует во вторичной цепи с сопротивлением R2.
Тогда схему Б можно назвать “приведённой ко входу” – по ней видно, как сопротивление R2 пересчитывается в эквивалентное сопротивление в первичной цепи генератора U1.

Рис. 2.44.
Две
эквивалентные
схемы
трансформатора.
Из (2.83) и схемы Амы можем рассчитать напряжение U2 = i2 R2 на нагрузке во вторичной цепи и вычислить коэффициент передачи напряжения K:
 при (2.84)
при (2.84)
Мы видим, что коэффициент передачи равен коэффициенту трансформации (K ~ n) лишь при достаточно малом сопротивлении в первичной цепи, т.е. при R2 >> n2 R1 , и полностью совпадает лишь при разомкнутой внешней цепи, то есть в режиме холостого хода.
В заключение выпишем выражения для мощности во вторичной цепи, соответствующие двум эквивалентным схемам:

– схема А , –схемаБ. (2.85)
Они одинаковы. Мощность здесь поделена на 2 потому, что ток синусоидальный. А эффективное значение синусоидального тока равно 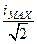 .
.
Трансформаторы часто применяются для согласования источника сигнала с нагрузкой. Действительно, в простейшей схеме с источником напряжения, внутреннее сопротивление которого равно Ri, передаваемая в нагрузку мощность зависит от сопротивления нагрузки RH. Если сопротивление нагрузки равно нулю, то на ней нет напряжения и мощность тоже равна нулю. Если сопротивление нагрузки стремится к бесконечности, то ток стремится к нулю, а вместе с ним и мощность.
 Где находится максимум передаваемой мощности?
Где находится максимум передаваемой мощности?
Рис. 2.45.
Согласование с нагрузкой.

Максимум при
По схеме А: то есть . (2.86)
Дата добавления: 2019-04-03; просмотров: 742;
