Условие дифференцируемости на частотном языке

Давайте рассмотрим, при каких условиях цепочки, изображённые на рис. 2.14, будут приближённо дифференцирующими для гармонического (синусоидального) сигнала.

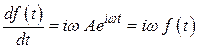
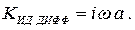Из (2.10) . Значит, коэффициент передачи идеальной

дифференцирующей цепочки должен быть (2.23)

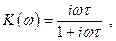
Коэффициент передачи этих цепочек будет: (2.24)

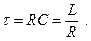
где постоянные времени этих цепочек:

Из (2.24) виден ещё один признак хорошего дифференцирования: ωτ должно быть много меньше единицы, а постоянная времени цепочки должна быть много меньше периода

синусоиды T: то есть частота (2.25)

При этом условии в знаменателе (2.24) останется только единица, а коэффициент передачи будет |K(ω)| << 1.

Обратим сразу внимание, что две цепочки, составленные из разных элементов, обладают подобными характеристиками. Более того, эти цепочки становятся идентичными при RC = L/ R.

Это означает, что на выходе наших цепочек мы получим производную от входного сигнала, если частоты будут достаточно низкими, ω << 1/τ . Естественно, мы получим производную в некотором приближении, и это приближение будет тем лучше, чем лучше выполняется неравенство (2.25).