Импульсная характеристика

Важную роль в радиоэлектронике играет так называемая δ-функция. Входное напряжение можно разложить по этим δ-функциям. Сама δ-функция узка, но высока настолько, что интеграл от неё всегда равен единице. В радиоэлектронике ею моделируют очень короткие импульсы. Ниже об этом будет рассказано немного подробнее. Пока поверьте, что 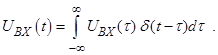Это – фактически определение δ-функции.

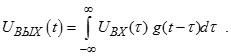Тогда выходное напряжение может быть представлено в виде суперпозиции по некоторым функциям g(t).

(2.13)

Физический смысл импульсной характеристики g(t) заключается в том, что она описывает реакцию линейной системы на дельта-функцию δ (t).

Поэтому, зная импульсную функцию g(t), можно рассчитывать выходное напряжение по формуле (2.13), подставляя входное напряжение.

Переходная характеристика h(t)

Иногда частотный способ описания не так удобен, как временно́й.

Введём ступенчатую функцию Хевисайда H(t), определяемую как

если

если

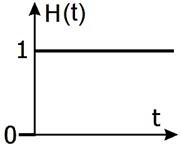
Рис. 2.9.

Единичная функция или функция Хевисайда.

Или просто ступенька.

Введём переходную характеристику h(t) как реакцию линейной системы на ступеньку H(t). Реакция – это зависимость выходного напряжения от времени. Примеры применения переходных характеристик будут рассмотрены ниже.

Интеграл Дюамеля

Произвольный входной электрический сигнал можно представить в виде суммы ступенек небольшой амплитуды, как это показано на рис. 2.10.

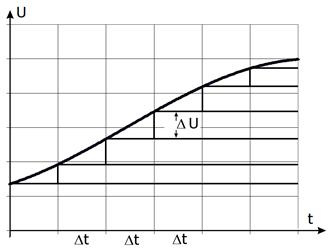
Рис. 2.10. Представление сигнала произвольной формы в виде суммы большого числа сдвинутых по времени на Δt ступенек.

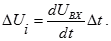
Если скачки ΔU маленькие, то их можно записать как

Тогда из рис. 2.10 видно, что U_ВХ (t) можно представить как

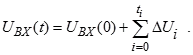
Если устремить Δt к нулю, то можно сумму заменить интегралом.

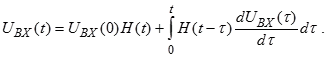
(2.14)

Это и есть интеграл Дюамеля (Duhamel).

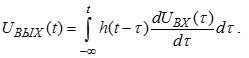Тогда выходное напряжение линейной системы при произвольном воздействии может быть представлено в виде суперпозиции по функциям h(t), то есть по откликам системы на ступеньку.

(2.15)

Конечно, всё это работает только в линейных цепях, в которых действует принцип суперпозиции.