Уравнение неразрывности
Применительно к некоторой массе жидкости или газа, занимающего произвольно выделенный объем, закон сохранения массы можно сформулировать в следующем виде: масса жидкости или газа, состоящая из одних и тех же частиц, в процессе движения остается постоянной.
Естественно предполагается, что скорости движения жидких частиц значительно меньше скорости света, а это позволяет пренебречь релятивистскими эффектами изменения массы.
Движение жидких частиц будем рассматривать в трехмерном ортогональном пространстве с декартовыми координатами 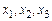 и единичными ортами
и единичными ортами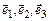 .Слово «ортогональность» означает взаимную перпендикулярность координатных осей.
.Слово «ортогональность» означает взаимную перпендикулярность координатных осей.
Используем часто применяемые в современной физической и математической литературе правила, позволяющие упростить запись: каждый буквенный индекс, встречающийся в выражении один раз, может принимать значения 1, 2, 3.
При этом, поскольку для обозначения координатных осей выбраны буквы с индексами (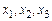 ), под записью
), под записью 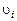 , например, будем понимать совокупность трех проекций скорости
, например, будем понимать совокупность трех проекций скорости 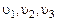 ; запись
; запись 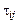 означает совокупность
означает совокупность 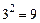 величин:
величин: 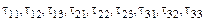 .
.
По дважды повторяющемуся в одночлене индексу (за немногими, всегда оговариваемыми случаями) следует производить суммирование от 1 до 3.
Таким образом, выражения 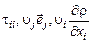 означают:
означают:
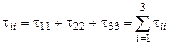 ,
,
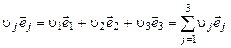 , (2.1.1)
, (2.1.1)
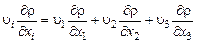 .
.
Индексы суммирования часто называются «немыми» в том смысле, что сумма, очевидно, не меняет значение, если заменить «немой» индекс другой буквой: 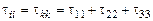 и т.д.
и т.д.
Во избежание путаницы в обозначениях индексы, относящиеся к химическому элементу или соединению, там, где это необходимо, будем для векторных и тензорных величин ставить вверху.
Так, например, выражение 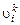 может обозначать проекцию скорости k-го химического компонента на ось
может обозначать проекцию скорости k-го химического компонента на ось 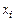 .
.
Скалярные величины, такие как плотность, температура, давление и т.д., поскольку они инвариантны по отношению к любому преобразованию координат, для химических соединений или элементов обозначаем, как и ранее, индексом внизу. Например, 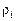 – плотность i-го компонента смеси.
– плотность i-го компонента смеси.
Приняв во внимание сделанные замечания, перейдем к математической записи закона сохранения массы для смеси газов.
Плотность смеси найдем по формуле
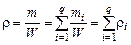 . (2.1.2)
. (2.1.2)
Скорость жидкой частицы 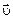 определим как среднемассовую скорость всех компонентов, составляющих смесь:
определим как среднемассовую скорость всех компонентов, составляющих смесь:
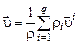 . (2.1.3)
. (2.1.3)
Масса газа, заключенная в объеме W и ограниченная замкнутой поверхностью S,равна:
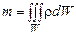 . (2.1.4)
. (2.1.4)
Будем считать, что внутри выделенного объема нет источников и стоков, через которые газ мог бы подаваться в заданный объем или извлекаться из него. Тогда масса газа, находившегося внутри объема W в момент времени t, в последующие моменты времени, в соответствии с законом сохранения массы, останется неизменной. Конечно при этом нужно учитывать смещение граничной поверхности S из-за движения граничных жидких частиц.
Итак, в момент времени t масса газа внутри объема W равна:
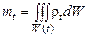 . (2.1.5)
. (2.1.5)
За промежуток времени 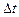 подынтегральная функция
подынтегральная функция 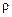 и объем W,занятый выделенными жидкими частицами, получили приращения:
и объем W,занятый выделенными жидкими частицами, получили приращения:
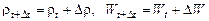 . (2.1.6)
. (2.1.6)
Подставляя соотношения (2.1.6) в (2.1.4), получим
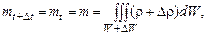
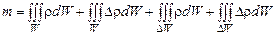 . (2.1.7)
. (2.1.7)
Изменение объема 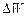 , связанное с перемещением за время
, связанное с перемещением за время 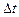 граничной поверхности, равно:
граничной поверхности, равно:
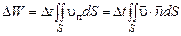 , (2.1.8)
, (2.1.8)
где 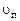 – проекция скорости граничных жидких частиц на внешнюю (направленную из объема) нормаль к поверхности S.
– проекция скорости граничных жидких частиц на внешнюю (направленную из объема) нормаль к поверхности S.
С учетом формулы (2.1.8) выражения для интегралов по объему 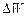 запишутся в виде
запишутся в виде
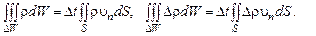 (2.1.9)
(2.1.9)
Так как масса газа m не меняется с течением времени, то полная производная по времени равна нулю:
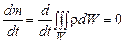 . (2.1.10)
. (2.1.10)
По определению производной,
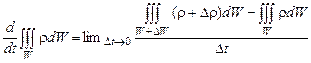 . (2.1.11)
. (2.1.11)
Подставляя в (2.1.11) зависимости (2.1.7) и (2.1.9) и переходя к пределу при 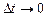 , получим интегральную форму записи закона сохранения массы:
, получим интегральную форму записи закона сохранения массы:
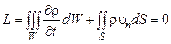 . (2.1.12)
. (2.1.12)
В частном случае установившегося движения, когда параметры газа в каждой фиксированной точке пространства не меняются с течением времени, интегральная форма уравнения неразрывности примет вид
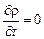 ;
; 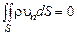 . (2.1.13)
. (2.1.13)
Для получения уравнения неразрывности в дифференциальной форме следует выбрать объем в виде прямоугольника с ребрами, параллельными координатным осям, разделить соотношение (2.1.12) на этот объем и перейти к пределу, стягивая объем в точку:
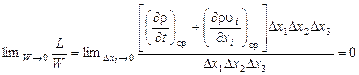 , (2.1.14)
, (2.1.14)
где 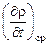 и
и 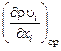 – средние по объему частные производные.
– средние по объему частные производные.
В результате получим уравнение неразрывности в дифференциальной форме в декартовой системе координат:
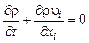 . (2.1.15)
. (2.1.15)
Напомним, что по повторяющемуся индексу i в формуле (2.1.15) производится суммирование от 1 до 3.
Если второе слагаемое в (2.1.15) представить в виде
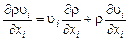 (2.1.16)
(2.1.16)
и учесть, что полная производная
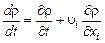 , (2.1.17)
, (2.1.17)
то (2.1.15) можно записать так:
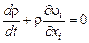 . (2.1.18)
. (2.1.18)
Для несжимаемой жидкости 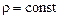 уравнение неразрывности примет вид
уравнение неразрывности примет вид
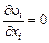 . (2.1.19)
. (2.1.19)
В литературе зависимость вида (2.1.19) называется дивергенцией вектора:
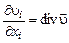 . (2.1.20)
. (2.1.20)
При использовании оператора Гамильтона, часто называемого также оператором набла 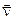 :
:
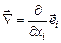 , (2.1.21)
, (2.1.21)
зависимость (2.1.19) можно записать в виде скалярного произведения:
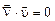 . (2.1.22)
. (2.1.22)
Заметим, что уравнение неразрывности для смеси газов записывается так же, как и для однокомпонентного газа, имеющего плотность и скорость, соответствующие смеси.
Уравнение движения
Второй фундаментальный закон, который мы используем, - закон изменения количества движения (импульса) некоторой системы материальных частиц: изменение вектора количества движения некоторой массы жидкости или газа, состоящей из одних и тех же жидких частиц, в единицу времени равно сумме всех внешних сил, действующих на выделенную массу жидкости или газа.
Количеством движения (импульсом) системы жидких частиц называется вектор 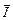 , равный сумме импульсов всех жидких частиц этой системы.
, равный сумме импульсов всех жидких частиц этой системы.
Выделим произвольный объем W с граничной поверхностью S. Каждая жидкая частица, находящаяся в этом объеме, обладает импульсом
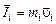 , (2.2.1)
, (2.2.1)
где 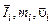 – соответственно количество движения, масса и скорость жидкой частицы. Выполнив интегрирование по объему W, получим количество движения системы:
– соответственно количество движения, масса и скорость жидкой частицы. Выполнив интегрирование по объему W, получим количество движения системы:
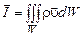 . (2.2.2)
. (2.2.2)
Производная от количества движения по времени равна:
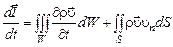 . (2.2.3)
. (2.2.3)
Промежуточные преобразования при выводе уравнения (2.2.3) опущены, так как они аналогичны соответствующим преобразованиям при выводе полной производной 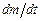 в подразд. 2.1.
в подразд. 2.1.
Внешние силы, действующие на выделенную массу газа m, складываются из массовых и поверхностных сил.
Массовые силы – это силы, которые приложены к каждому элементу массы и величина которых пропорциональна массе. Обозначим буквой 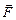 массовую силу, действующую на единицу массы. Тогда на всю массу газа, заключенную внутри объема W, будет действовать массовая сила, равная:
массовую силу, действующую на единицу массы. Тогда на всю массу газа, заключенную внутри объема W, будет действовать массовая сила, равная:
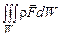 . (2.2.4)
. (2.2.4)
Поверхностные силы – это силы, которые воздействуют на граничную поверхность S,отделяющую выделенную массу жидкости или газа от окружающей среды.Они складываются из давления и трения.
Давление 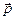 , действующее на единичную площадку с нормалью
, действующее на единичную площадку с нормалью 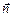 , равно:
, равно:
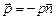 ; (2.2.5)
; (2.2.5)
знак «-» показывает, что давление направлено внутрь объема в сторону, противоположную нормали. Его величина не зависит от ориентации площадки.
Давление существует как в покоящейся, так и движущейся жидкости или газе. Суммарное давление на весь выделенный объем определяется как
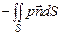 . (2.2.6)
. (2.2.6)
Трение зависит от скорости деформации жидкой частицы. Поэтому оно возникает только в движущейся и деформирующейся при движении жидкости или газе. Обозначим трение, действующее на единичную площадку с нормалью 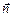 , через
, через 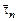 . Следует иметь в виду, что величина трения
. Следует иметь в виду, что величина трения 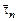 зависит от ориентации площадки, а его направление может не совпадать с направлением нормали. На всю поверхность S действует трение, равное:
зависит от ориентации площадки, а его направление может не совпадать с направлением нормали. На всю поверхность S действует трение, равное:
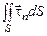 . (2.2.7)
. (2.2.7)
С учетом соотношений (2.2.3)–(2.2.7) уравнение, выражающее закон изменения вектора количества движения, запишем в интегральной форме:
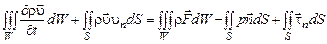 . (2.2.8)
. (2.2.8)
Получим интегральное соотношение для изобарической струи, истекающей в затопленное пространство или спутный поток. Спутный поток газа – это поток, скорость которого 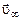 направлена параллельно оси.
направлена параллельно оси.
Сделаем такие допущения:
· массовые силы пренебрежимо малы;
· движение установившееся;
· в окружающей среде параметры постоянны;
· давление в струе постоянно и равно давлению в окружающей среде: 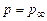 .
.
Выделим объем, заключенный между начальным сечением, проходящим через срез сопла, и любым другим сечением вниз по потоку. Применим закон изменения количества движения, используя значение избыточной скорости 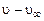 с тем, чтобы исключить из рассмотрения количество движения неизвестной нам массы газа, прошедшей через начальное сечение из окружающей среды.
с тем, чтобы исключить из рассмотрения количество движения неизвестной нам массы газа, прошедшей через начальное сечение из окружающей среды.
Из формулы (2.2.8) следует, что суммарное избыточное количество движения сохраняется по длине струи:
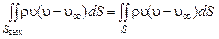 , (2.2.9)
, (2.2.9)
где 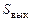 – площадь выходного сечения сопла,
– площадь выходного сечения сопла, 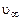 – скорость спутного потока.
– скорость спутного потока.
Если давление на срезе сопла 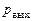 отличается от атмосферного, что возможно при сверхзвуковых скоростях истечения, то интегральный закон изменения количества движения на изобарическом участке струи примет вид
отличается от атмосферного, что возможно при сверхзвуковых скоростях истечения, то интегральный закон изменения количества движения на изобарическом участке струи примет вид
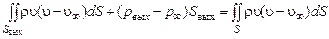 . (2.2.10)
. (2.2.10)
Для затопленной струи 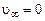 с учетом того, что реактивная сила R равна:
с учетом того, что реактивная сила R равна:

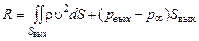 , (2.2.11)
, (2.2.11)
получим
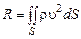 . (2.2.12)
. (2.2.12)
Если турбулентная струя формируется блоком, состоящим из нескольких сопл, то используется принцип сложения решений:
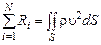 . (2.2.13)
. (2.2.13)
Для получения уравнения движения в дифференциальной форме в декартовой системе координат действуем по аналогии с выводом дифференциальной формы уравнения неразрывности:
· выбираем объем в виде прямоугольника с гранями параллельными координатным плоскостям;
· делим правую и левую часть уравнения (2.2.8) на этот объем;
· переходим к пределу, стягивая объем в точку.
Выполнив перечисленные выше операции, получим
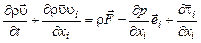 . (2.2.14)
. (2.2.14)
Левую часть уравнения (2.2.14) можно преобразовать следующим образом, используя уравнение неразрывности:
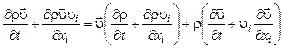 . (2.2.15)
. (2.2.15)
Так как в силу уравнения неразрывности
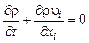 , (2.2.16)
, (2.2.16)
а полная производная от скорости по времени равна:
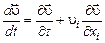 , (2.2.17)
, (2.2.17)
то (2.2.14) приводится к виду
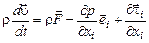 . (2.2.18)
. (2.2.18)
Силы трения, действующие на единичные площадки, перпендикулярные координатным осям, 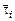 в проекциях на оси координат записываются в виде
в проекциях на оси координат записываются в виде
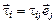 . (2.2.19)
. (2.2.19)
Совокупность девяти величин 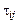 определяет аффинный ортогональный тензор второго ранга, который носит название тензора напряжений.
определяет аффинный ортогональный тензор второго ранга, который носит название тензора напряжений.
Дата добавления: 2018-11-25; просмотров: 1341;
