Определение равновесного состава и термодинамических характеристик смеси газов при заданных давлении и температуре

Определение состава и термодинамических характеристик равновесной смеси при заданных условной формуле смеси, давлении р и температуре T проводится при следующих основных допущениях:

· смесь реагирующих газов является равновесной;

· статическое давление смеси равняется, по закону Дальтона, сумме парциальных давлений газообразных компонентов;

· уравнение состояния для идеального газа справедливо как для отдельных газообразных компонентов, так и для смеси в целом;

· константы равновесия реакций зависят только от температуры;

· объем, занимаемый твердой фазой, пренебрежимо мал по сравнению с объемом, занимаемым газообразными продуктами;

· температуры твердой и газовой фаз равны. Парциальное давление газовой фазы равно давлению насыщенного пара для данного конденсированного химического соединения.

В соответствии с законом, установленным в 1840 г. русским академиком Г.Г. Гессом, тепловой эффект реакции не зависит от пути реакции при сохранении постоянными начальных и конечных условий. Это позволяет цепочку химических реакций, приводящих к образованию конечных компонентов, выбирать произвольно, исходя из удобства разработки алгоритма расчета.

В большинстве существующих программ термодинамических расчетов используется система реакций диссоциации конечных компонентов на атомы.

Тогда полная система уравнений для определения равновесного состава запишется в следующем виде.

Уравнение диссоциации всех ожидаемых молекулярных компонентов 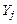на атомы :

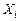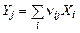, (1.6.1)

где 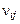– число атомов i-го химического элемента в компоненте j.

Закон действующих масс для неконденсированных веществ:

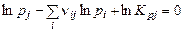, (1.6.2)

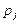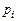где и – парциальные давления молекулярных и атомарных компонентов, а 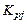– зависящая от температуры константа равновесия j-й реакции.

Закон действующих масс для газовой фазы конденсированных веществ:

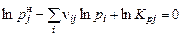, (1.6.3)

где 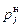– давление насыщенного пара для данного конденсированного химического соединения. При фиксированной температуре величины 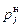известны.

Уравнения сохранения вещества, представляющие собой условия постоянства количества молей i-го химического элемента в процессе реакции:

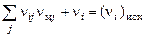, (1.6.4)

где 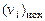– число молей i-го химического элемента в исходных продуктах, а 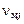и 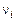– числа молей молекулярных и атомарных компонентов. По закону Авогадро моли различных идеальных газов при одинаковых условиях занимают одинаковый объем. Это позволяет связать 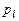и 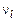соотношениями вида (см. (1.2.10) и (1.2.30)):

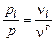, (1.6.5)

где 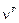– общее число молей газа, 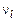– число молей l-го компонента газовой смеси, 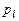– парциальное давление l-го компонента.

Закон Дальтона для газообразных компонентов:

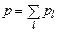. (1.6.6)

Общее количество молей конденсированного вещества 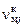складывается из числа молей в газовой 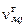и твердой 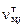фазах:

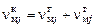. (1.6.7)

Аналогично для конденсированных элементов

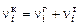. (1.6.8)

Число молей i-го химического элемента в исходных продуктах выражается через условную формулу смеси 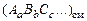и массу т в кг :

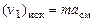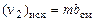, и т.д. (1.6.9)

Если обозначить через 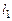– число газообразных веществ, 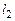– число газообразных элементов, 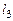– число конденсированных веществ, 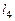– число конденсированных элементов, то можно написать 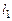уравнений (1.6.2), 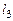– (1.6.3), 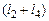– (1.6.4), 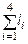– (1.6.5), 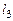– (1.6.7), 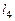– (1.6.8). В результате будем иметь замкнутую систему (1.6.2) – (1.6.9) для определения т, парциальных давлений газообразных продуктов и молярного состава смеси. Массовые доли выражаются через молярный состав (см. (1.2.11)):

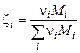. (1.6.10)

Если в смеси имеют место процессы ионизации, то система (1.6.2) – (1.6.9) дополняется уравнениями, выражающими закон действующих масс применительно к ионизации, которые формально могут быть записаны в форме (1.6.2), и условием сохранения заряда системы.

Система (1.6.2) – (1.6.9) решается численно методом последовательных приближений.

Рассмотренный выше порядок нахождения равновесного состава обладает универсальностью, так как введение нового химического соединения добавляет к системе (1.6.1) лишь одну реакцию диссоциации этого соединения на атомы. Однако для конкретных исходных веществ могут быть построены более простые и наглядные, но, естественно, менее универсальные схемы расчета равновесного состава.

В уравнениях, описывающих процесс развития турбулентной струи, применяются такие термодинамические величины: 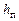– теплосодержание (энтальпия), R – газовая постоянная, 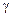– показатель адиабаты. Эти параметры определяются по соотношениям (1.2.40) – (1.2.46).