О вычислении констант равновесия
Константы равновесия 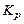 могут быть определены или расчетом по формуле (1.3.21), или опытным путем – по результатам замеров парциальных давлений газов, находящихся в состоянии химического равновесия (см. (1.3.20)).
могут быть определены или расчетом по формуле (1.3.21), или опытным путем – по результатам замеров парциальных давлений газов, находящихся в состоянии химического равновесия (см. (1.3.20)).
В ряде случаев удобно константы равновесия некоторых реакций вычислять по константам равновесия других реакций. Так, например, для реакций диссоциации углекислого газа:
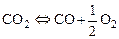 , (1.4.1)
, (1.4.1)
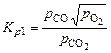 (1.4.2)
(1.4.2)
и диссоциации паров воды:
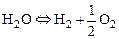 , (1.4.3)
, (1.4.3)
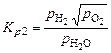 , (1.4.4)
, (1.4.4)
протекающих одновременно в смеси, будет наблюдаться их взаимное влияние. Совместное протекание этих реакций легче исследовать, если составить суммарную реакцию
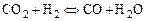 , (1.4.5)
, (1.4.5)
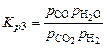 . (1.4.6)
. (1.4.6)
Константа равновесия суммарной реакции, называемой реакцией водяного пара, равна:
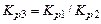 . (1.4.7)
. (1.4.7)
Особенностью этой реакции является то, что она проходит без изменения числа молей (объема). Следовательно, состав продуктов сгорания, если они образуются в соответствии с этой реакцией, не зависит от давления.
Уравнение реакции водяного пара используется при проведении расчетов равновесных состояний.
Константа равновесия 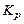 гетерогенных систем.Формулы (1.3.20) и (1.3.21) для констант равновесия
гетерогенных систем.Формулы (1.3.20) и (1.3.21) для констант равновесия 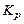 были введены для гомогенных химических систем, состоящих из газов.
были введены для гомогенных химических систем, состоящих из газов.
Рассмотрим теперь условия химического равновесия гетерогенных систем, состоящих из газов, твердых веществ и жидкостей. Примером реакции, протекающей в такой системе, является реакция сжигания графита Св атмосфере кислорода 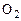 :
:
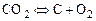 . (1.4.8)
. (1.4.8)
На основе современных представлений о механизме протекания таких реакций предполагается, что они проходят следующим образом.
Над твердыми и жидкими веществами гетерогенных систем в результате испарения и сублимации находятся насыщенные пары этих веществ. Эти пары имеют парциальные давления, зависящие только от температуры, и находятся в равновесном состоянии с веществами, из которых они образовались. Убыль пара в газообразной фазе, вступившего в химическую реакцию, будет пополняться дополнительным испарением жидкости или дополнительной сублимацией твердых тел. В результате этого парциальные давления насыщенных паров жидких и твердых тел будут, несмотря на реакцию, оставаться постоянными при постоянной температуре смеси. Так как в данном случае реакция протекает между газообразными веществами, то формулы (1.3.20) и (1.3.21) остаются справедливыми и для гетерогенных веществ.
В соответствии с изложенным реакцию (1.4.8) можно представить в виде
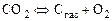 . (1.4.9)
. (1.4.9)
при этом константа равновесия будет равна:
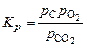 , (1.4.10)
, (1.4.10)
где давление 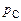 при постоянной температуре также будет оставаться постоянным.
при постоянной температуре также будет оставаться постоянным.
Константа равновесия 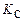 . Введем понятие объемно-моль-ной концентрации. Под объемно-мольной концентрацией i-го газа
. Введем понятие объемно-моль-ной концентрации. Под объемно-мольной концентрацией i-го газа 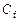 понимается число молей i-го газа в единице объема. Тогда
понимается число молей i-го газа в единице объема. Тогда
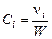 . (1.4.11)
. (1.4.11)
Концентрации 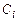 отдельных газов, образующих смесь, будут пропорциональны парциальным давлениям этих газов. Это утверждение следует из (1.2.7), (1.2.8), (1.1.7), (1.2.27). Так как
отдельных газов, образующих смесь, будут пропорциональны парциальным давлениям этих газов. Это утверждение следует из (1.2.7), (1.2.8), (1.1.7), (1.2.27). Так как 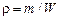 , то уравнение состояния для i-й газовой компоненты имеет вид
, то уравнение состояния для i-й газовой компоненты имеет вид
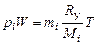 . (1.4.12)
. (1.4.12)
Учитывая соотношение (1.4.11) и равенство 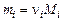 , получим
, получим
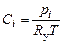 . (1.4.13)
. (1.4.13)
Формула (1.4.13) показывает, что объемно-мольная концентрация газа пропорциональна его парциальному давлению.
Константа равновесия 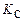 , устанавливающая связь объемно-мольных концентраций компонентов, участвующих в химической реакции, может быть выражена через константу равновесия
, устанавливающая связь объемно-мольных концентраций компонентов, участвующих в химической реакции, может быть выражена через константу равновесия 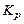 . Согласно формуле (1.4.13),
. Согласно формуле (1.4.13),
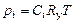 . (1.4.14)
. (1.4.14)
Подставляя значения парциальных давлений, связанных с концентрациями 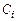 соотношением (1.4.14), в (1.3.20), получим
соотношением (1.4.14), в (1.3.20), получим
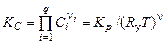 , (1.4.15)
, (1.4.15)
где 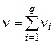 – суммарное количество молей газа в смеси.
– суммарное количество молей газа в смеси.
Диссоциация. Влияние давления на степень диссоциации. Распад химического соединения на более простые вещества, которыми в частном случае могут быть химические элементы, называется диссоциацией.
Исследуем влияние давления на степень диссоциации на примере двухатомного газа. Пусть это будет кислород. Реакция диссоциации кислорода записывается в виде
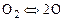 . (1.4.16)
. (1.4.16)
Обозначим через 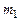 массу атомарного кислорода О,а через
массу атомарного кислорода О,а через 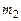 массу молекулярного кислорода
массу молекулярного кислорода 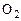 и примем, что суммарная масса равна единице:
и примем, что суммарная масса равна единице:
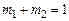 . (1.4.17)
. (1.4.17)
Степень диссоциации bопределяется как отношение
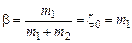 . (1.4.18)
. (1.4.18)
Далее воспользуемся соотношением
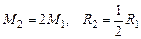 . (1.4.19)
. (1.4.19)
Тогда давление смеси будет равно:
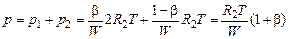 . (1.4.20)
. (1.4.20)
В соответствии с законом действующих масс,
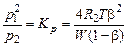 . (1.4.21)
. (1.4.21)
Подставляя в последнее соотношение давление смеси
(см. (1.4.20)), получим
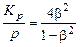 . (1.4.22)
. (1.4.22)
Формула (1.4.22) показывает, что с ростом давления степень диссоциации b уменьшается. В табл. 1.1 приведены значения b для реакции диссоциации кислорода при различных давлениях смеси, которые это иллюстрируют.
Т а б л и ц а 1.1
| T=3000 K | T=3500 K | ||
| р, ата | b | р, ата | b |
| 0.060 | 0.251 | ||
| 0.019 | 0.082 | ||
| 0.006 | 0.026 |
В общем случае справедливы утверждения:
· в реакциях, происходящих с увеличением числа молей, при возрастании давления степень диссоциации уменьшается;
· в реакциях, происходящих без изменения числа молей, степень диссоциации не зависит от давления.
Дата добавления: 2018-11-25; просмотров: 745;
