Методы вывода и поиска решений в продукционных системах. Методы вывода на основе прямой и обратной цепочек.

При продукционном представлении область знаний представляется множеством продукционных правил если - тогда, а данные представляются множеством фактов о текущей ситуации.

Механизм вывода сопоставляет каждое правило, хранящееся в БЗ с фактами, содержащимися в БД. Когда часть правила если (условие) подходит факту, правило срабатывает и его часть тогда (действие) исполняется. Срабатывающее правило может изменить множество фактов путем добавления нового факта, как показано на рис.6.1. Буквы в БД и БЗ используются для представления ситуаций и понятий.

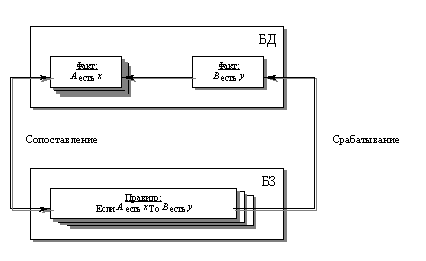
Рис.6.1. Цикл механизма вывода через процедуру «сопоставление – срабатывание»

Сопоставление частей если правил с фактами создает цепочку вывода. Цепочка вывода показывает как ЭС применяет правила для получения заключения. Для иллюстрации метода вывода на основе цепочки, рассмотрим простой пример.

Допустим, БД первоначально включает факты А,В,С,D и Е, а БЗ содержит только три правила:

Правило 1. Y&D → Z

Правило 2. X&B&E→Y

Правило 3. A→X

Цепочка вывода на рис. 6.2. показывает, как ЭС применяет правила для вывода факта Z.

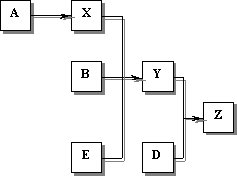
Рис.6.2. Пример цепочки вывода.

Сначала срабатывает Правило 3 для вывода нового факта Х изданного факта A. Тогда Правило 2 выполняется для вывода факта Y из первоначально фактов В и Е, а также уже известного факта Х. И наконец, Правило 1 применяет первоначально известный факт D и только что полученный факт Y для прихода и заключению Z.

ЭС может отразить свою цепочку вывода для объяснения, как было достигнуто отдельное решение; это является основной частью ее объяснительных способностей.

Механизм вывода должен решать, когда правила должны сработать. Существует два принципиальных способа, которыми правила могут быть выполнены. Один называется прямая цепочка (условно-выводимая), а другая обратная цепочка (целе-выводимая) [133].

Рассмотренный пример использует прямую цепочку вывода.

Продукционные системы, в которых сначала анализируется антецедентная часть (условия), имеют так называемую условно-выводимую архитектуру. Примером экспертной системы такой ар­хитектуры является META-DENDRAL.

Альтернативным типом архитектуры, которая достаточно час­то используется в экспертных системах, являются целе-выводимые (действие-выводимые или консеквент-выводимые) продукци­онные системы. Например, правило вида

А&В&С→D

может быть интерпретировано, как

«Логическая конъюнкция А, В и С влечет D» или

«Чтобы доказать D, необходимо установить А, В, С».

В последнем случае цель должна быть достигнута дедуктивным выводом. Для этого исследуются консеквенты правил для нахож­дения такого правила, которое позволило бы достичь цели. Когда такое правило найдено, проверяются на истинность все его усло­вия. Если условия истинны, продукция активируется. В против­ном случае продолжается поиск подходящей продукции.

Рассмотрим упрощенный пример продукционной системы с консеквент-выводимой архитектурой. Буквами здесь обозначе­ны элементы БД и они считаются истинными, если содержатся в ней.

БД: АF

Правило 1: A&B&C→D

Правило 2: D&F→G

Правило 3:A&J→G

Правило 4: В→С

Правило 5: F→B

Правило 6: L→J

Правило 7: G→H

Предположим, цель состоит в том, чтобы вывести истинность Н. В первую очередь проверяется, находится ли Н в БД? Так как в данном случае это не так, то система пытается вывести истин­ность Н, используя правила, имеющие Н в правой части. Таким является правило 7. Теперь система пытается вывести истинность G, так как истинность последнего влечет за собой истинность Н. Снова проверяется БД: в БД нет G, следовательно, организуется полек правила, содержащего G в правой части. Таких правил несколько (два или три). В качестве стратегии «разрешения кон­фликта» будем считать, что правила упорядочены по приоритету, причем правилу с наименьшим номером соответствует больший приоритет.

В данном случае выбирается правило 2, поэтому целью теперь становится вывести истинность D и F. Для этого достаточно по­казать, что А - истинно (так как находится в БД), В - истинно (согласно правилу 5), С - истинно (согласно правилу 4). Так как истинность D и F доказана, то из правила 2 следует истинность G, а из истинности G - следует истинность Н (правило 7). Таким образом цель достигнута. Элементы, истинность которых доказана, добавляются в БД. В данном случае это - элементы Н, G, D, С. В. Примерами целе-выводимой архитектуры является MYCIN.