Исчисление предикатов

Классическим механизмом представления знаний в системах является исчисление предикатов (использовалось уже в 50-х годах в исследованиях по ИИ). В системах, основанных на исчислении предикатов, знания представляются с помощью перевода утверждений об объектах некоторой предметной области в формулы логики предикатов и добавления их как аксиом в систему. Рассмотрим основные положения логики предикатов.

Пусть имеется некоторое множество объектов, называемых предметной областью М. Знаки, обозначающие элементы этого множества, называют предметными константами, а знак, обозначающий произвольный элемент этого множества, – предметной переменной. Терм – это всякая предметная область или предметная константа если f – функциональная n-местная буква, и t₁, t_2,…,t _n – термы, то f(t_1,…,t _n) есть терм.

Выражение Р (x₁,x₂,…,x_n), где x_i, i= 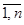- предметные переменные, а Р принимает значения 0 и 1, называется логической функцией или предикатом. Переменные принимают значения из произвольного конечного и бесконечного множества М.

Предикатом или логической функцией называется функция от любого числа аргументов, принимающая истинные значения 1 и 0. Если в данном выражении заменить x_i на y_i, где y_i – предметные константы, то получим элементарную формулу, т.е. предикатные буквы применимы также и к предметным константам. Элементарные формулы иногда называют атомными. Из элементарных формул с помощью логических связок Ú (или), Ù (и), Ø (отрицание), ® (импликация) строят предметные формулы (иногда их называют правильно построенными формулами - ППФ). ППФ – один из важных классов выражений в исчислении предикатов. Кроме логических связок в рассмотрение вводят кванторы общности " или существования $.

Если Р – предметная формула, а х – предметная переменная, то выражения

"х Р(х) и $ х Р(х) также считаются предметными формулами. В логике предикатов для компактной записи высказываний типа: “для любого х истинно Р(х)” и “существует такое х, для которого истинно Р(х)” вводится две новые дополнительные операции: кантор общности " и квантор существования $. Посредством этих операций приведенные выше высказывания записываются в виде "х Р(х) и $ х Р(х). Выражение "х Р(х) обозначает высказывание истинное, когда Р(х) истинно при всех х Î М и ложно в противном случае.

Если P(x) в действительности не зависит от x, то выражения "х Р(х) и $ х Р(х) обозначают то же, что и P(x).

Конкретное вхождение переменной x в формулу P называется связанным, если оно либо непосредственно следует за каким-либо квантором, либо содержится в области действия некоторого квантора " или $. Вхождение переменной является свободным, если оно не является связанным. В выражении "x P(x,y) x- связанная, y- связанная.

Связанной переменной называется переменная, если в P имеется вхождение этой переменной.

Использование обоих кванторов не является обязательным. Рассмотрим выражение 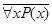, оно обозначает высказывание « 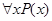ложно», равносильное высказыванию «существует элемент x, для которого P(x)» ложно или, что тоже «существует элемент x, для которого 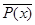истинно». Следовательно, 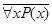равносильно выражению : = .

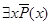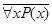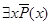Под интерпретацией предикатных формул понимают конкретизацию предметной области, соответствующей данной предметной формуле, и установке соответствия между символами, входящими в предмет, и элементами (а также функциями и отношениями), определяемыми в данной предметной области.