Операции с нечеткими множествами.

Приведем некоторые из основных операций, которые можно осуществлять над нечетким множествами.

1. Дополнение нечеткого множества А обозначается символом 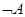и определяется следующим образом:

(5.15)

Операция дополнения соответствует логическому отрицанию. Например, если А - название нечеткого множества, то «не А» понимается как 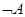(см. пример ниже).

2. Объединение нечетких множеств А и В обозначается А+В (или АÈВ) и определяется:

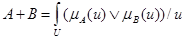(5.16)

Объединение соответствует логической связке «или». Например, если А и В – названия нечетких множеств, то запись «А или В» понимается как А+В.

При определении степени принадлежности элементов u новому нечеткому множеству, выбирают большее из .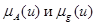

Замечание:следует иметь в виде, что логическая связка Ú в данном контексте означает по определению max (т.е. 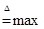); Ù означает min (т.е. ).

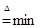3. Пересечение А и В обозначаются АÇВ и определяется следующим образом:

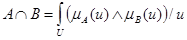(5.17)

Пересечение соответствует логической связке «u», т.е.

А иВ=АÇВ (5.18)

При определении степени принадлежности элементов u новому нечеткому множеству, выбирают меньшее из 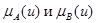(см. замечание выше).

4. Произведение А и В обозначается АВ и определяется формулой

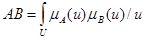(5.19)

если 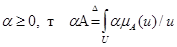(5.20)

Пример 5.5. Если

U=1+2+…+10

A=0.8/3+1/5+0.6/6 (5.21)

B=0.7/3+1/4+0.5/6,

То ØА=1/1+1/2+0.2/3+1/4+0.4/6+1/7+1/8+1/9+1/10

А+В=0.8/3+1/4+1/5+0.6/6

АÇВ=0.7/3+0.5/6 (берется min из двух значений m) (5.22)

АВ=0.56/3+0.3/6

0.4А=0.32/3+0.4/5+0.24/6

5. Декартово произведение нечетких множеств А₁, …, А_n универсальных множеств U₁,…,U_n соответственно обозначается А₁´…´А_n и определяется как нечеткое подмножество множества U₁´…´U_n с функцией принадлежности.

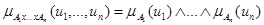(5.23)

т.о. 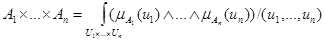(5.24)

Пример 5.6. Если

U₁=U₂ =3+5+7

A₁=0.5/3+1/5+0.6/7

A₂=1/3+0.6/5, то

A₁´A₂=0.5/3.3+1/5.3+0.6/7.6+0.5/3.5+0.6/5.5+0.6/7.5