Основные определения нечетких множеств.

Рассмотрим универсальное множество U={u}.

Нечетким подмножеством A на множестве U называется совокупность пар

A={<m_a (u), u>} (5.1)

Где m_a: U® [0,1] – отображение множества U в единичный отрезок [0,1], называемое функцией принадлежности нечеткого подмножества A.

Значение функции принадлежности m_a (u) для элемента uÎU будем называть степенью принадлежности. Для упрощения записи будем считать, что выражению (5.1) эквивалентны выражения

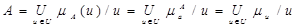
Переменная u называется базовой.

Интерпретацией степени принадлежности m_A(u) является субъективная мера того, насколько элемент uÎU соответствует понятию, смысл которого формализуется нечетким множеством A.

Таким образом, нечеткое множество А области рассуждений U характеризуются функцией принадлежности.

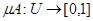, которая каждому элементу u множества U ставит в соответсвие число 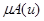из отрезка [0,1], описывающее степень принадлежности элемента u подмножеству А.

Носителем нечеткого подмножества (далее: множества) Ф называется множество таких элементов U, для которых 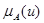положительна.

Точкой перехода А называется такой элемент множества U, степень принадлежности которого множеству A равна 0,5.

Пример 5.1: Рассмотрим нечеткое множество A₃, соответствующее нечеткому понятию “небольшой запас деталей на складе”. Носителем данного нечеткого множества является конечное множество:

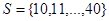, каждый элемент которого представляет собой определенное количество деталей.

A₃={0.05/10; 0.1/11; 0.2/12; 0.3/13; 0.4/14; 0.5/15;

0.7/16; 0.8/19; 1.0/20; … 1.0/33; 0.9/34; 0.8/35;

0.6/36; 0.4/37; 0.3/38; 0.2/39; 0.1/40}

Отсюда следует, что в решаемой задаче управления запасами для конкретного ЛПР понятию “небольшой запас деталей на складе” полностью соответствует запас объемом от 20 до 33 деталей, в меньшей степени – запасы от 10 до 19 и от 34 до 40 деталей. Запас объемом меньше 10 и больше 40 деталей понятием “небольшой” охарактеризован быть не может.

Далее для краткости нечеткое подмножество А множества U будем называть нечетким множеством А.

Одноточечным нечетким множеством называется множество, носитель которого состоит из единственной точки. Если А – одноточечное нечеткое множество, носителем которого является точка u, то записывается это как:

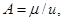(5.2)

Где m - степень принадлежности u множеству А. Определенное (четкое) одноточечное множество обозначают через 1/ u.

Нечеткое множество можно рассматривать как объединение составляющих его одноточечных множеств. Имея это ввиду, множество А можно представить в следующем виде:

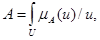(5.3)

где символ ∫(интегрирование) обозначает операцию объединения одноточечных нечетких множеств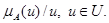

Если носитель А состоит из конечного числа элементов, то интегрирование в (5.3.) можно заменить суммированием:

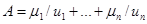(5.4)

или

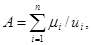(5.5)

где число 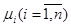- степень принадлежности элемента U_i множеству А. Знак плюс в (5.4) обозначает объединение, а не арифметическое суммирование.

Пример 5.2. Если универсальное множество состоит из чисел от 1 до 10, т.е.

U=1+…+10, (5.6)

То нечеткое множество А множества U, описываемое понятием «несколько» можно определить в виде

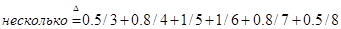(5.7)

(символ 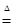обозначает равенство по определению).

Пример 5.3. Если U интервал с элементами [0,100] и 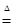возраст, то нечеткие подмножества, описываемые понятиями «молодой» и «старый» можно представить в виде (здесь и ниже нечеткое множество отождествляться с понятием, которое его описывает).

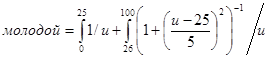(5.8)

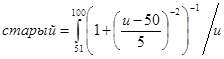(5.9)

см. рис. 5.5.

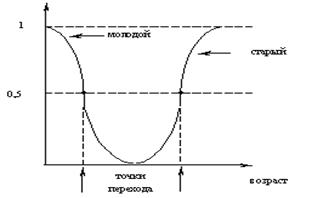
Рис. 5.5. Графическое представление лингвистических понятий «молодой» и «старый».

Степень принадлежности к нечеткому множеству может сама представлять собой нечеткое множество.

Пример 5.4. Если есть множество

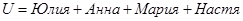(5.10)

и А - нечеткое множество «привлекательная», то можно написать

«привлекательная»=средне/Юлия+мало/Анна+сильно/Мария+мало/Настя.

Нечеткие степени принадлежности «мало», «средне» и «сильно» являются при этом нечеткими подмножествами полного множества V, определяемого следующим образом:

V=0+0.1+0.2+…+0.9+1 (5.11)

Сами эти подмножества определяются так:

мало=0.5/0.2+0.7/0.3+1/0.4+0.7/0.5+0.5/0.6 (5.12)

средне=0.5/0.4+0.7/0.5+1/0.6+0.7/0.7+0.5/0.8 (5.13)

сильно=0.5/0.7+0.7/0.8+0.9/0.9+1/1 (5.14)