От биологических сетей к ИНС
Современные компьютеры превосходят человека по способности производить числовые и символьные вычисления. Однако человек может без усилий решать сложные задачи восприятия внешних данных (например, узнавание человека в толпе только по его промелькнувшему лицу) с такой скоростью и точностью, что мощнейший в мире компьютер будет ему уступать. В чем причина столь значительного различия в их производительности? Архитектура биологической нейронной системы совершенно не похожа на архитектуру машины фон Неймана (Таблица 5.1), существенно влияет на типы функций, которые более эффективно исполняются каждой моделью.
Таблица 5.1.
Машина фон Неймана по сравнению с биологической нейронной системой.
| Машина фон Неймана | Биологическая нейронная система | |
| Процессор | Сложный | Простой |
| Высокоскоростной | Низкоскоростной | |
| Один или несколько | Большое количество | |
| Память | Отделена от процессора | Интегрирована в процессор |
| Локализована | Распределенная | |
| Адресация не по содержанию | Адресация по содержанию | |
| Вычисления | Централизованные | Распределенные |
| Последовательные | Параллельные | |
| Хранимые программы | Самообучение | |
| Надежность | Высокая уязвимость | Живучесть |
| Специализация | Численные и символьные операции | Проблемы восприятия |
| Среда функционирования | Строго определенная | Плохо определенная |
| Строго ограниченная | Без ограничений |
Подобно биологической нейронной системе ИНС является вычислительной системой с огромным числом параллельно функционирующих простых процессоров с множеством связей. Модели ИНС в некоторой степени воспроизводят "организационные" принципы, свойственные мозгу человека. Моделирование биологической нейронной системы с использованием ИНС может также способствовать лучшему пониманию биологических функций. Такие технологии производства, как VLSI (сверхвысокий уровень интеграции) и оптические аппаратные средства, делают возможным подобное моделирование.
Глубокое изучение ИНС требует знания нейрофизиологии, когнителогии, психологии, физики (статистической механики), теории управления, теории вычислений, проблем искусственного интеллекта, статистики/математики, распознавания образов, компьютерного зрения, параллельных вычислений и аппаратных средств (цифровых/аналоговых/VLSI(Very-Large-Scale-Integration)/оптических). С другой стороны, ИНС также стимулируют эти дисциплины, обеспечивая их новыми инструментами и представлениями. Этот симбиоз жизненно необходим для исследований по нейронным сетям.
Представим некоторые проблемы, решаемые в контексте ИНС и представляющие интерес для ученых и инженеров, разрабатывающих ИСПР [103].
Классификация образов. Задача состоит в указании принадлежности входного образа (например, речевого сигнала или рукописного символа), представленного вектором признаков, одному или нескольким предварительно определенным классам. К известным приложениям относятся распознавание букв, распознавание речи, классификация сигнала электрокардиограммы, классификация клеток крови.
Кластеризация/категоризация. При решении задачи кластеризации, которая известна также как классификация образов "без учителя", отсутствует обучающая выборка с метками классов. Алгоритм кластеризации основан на подобии образов и размещает близкие образы в один кластер. Известны случаи применения кластеризации для извлечения знаний, сжатия данных и исследования свойств данных.
Аппроксимация функций. Предположим, что имеется обучающая выборка ((x1,y1), (x2,y2)..., (xn,yn)) (пары данных вход-выход), которая генерируется неизвестной функцией (x), искаженной шумом. Задача аппроксимации состоит в нахождении оценки неизвестной функции (x). Аппроксимация функций необходима при решении многочисленных инженерных и научных задач моделирования.
Предсказание/прогноз. Пусть заданы n дискретных отсчетов {y(t1), y(t2)..., y(tn)} в последовательные моменты времени t1, t2,..., tn . Задача состоит в предсказании значения y(tn+1) в некоторый будущий момент времени tn+1. Предсказание/прогноз имеют значительное влияние на принятие решений в бизнесе, науке и технике. Предсказание цен на фондовой бирже и прогноз погоды являются типичными приложениями техники предсказания/прогноза.
Оптимизация. Многочисленные проблемы в математике, статистике, технике, науке, медицине и экономике могут рассматриваться как проблемы оптимизации. Задачей алгоритма оптимизации является нахождение такого решения, которое удовлетворяет системе ограничений и максимизирует или минимизирует целевую функцию.
Память, адресуемая по содержанию. В модели вычислений фон Неймана обращение к памяти доступно только посредством адреса, который не зависит от содержания памяти. Более того, если допущена ошибка в вычислении адреса, то может быть найдена совершенно иная информация. Ассоциативная память, или память, адресуемая по содержанию, доступна по указанию заданного содержания. Содержимое памяти может быть вызвано даже по частичному входу или искаженному содержанию. Ассоциативная память чрезвычайно желательна при создании мультимедийных информационных баз данных.
Управление. Рассмотрим динамическую систему, заданную совокупностью {u(t), y(t)}, где u(t) является входным управляющим воздействием, а y(t) - выходом системы в момент времени t. В системах управления с эталонной моделью целью управления является расчет такого входного воздействия u(t), при котором система следует по желаемой траектории, диктуемой эталонной моделью. Примером является оптимальное управление двигателем.
Краткий исторический обзор.
Исследования в области ИНС пережили три периода активизации. Первый пик в 40-х годах обусловлен пионерской работой МакКаллока и Пейперта [33]. Второй возник в 60-х благодаря теореме сходимости перцептрона Розенблатта [54] и работе Минского и Пейперта [37], указавшей ограниченные возможности простейшего перцептрона. Результаты Минского и Пейперта погасили энтузиазм большинства исследователей, особенно тех, кто работал в области вычислительных наук. Возникшее в исследованиях по нейронным сетям затишье продлилось почти 20 лет. С начала 80-х годов ИНС вновь привлекли интерес исследователей, что связано с энергетическим подходом Хопфилда [101] и алгоритмом обратного распространения для обучения многослойного перцептрона (многослойные сети прямого распространения), впервые предложенного Вербосом и независимо разработанного рядом других авторов. Алгоритм получил известность благодаря Румельхарту [123].
Биологические нейронные сети
Нейрон (нервная клетка) является особой биологической клеткой, которая обрабатывает информацию (рис. 5.8). Она состоит из тела клетки (cell body), или сомы (soma), и двух типов внешних древоподобных ветвей: аксона (axon) и дендритов (dendrites), Тело клетки включает ядро (nucleus), которое содержит информацию о наследственных свойствах, и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает сигнал (импульсы) от других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль аксона (передатчик), который в конце разветвляется на волокна (strands). На окончаниях этих волокон находятся синапсы (synapses).
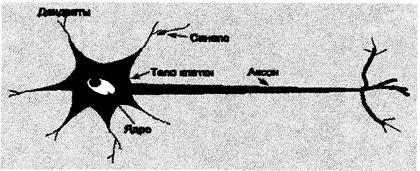
Рис. 5.8. Схема биологического нейрона.
Синапс является элементарной структурой и функциональным узлом между двумя нейронами
(волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического
окончания, высвобождаются определенные химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую щель, возбуждая или затормаживая, в зависимости от типа синапса, способность нейрона-приемника генерировать электрические импульсы. Результативность синапса может настраиваться проходящими через него сигналами, так что синапсы могут обучаться в зависимости от
активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как
память, которая, возможно, ответственна за память человека.
Кора головного мозга человека является протяженной, образованной нейронами поверхностью толщиной от 2 до 3 мм с площадью около 2200 см2, что вдвое превышает площадь поверхности
стандартной клавиатуры, Кора головного мозга содержит около 1011 нейронов, что приблизительно равно числу звезд Млечного пути [12]. Каждый нейрон связан с 103 - 104 другими нейронами. В целом мозг человека содержит приблизительно от 1014 до 1015 взаимосвязей. Нейроны взаимодействуют посредством короткой серии импульсов, как правило, продолжительностью несколько мсек. Сообщение передается посредством частотно-импульсной модуляции. Частота может изменяться от нескольких единиц до сотен герц, что в миллион раз медленнее, чем самые быстродействующие переключательные электронные схемы. Тем не менее, сложные решения по восприятию информации, как, например, распознавание лица, человек принимает за несколько сотен мс. Эти решения онтролируются сетью нейронов, которые имеют скорость выполнения операций всего несколько мс. Это означает, что вычисления требуют не более 100 последовательных стадий. Другими словами, для таких сложных задач мозг "запускает" параллельные программы, содержащие около 100 шагов. Это известно как правило ста шагов. Рассуждая аналогичным образом, можно обнаружить, что количество информации, посылаемое от одного нейрона другому, должно быть очень маленьким (несколько бит). Отсюда следует, что основная информация не передается непосредственно, а захватывается и распределяется в связях между нейронами. Этим объясняется такое название, как коннекционистская модель, применяемое к ИНС.
Основные понятия
Модель технического нейрона
МакКаллок и Питтс предложили использовать бинарный пороговый элемент в качестве
модели искусственного нейрона. Этот математический нейрон вычисляет взвешенную сумму n входных сигналов xj, j = 1, 2... n, и формирует на выходе сигнал величины 1, если эта сумма превышает определенный порог u, и 0 - в противном случае. Часто удобно рассматривать u как весовой коэффициент, связанный с постоянным входом x0=1. Положительные веса соответствуют возбуждающим связям, а отрицательные – тормозным. МакКаллок и Питтс доказали, что при соответствующим образом подобранных весах совокупность параллельно функционирующих нейронов подобного типа способна выполнять универсальные вычисления. Здесь наблюдается определенная аналогия с биологическим нейроном: передачу сигнала и взаимосвязи имитируют аксоны и дендриты, веса связей соответствуют синапсам, а пороговая функция отражает активность сомы.
ИНС представляет собой модель, прототипом которой является биологическая нейронная сеть. Сегодняшние нейронные вычисления используют очень ограниченное множество понятий биологических нейронных сетей (см. табл.5.2.).
Таблица 5.2.
Некоторые аналогии и отношения между биологическими и искусственными нейронными сетями.
| Биологические | Искусственные |
| Сома Дендриты Аксон Синапс Много нейронов (109) | Узел Вход Выход Вес Немного нейронов (от десятка до сотни тысяч) |
Понятия используются для осуществления программной имитации массированных параллельных процессов, которые включают обрабатывающие элементы (также называемые искусственными нейронами), взаимосвязанными в архитектуру нейронной сети. Искусственный нейрон получает входные сигналы, являющиеся аналогами электрохимических импульсов, которые дендриты биологических нейронов получают от других нейронов.
Входные сигналы искусственного нейрона соответствуют сигналам, посылаемым от биологического нейрона через его аксон. Эти искусственные сигналы могут быть изменены таким же образом, как физические изменения происходят в синапсах.
Важно признать, что ИНС были первоначально предложены как способ моделирования деятельности человеческого мозга. Человеческий мозг имеет намного большую сложность, чем модель может выразить. Несмотря на обширные исследования в нейробиологии и физиологии, остаются важные вопросы о том, как работают мозг и разум человека. Это только одна причина, почему нейронные вычислительные модели не очень сходны с реальными биологическими системами. Тем не менее, исследования и разработки в области ИНС производят интересные и полезные системы, которые заимствуют некоторые черты.
Архитектура нейронной сети.
ИНС состоит из искусственных нейронов (или обрабатывающих элементов), организованных различными путями для формирования структуры сети.
На рис.5.9. представлена схема трех взаимосвязанных искусственных нейронов.
Каждый из нейронов получает входные сигналы, обрабатывает их и выдает простой выходной сигнал. Этот процесс показан на рис.5.10. Входным сигналом могут быть необработанные данные или выходные сигналы других нейронов. Выходной сигнал может быть конечным результатом или он может быть входным сигналом другого нейрона.
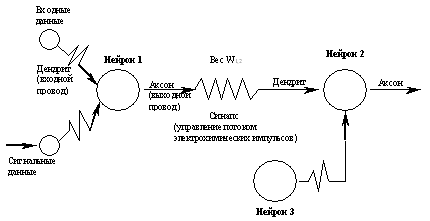
Рис.5.9. Три взаимосвязанных искусственных нейрона
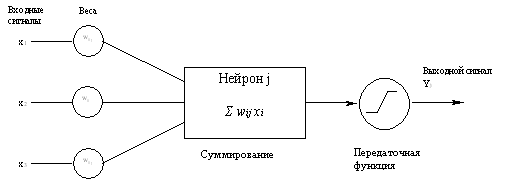
Рис.5.10. Обработка информации в искусственном нейроне
Каждая ИНС состоит из набора нейронов, которые сгруппированы по слоям. Типичная структура ИНС показана на рис.5.11. Здесь представлены три слоя: входной, промежуточный (называемый скрытым слоем) и выходной. Между входным и выходным слоями может быть размещено несколько скрытых слоев.
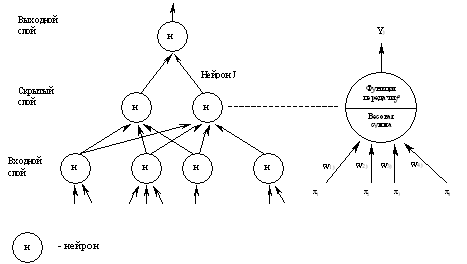 |
Рис.5.11. Нейронная сеть с одним скрытым слоем
Как и биологические нейронные сети, ИНС могут быть организованы несколькими различными способами (топологическими или архитектурными), т.е. нейроны могут быть взаимосвязаны различными способами. Поэтому ИНС проявляются в различных конфигурациях.
При обработке информации, многие обрабатывающие элементы выполняют свои вычисления одновременно. Эта параллельная обработка имеет сходство с тем, как работает мозг, и отличается от последовательной обработки при традиционных вычислениях.
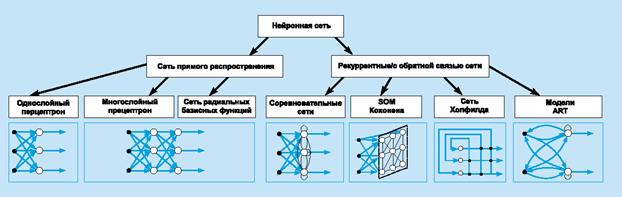
ИНС может рассматриваться как направленный граф со взвешенными связями, в котором искусственные нейроны являются узлами. По архитектуре связей ИНС могут быть сгруппированы в два класса (рис. 5.12): сети прямого распространения, в которых графы не имеют петель, и рекуррентные сети, или сети с обратными связями.
Рис. 5.12Систематизация архитектур сетей прямого распространения и рекуррентных (с обратной связью).
В наиболее распространенном семействе сетей первого класса, называемых многослойным перцептроном, нейроны расположены слоями и имеют однонаправленные связи между слоями. На рис. 5.12 представлены типовые сети каждого класса. Сети прямого распространения являются статическими в том смысле, что на заданный вход они вырабатывают одну совокупность выходных значений, не зависящих от предыдущего состояния сети. Рекуррентные сети являются динамическими, так как в силу обратных связей в них модифицируются входы нейронов, что приводит к изменению состояния сети.
Обучение
Способность к обучению является фундаментальным свойством мозга. В контексте ИНС процесс обучения может рассматриваться как настройка архитектуры сети и весов связей для эффективного выполнения специальной задачи. Обычно нейронная сеть должна настроить веса связей по имеющейся обучающей выборке. Функционирование сети улучшается по мере итеративной настройки весовых коэффициентов. Свойство сети обучаться на примерах делает их более привлекательными по сравнению с системами, которые следуют определенной системе правил функционирования, сформулированной экспертами.
Для конструирования процесса обучения, прежде всего, необходимо иметь модель внешней среды, в которой функционирует нейронная сеть - знать доступную для сети информацию. Эта модель определяет парадигму обучения. Во-вторых, необходимо понять, как модифицировать весовые параметры сети - какие правила обучения управляют процессом настройки. Алгоритм обучения означает процедуру, в которой используются правила обучения для настройки весов.
Существуют три парадигмы обучения: "с учителем", "без учителя" (самообучение) и смешанная. В первом случае нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Веса настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам. Усиленный вариант обучения с учителем предполагает, что известна только критическая оценка правильности выхода нейронной сети, но не сами правильные значения выхода. Обучение без учителя не требует знания правильных ответов на каждый пример обучающей выборки. В этом случае раскрывается внутренняя структура данных или корреляции между образцами в системе данных, что позволяет распределить образцы по категориям. При смешанном обучении часть весов определяется посредством обучения с учителем, в то время как остальная получается с помощью самообучения.
Теория обучения рассматривает три фундаментальных свойства, связанных с обучением по примерам: емкость, сложность образцов и вычислительная сложность. Под емкостью понимается, сколько образцов может запомнить сеть, и какие функции и границы принятия решений могут быть на ней сформированы. Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению. Слишком малое число примеров может вызвать "переобученность" сети, когда она хорошо функционирует на примерах обучающей выборки, но плохо - на тестовых примерах, подчиненных тому же статистическому распределению. Известны 4 основных типа правил обучения: коррекция по ошибке, машина Больцмана, правило Хебба и обучение методом соревнования.
1. Правило коррекции по ошибке. При обучении с учителем для каждого входного примера задан желаемый выход d. Реальный выход сети y может не совпадать с желаемым. Принцип коррекции по ошибке при обучении состоит в использовании сигнала (d-y) для модификации весов, обеспечивающей постепенное уменьшение ошибки. Обучение имеет место только в случае, когда перцептрон ошибается. Известны различные модификации этого алгоритма обучения.
2. Обучение Больцмана. Представляет собой стохастическое правило обучения, которое следует из информационных теоретических и термодинамических принципов. Целью обучения Больцмана является такая настройка весовых коэффициентов, при которой состояния видимых нейронов удовлетворяют желаемому распределению вероятностей. Обучение Больцмана может рассматриваться как специальный случай коррекции по ошибке, в котором под ошибкой понимается расхождение корреляций состояний в двух режимах .
3. Правило Хебба. Самым старым обучающим правилом является постулат обучения Хебба [98]. Хебб опирался на следующие нейрофизиологические наблюдения: если нейроны с обеих сторон синапса активизируются одновременно и регулярно, то сила синаптической связи возрастает. Важной особенностью этого правила является то, что изменение синаптического веса зависит только от активности нейронов, которые связаны данным синапсом. Это существенно упрощает цепи обучения в реализации VLSI.
4. Обучение методом соревнования. В отличие от обучения Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, при соревновательном обучении выходные нейроны соревнуются между собой за активизацию. Это явление известно как правило "победитель берет все". Подобное обучение имеет место в биологических нейронных сетях. Обучение посредством соревнования позволяет кластеризовать входные данные: подобные примеры группируются сетью в соответствии с корреляциями и представляются одним элементом.
При обучении модифицируются только веса "победившего" нейрона. Эффект этого правила достигается за счет такого изменения сохраненного в сети образца (вектора весов связей победившего нейрона), при котором он становится чуть ближе ко входному параметру.
Дата добавления: 2017-02-20; просмотров: 670;
