Нечеткие отношения.

Нечеткое отношение R: X®Y представляет собой нечеткое множество декартова произведения X´Y. R следующим образом описывается с помощью функции принадлежности двух переменных:

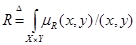(5.25)

Нечетким отношением на множестве X´Y называется совокупность пар

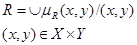(5.26)

где 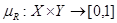- функция принадлежности нечеткого отношения R, имеющая тот же смысл, что и функция принадлежности нечеткого множества.

Вообще n- арное отношение есть нечеткое подмножество декартова произведения X₁´X₂´…´X_n, причем

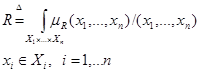(5.27)

Примеры нечетких отношений:

«X примерно равен Y»,

«X значительно больше Y»,

«А существенно предпочтительнее В».

Пример 5.7. Предположим, что X={Юрий, Сергей}, Y={Максим, Михаил}.

Тогда бинарное нечеткое отношение «сходства» между элементами множеств X и Y можно записать в виде

сходство=0.8/(Юрий,Максим)+0.6/(Юрий,Михаил)+0.2/(Сергей,Максим)+0.9/(Сергей, Михаил).

Помимо этого, данное отношение можно представить в виде матрицы отношений.

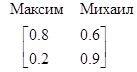(5.28)

В которой (i,j)-й элемент равен значению функции 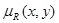для i-го значения x и j-го значения y.

Если R – отношение X®Y (или, что то же самое, отношение в X´Y), а S – отношение Y®Z, то композицией R и S является нечеткое отношение X®Z, обозначаемое R° S и определяемое формулой

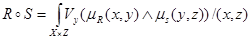(5.29)

где ° - знак композиции, знаки Ú и Ù обозначают соответственно max и min, V_y – верхняя грань по области значений у.

Здесь (5.29) является композицией отношений.

Выражение (5.29) определяет максминное произведение R и S.

Так, для действительных чисел а и b:

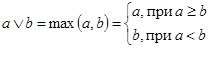(5.30)

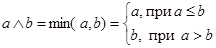(5.31)

Если X,Y,Z – конечные множества, то матрица отношения R° S есть максминное произведение матриц отношений R и S. В максминном произведении матриц вместо операции сложения и умножения используются операции Ú и Ù соответственно.

Пример максминного произведения

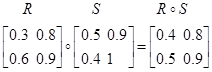(5.32)

Здесь количество строк должно равняться количеству столбцов. Строка умножается на столбец и берется максимальное значение из минимальных значений пар.