Процесс стандартизации.
Любую ППФ исчисления предикатов можно представить в виде предложения, применяя к ней последовательность простых операций. Задача состоит в том, чтобы показать, как придать произвольной ППФ форму предложения. Этот процесс (преобразования ППФ в форму предложения) состоит из следующих этапов:
1. Исключение знаков импликации. В форме предложения в исчислении предикатов явно используются лишь связки Ú и Ø. Знак импликации можно исключить в исходном утверждении вместо A®B ØA \/ B.
2. Уменьшение области действия знаков отрицания. Необходимо, чтобы знак отрицания Ø применялся не более чем к одной предикатной букве.
3. Стандартизация переменных, при которой осуществляется переименование переменных с тем, чтобы каждый квантор имел свою переменную. Так, вместо ("x){P(x) ® ($x)Q(x)} следует написать ("x){P(x) ® ($y)Q(y)}.
В области действия любого квантора переменная, связываемая им, является “немой” переменной. По этому везде в области действия квантора ее можно заменить другой переменной, а это не приведет к изменению значения истинности ППФ. Стандартизация переменных в ППФ означает переименование “немых ” переменных, с тем чтобы каждый квантор имел собственную немую переменную.
1. Исключение кванторов существования. Рассмотрим ППФ ("y$x)P(x,y), которую можно интерпретировать, например, так: для всех y существует такой x (возможно, зависящий от y), что x больше y. Заметим, что так как квантор существования ($x) находится внутри области действия квантора общности ("y), допускается, что значение x может зависеть от значения y в x. Пусть эта зависимость определяется явно с помощью некоторой функции g(y), отражающей каждое значение у в х, который «существует». Такая функция называется функцией Сколема. Если вместо x, который “существует”, взять функцию Сколема, то можно исключить квантор существования: ("y) P(g(y),y). Общее правило исключения из ППФ квантора существования состоит в замене в ней всюду переменной, относящейся к квантору существования, функцией Сколема, аргументами которой служат переменные, относящиеся к тем кванторам общности, области действия которых охватывают области действия исключамого квантора существования.
Функциональные буквы для функций Сколема должны быть “новыми”, в том смысле, что они не должны совпадать с теми буквами, которые уже имеются в ППФ. Если исключаемый квантор существования не принадлежит области действия ни одного из кванторов всеобщности, то функция Сколема не содержит аргументов, т.е. является постой константой: так ППФ ($x)P(x) превращается в P(a), где а - константа, про которую известно, что она существует. Чтобы исключить все переменные, относящиеся к кванторам существования, надо применить описанную ранее процедуру по очереди к каждой переменной.
Приведение к предваренной нормальной форме (ПНФ).На этом этапе уже не осталось кванторов существования, а каждый квантор общности имеет свою переменную. Теперь можно перенести все кванторы общности (") в начало ППФ и считать областью действия каждого квантора часть ППФ. Про полученную таким образом ППФ говорят, что она имеет предваренную нормальную форму (ПНФ). ППФ в ПНФ состоит из цепочки кванторов, называемой префиксом, и расположенной за ней формулы, не содержащей кванторов, называемой матрицей.
3. Приведение матрицы к конъюнктивной нормальной форме (КНФ). Любую матрицу можно представить в виде конъюнкций конечного множества дизъюнкций предикатов и (или) их отрицаний. Говорят, что такая матрица имеет КНФ. Заменить AÚ{BÙC} на {AÚB}Ù{AÚC}.
4. Исключение кванторов общности. Так как все переменные ППФ должны быть связанными, то все оставшиеся на этом этапе переменные относятся к " (общности). Так как порядок расположения кванторов общности несущественен, то эти кванторы можно явным образом не указывать, условившись, что все переменные в матрице относятся к кванторам общности. Таким образом остается лишь матрица в КНФ.
5. Исключение связок Ù,заменой AÙB двумя ППФ A и B. Результатом многократной замены будет конечное множество ППФ, каждая из которых представляет дизъюнкцию атомных формул и (или) их отрицаний. Атомную формулу или ее отрицание называют литерой (литералом), а ППФ, состоящую лишь из дизъюнкций литер, предложением. Этот процесс называется стандартизацией (т.е. преобразование формул в предложения).
Процесс, демонстрирующий, что некоторое множество F ППФ неудовлетворимо (невыполнимо), начинается с превращения каждой ППФ из множества F в предложение. В результате возникает некоторое множество S предложений. Можно показать, что если множество S неудовлетворимо, то неудовлетворимо и множество F.
Далее используется метод Эрбрана, т.е.к стандартной форме формулы применяют процедуры поиска опровержения, это делается для удобства реализации поиска, т.е. вместо доказательства общезначимости формулы доказывается, что отрицание формулы противоречиво. Возможно использование метода резолюций Робинсона [122].
Система представления знаний на основе исчисления предикатов имеет ряд достоинств:
1. Они достаточно хорошо исследованы как формальная система.
2. Существуют яcные правила, т.е. результаты операций над БЗ также достаточно ясно определены.
 |
Недостатками являются ограниченная выразимость, так как существует большое число факторов, которые тяжело или даже невозможно выразить средствами исчисления предикатов. В настоящее время аппаратное исчисление предикатов в чистом виде используется редко, однако основой большинства языков логического представления знаний, в частности, языка Пролог.
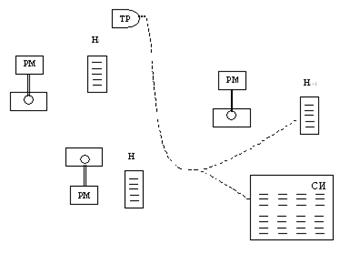
Рис.5.4. Схема роботизированного участка.
Пример:
Рассмотрим производственный роботизированный участок, оборудованный роботами манипуляторами (РМ), промежуточными накопителями готовых изделий (Hi), транспортным роботом (ТР) и складом изделий (СИ). См. рис. 5.4.
Задача ТР заключается в последовательном объезде промежуточных накопителей, сборе деталей (если они есть в накопителе) и транспортировке их на склад изделий. Если тележка ТР заполнена, то необходимо раньше заехать на склад изделий, разгрузиться там, а затем продолжить объезд накопителей.
Введем следующие предикаты:
A = пуст (накопитель)
B = пуста (тележка ТР)
C = освободить (накопитель)
D = перейти ((i+1)- й накопитель)
E = перевезти (на склад)
F = вернуться (i-й накопитель)
Тогда сформулированные правила можно записать так:
1. A®D
2.  A Ù B ® C Ù D
A Ù B ® C Ù D
3. 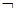 B® E Ù F
B® E Ù F
Переведем предикаты в форму предложений:
1. 
2. 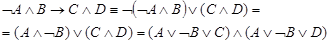
Последнюю запись можно представить в виде двух ППФ:
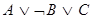 ,
, 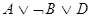
2. 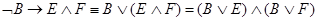 ,
,
что также разбивается на две ППФ
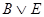 ,
, 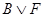
Теперь система правил будет иметь вид:
1. 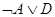
2. 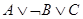 ,
, 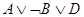
3. 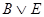 ,
, 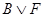
Дата добавления: 2017-02-20; просмотров: 579;
