Исчисление высказываний
Пусть интерпретация 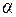 определена на всех высказывательных переменных, встречающихся в формулах множества
определена на всех высказывательных переменных, встречающихся в формулах множества 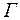 . Говорят, что
. Говорят, что 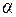 выполняет
выполняет 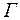 или
или 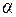 модель
модель 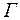 , если каждая формула
, если каждая формула 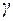 из
из 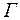 принимает значение «истина», при интерпретации
принимает значение «истина», при интерпретации 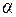 . Говорят, что
. Говорят, что 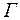 выполнимо, если
выполнимо, если 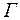 имеет модель. Если
имеет модель. Если 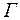 не выполнимо, то пишут
не выполнимо, то пишут 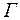 ÷=.
÷=.
Пусть 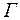 – множество формул логики высказываний, А – произвольная формула. Говорят, что множество
– множество формул логики высказываний, А – произвольная формула. Говорят, что множество 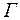 логически влечет формулу А, если любая модель
логически влечет формулу А, если любая модель 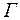 являются моделью для А и обозначается
являются моделью для А и обозначается 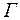 ÷= А.
÷= А.
Утверждение того, что некоторое высказывание (заключение) следует из других высказываний (посылок), называется аргументом. Аргумент часто представляют в виде:
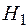
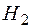
... гипотезы
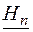
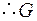 заключение
заключение
Аргумент называется правильным, если из множества гипотез логически следует заключение аргумента.
Второе правило исчисления высказываний: Modus Ponens.
Правило Modus Ponens: 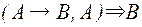 , т.е.
, т.е.
«Если 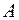 , то
, то 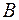 ; но
; но 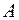 истинно, следовательно, истинно
истинно, следовательно, истинно 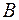 ».
».
Логика предикатов
С помощью формул логики высказываний можно описать структуру сложных высказываний. Для описания внутренней логической структуры простых высказываний (т.е. высказываний, не содержащих связок) используются другие средства, которые вместе с логикой высказываний образуют логику предикатов.
Чтобы яснее представить о какой логической структуре идет речь, рассмотрим пять высказываний:
1. 15 – нечетное число.
2. 8 – нечетное число.
3. 6 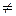 5.
5.
4. В Ярославле жителей больше, чем в Вязьме.
5. В Москве жителей больше, чем в любом другом городе России.
Все эти высказывания – простые и, следовательно, в логике высказываний изображаются одной буквой. Все, что о них можно сказать в этой логике, – это то, что высказывание (2) ложно, а остальные – истинны.
В то же время ясно, что между высказываниями (1) и (2) или между (4) и (5) сходства гораздо больше, чем между (1) и (5).
В высказываниях (1) и (2) речь идет о числах, которым приписывается одно и то же свойство – нечетность. В высказывании (3) утверждается наличие отношения неравенства между числами. В высказываниях (4) и (5) говорится о городах, относительно которых утверждается наличие некоторого отношения между ними – «иметь больше жителей».
Числа и города – это объекты. Множество объектов (целых чисел, городов России и т.д.), о которых делаются утверждения, называется предметной областью, а сами утверждения об отношениях между  объектами называются n-местными предикатами.
объектами называются n-местными предикатами.
С математической точки зрения:
n-местный предикат – это функция 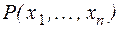 от
от 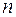 переменных, причем переменные принимают значения из предметной области, а функция
переменных, причем переменные принимают значения из предметной области, а функция 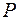 принимает два логических значения – истинно и ложно.
принимает два логических значения – истинно и ложно.
Нечетность – это одноместный предикат. Если его обозначить через 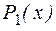 , тогда высказывания (1) и (2) запишутся как
, тогда высказывания (1) и (2) запишутся как 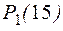 и
и 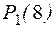 , т.е. как один и тот же предикат нечетности с разными значениями (15 и 8) переменной
, т.е. как один и тот же предикат нечетности с разными значениями (15 и 8) переменной 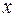 , взятыми из одной и той же предметной области целых чисел.
, взятыми из одной и той же предметной области целых чисел.
«Иметь больше жителей» – это двуместный предикат 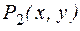 . Высказывание (4) можно записать как
. Высказывание (4) можно записать как 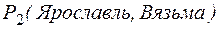 .
.
Неравенство – тоже двуместный предикат, для обозначения которого можно сохранить обычную запись: 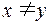 .
.
Таким образом, формулы вида 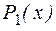 и
и 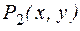 - это переменные высказывания, которые становятся истинными или ложными при подстановке вместо
- это переменные высказывания, которые становятся истинными или ложными при подстановке вместо 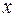 и
и 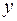 предметных констант – конкретных объектов из предметных областей.
предметных констант – конкретных объектов из предметных областей.
Кроме того, из предикатов можно получать конкретные высказывания, не содержащие предметных констант, а утверждающих нечто обо всей предметной области.
В естественном языке это делается с помощью оборотов «для всех 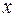 (т.е. для всех объектов) справедливо, что…» и «существует такой
(т.е. для всех объектов) справедливо, что…» и «существует такой 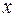 , что…».
, что…».
В языке формул логики предикатов этим оборотам соответствуют специальные знаки – кванторы: квантор общности 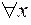 и квантор существования
и квантор существования 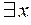 .
.
Присоединение квантора с переменной 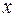 к предикатной формуле, содержащей
к предикатной формуле, содержащей 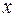 , называется навешиванием квантора на переменную
, называется навешиванием квантора на переменную 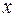 . Переменная
. Переменная 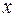 при этом называется связанной, вместо нее подставлять предметные константы уже нельзя.
при этом называется связанной, вместо нее подставлять предметные константы уже нельзя.
Например, формула 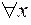
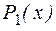 означает «для всех целых чисел справедливо то, что они нечетны» или, короче, «все целые числа – нечетны». Это – конкретное высказывание, которое ложно. Формула
означает «для всех целых чисел справедливо то, что они нечетны» или, короче, «все целые числа – нечетны». Это – конкретное высказывание, которое ложно. Формула 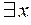
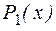 означает истинное высказывание «существуют нечетные целые числа».
означает истинное высказывание «существуют нечетные целые числа».
Если квантор навешивается на формулу с несколькими предметными переменными, то он уменьшает число свободных (несвязанных) переменных в этой формуле. Например, формула 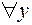
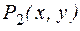 обозначает высказывание «в городе
обозначает высказывание «в городе 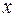 больше жителей, чем в любом городе
больше жителей, чем в любом городе 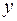 « и содержит одну свободную переменную
« и содержит одну свободную переменную 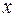 . Это высказывание ложно для любого
. Это высказывание ложно для любого 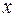 , потому что «любой город» подразумевает в том числе и
, потому что «любой город» подразумевает в том числе и 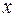 , но ни в каком городе не может быть больше жителей, чем в нем самом. «Шансы на истинность» имеет уточненное высказывание: «в городе
, но ни в каком городе не может быть больше жителей, чем в нем самом. «Шансы на истинность» имеет уточненное высказывание: «в городе 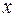 больше жителей, чем в любом другом городе
больше жителей, чем в любом другом городе 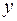 , не совпадающем с
, не совпадающем с 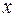 »:
»:
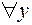
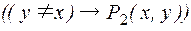 ,
,
в которой оба вхождения переменной 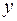 связаны квантором (с помощью скобок). Подстановка «Москва» вместо
связаны квантором (с помощью скобок). Подстановка «Москва» вместо 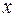 дает формулу, выражающую истинное высказывание (5).
дает формулу, выражающую истинное высказывание (5).
Как и в логике высказываний, в логике предикатов имеются эквивалентные соотношения, позволяющие преобразовывать предикатные формулы. Например,
- один квантор можно выразить через другой:
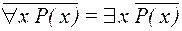 ,
, 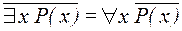 ,
,
- формулу, не содержащую переменную 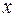 , можно вынести за пределы действия квантора, связывающего
, можно вынести за пределы действия квантора, связывающего 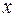 :
:
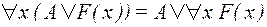 ;
; 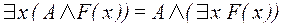 .
.
Однако, в целом, логику предикатов не удается представить в виде алгебры, столь же эффективной как алгебра логики (т.к. вычисление истинности предикатов, содержащих кванторы, в общем случае заключается в подстановке всех возможных значений предметных переменных, которых может быть бесконечное множество).
Поэтому логика предикатов организуется в виде исчисления предикатов, которое содержит аксиомы и правила вывода исчисления высказываний, а также дополнительные предикатные аксиомы и правила вывода.
В качестве аксиом обычно принимаются две формулы:
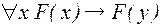 , (1)
, (1)
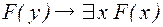 , (2)
, (2)
где 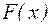 – любая предикатная формула, содержащая свободную переменную
– любая предикатная формула, содержащая свободную переменную 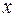 , а в качестве правил вывода – правила, вводящие кванторы:
, а в качестве правил вывода – правила, вводящие кванторы:
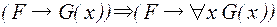 , (3)
, (3)
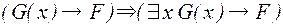 , (4)
, (4)
в этих правилах требуется, чтобы формула 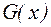 содержала свободную переменную
содержала свободную переменную 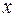 , а
, а 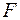 ее не содержала.
ее не содержала.
Пример.
Рассмотрим известнейший силлогизм, на протяжении двух тысячелетий переходящий из одних ученых трудов в другие:
Все люди смертны.
Дата добавления: 2018-09-24; просмотров: 650;
