Логика высказываний
Высказывание – это утверждение или повествовательное предложение, которое может быть либо истинным, либо ложным.
Значением истинного высказывания является «И» – истина, ложного – «ложь».
Повелительные («Войдите, пожалуйста»), вопросительные («Который час?») и бессмысленные предложения («Сумма пяти и восемнадцати»), в которых ничего не утверждается, не являются высказываниями.
Предметом логики является анализ различных логических связей и методы построения на их основе правильных логических рассуждений.
Способы построения новых высказываний из заданных с помощью логических связок и способы установления истинности высказываний, построенных таким образом, изучаются в логике высказываний.
Основные логические связки - это связки: и, или, не, если … то…, которые в логике высказываний имеют специальные названия и обозначения. Иногда к ним добавляют еще две связки либо …, либо …(или …, или …); если, и только если (тогда и только тогда).
Для одной и той же связки в разных источниках используются разные названия и обозначения, которые приведены в таблице 1.
Таблица 1
| Связка | Название | Обозначение | Высказывание, полученное с помощью связки | Математическая запись |
| 1. и | конъюнкция (или логическое умножение) | &, Ù, × | А и В | А & В, А Ù В, А × В, АВ |
| 2. или | дизъюнкция | Ú, + | А или В | А Ú В, А + В |
| 3. не | отрицание, инверсия | Ø, ¾ | не А | 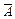 , ØА , ØА
|
| 4. если …, то … | импликация | ®, É | если А, то В (А влечетВ) | 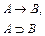
|
 5. либо …,
либо … 5. либо …,
либо …
| исключающее «или», неравнозначность | Å, D, ¹ | либо А, либо В | А Å В, А D В |
| 6. если и только если | эквивалентность, равнозначность | º, ~, « | А, если и только еслиВ | А º В, А ~ В |
В последней колонке табл. 1 записаны формулы, или выражения логики высказываний. С помощью букв А, В, С, ... обозначающих высказывания, связок и скобок можно построить разнообразные формулы.
Исследование свойств таких формул и способов установления их истинности и является основным предметом логики высказываний.
Существуют два подхода к построению логики высказываний, которые образуют два варианта этой логики: алгебру логики и исчисление высказываний.
Алгебра логики
Алгебра логики рассматривает логические формулы как алгебраические выражения, которые можно преобразовать по определенным правилам. Знаки операций обозначают логические операции (логические связки).
В формулах алгебры логики переменные – это высказывания.Они принимают только два значения – ложь и истина, которые обозначаются либо 0 и 1, либо Л и И, либо false и true.
Каждая формула задает логическую функцию: функцию от логических переменных, которая сама может принимать только два логических значения.
Таблица функций 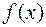 одной переменной:
одной переменной:
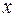
| Константа 0:
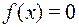
| Тождество:
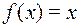
| Отрицание:
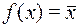
| Константа 1: 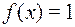
|
Таблица функций двух переменных 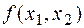 , соответствующих основным логическим связкам:
, соответствующих основным логическим связкам:
| Дизъюнкция | Конъюнкция | Импликация | Эквивалентность (равнозначность) | Неравнозначность (сложение по модулю 2) | Штрих Шеффера (НЕ – И) | Стрелка Пирса (НЕ – ИЛИ) | ||
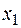
| 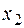
| 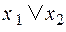
| 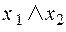
| 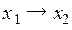
| 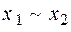
| 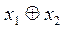
| 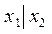
| 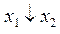
|
Значение любой логической формулы, содержащей знаки этих функций, на заданном наборе значений переменных можно вычислить, используя эти таблицы.
Интерпретацией формулы логики высказываний называется набор значений высказываний, входящих в нее.
Формула F называется тождественно истинной или тавтологией, если она принимает значение «истина» независимо от значений входящих в нее высказывательных переменных.Формула F называется выполнимой, если при некоторых значениях ее высказывательных переменных она принимает значение «истина». Такой набор значений высказывательных переменных называется моделью формулы F.
Дата добавления: 2018-09-24; просмотров: 1121;
